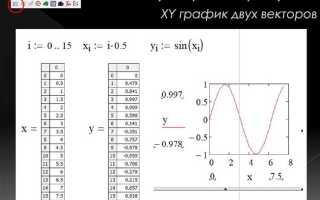
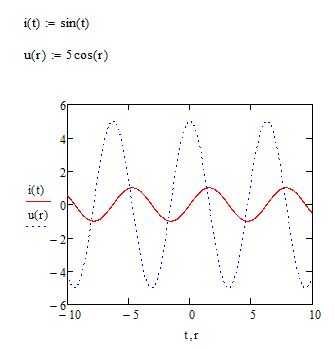
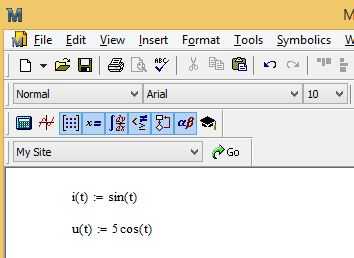
Mathcad предоставляет удобные инструменты для визуализации параметрических кривых, что особенно важно при работе с функциями, заданными через параметр. Чтобы построить график, необходимо определить параметрические уравнения для координат x(t) и y(t), где t – независимая переменная, задающая ход кривой.
В Mathcad параметр t удобно задавать как вектор с шагом, соответствующим желаемой точности графика. Оптимальный выбор шага зависит от гладкости кривой, обычно это значения в диапазоне от 0.01 до 0.1. Неправильный выбор шага может привести к искажениям или излишней детализации.
После определения функций и параметра необходимо использовать встроенную функцию построения графика, указав в качестве аргументов вычисленные векторы координат. Для наглядности рекомендуется задать подписи осям и диапазон отображения, что улучшит восприятие результатов и позволит точнее анализировать форму кривой.
Подготовка параметрических уравнений для построения
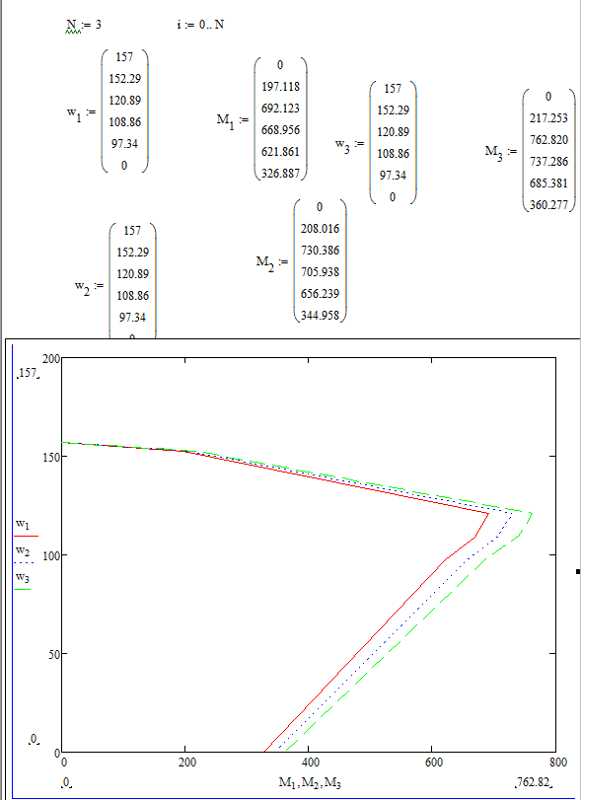
Перед построением параметрической кривой в Mathcad необходимо корректно задать функции координат в зависимости от параметра. Это позволит обеспечить точность и управляемость графика.
- Определите параметр \( t \) и его диапазон изменения. В Mathcad параметр задается как переменная с конкретным интервалом, например:
t := 0, 0.01..2π. Частота дискретизации влияет на гладкость графика. - Запишите уравнения для координат \( x(t) \) и \( y(t) \) в виде функций с четким использованием параметра. Например:
x(t) := cos(t),y(t) := sin(t). - Избегайте вложенных функций без необходимости, чтобы Mathcad корректно вычислял значения по всему диапазону параметра.
- Проверьте непрерывность и область определения функций, особенно если присутствуют выражения с делением или корнями, чтобы исключить ошибки вычислений.
- Используйте встроенные константы и функции Mathcad, чтобы избежать синтаксических ошибок и повысить производительность вычислений.
Тщательная подготовка параметрических уравнений гарантирует, что построенный график точно отобразит заданную кривую без искажений и с нужной детализацией.
Настройка диапазона параметра и шагов вычислений
Размер шага напрямую влияет на точность и плавность графика: слишком большой шаг приводит к угловатости кривой, слишком маленький – к избыточным вычислениям и замедлению работы. Для кривых с интенсивными изменениями рекомендуется шаг в пределах 0.001–0.005, для более гладких – 0.01–0.05.
Если требуется динамическая настройка, можно определить шаг через параметр, например dt := (t_end - t_start) / N, где N – количество вычислительных точек. Это позволяет легко увеличить точность без изменения всего диапазона.
При сложных кривых, имеющих локальные особенности, рационально разбивать диапазон параметра на сегменты с разными шагами и объединять результаты для повышения качества построения.
После задания диапазона параметра следует проверить, что все функции, задающие координаты, корректно принимают векторные значения параметра для векторных вычислений Mathcad. Это обеспечит автоматическое построение массива координат и последующую отрисовку графика.
Создание векторных выражений для координат X и Y
Для построения параметрической кривой в Mathcad требуется задать векторные выражения для координат X и Y, зависящие от параметра t. Начинайте с определения диапазона параметра, например, используя выражение t := 0, 0.01..2π, где 0.01 – шаг дискретизации, а 2π – верхняя граница.
Далее задайте функцию для X(t), используя векторные операции Mathcad. Например, X := cos(t) создаст вектор значений косинуса для каждого значения параметра t. Аналогично определите Y, например, Y := sin(t).
Важно, чтобы выражения X и Y были одинаковой длины, что гарантируется одинаковым диапазоном и шагом параметра t. Это позволяет Mathcad корректно построить график, интерпретируя пары (X[i], Y[i]) как точки кривой.
При необходимости используйте более сложные формулы, комбинируя функции и операции над векторами. Например, для эллипса: X := a * cos(t), Y := b * sin(t), где a и b – константы, определяющие размеры по осям.
Проверяйте результаты вычислений векторных выражений через отображение значений переменных, чтобы убедиться в правильности формул и параметров. Корректно заданные векторные выражения обеспечивают точное и плавное отображение параметрической кривой.
Построение графика с использованием встроенных функций Mathcad
Для построения графика параметрической кривой в Mathcad применяют функции построения графиков, такие как plot или встроенные графические объекты. Начинайте с определения параметрической функции как векторных выражений для координат, например, x(t) и y(t), где t – параметр.
Задайте область параметра t через диапазон с шагом, например, t := 0, 0.01..2π. В Mathcad диапазон автоматически создает вектор значений.
Для построения графика используйте встроенный инструмент «График XY». Вставьте график, дважды кликните на область графика и присвойте по оси X выражение x(t), по оси Y – y(t). Mathcad автоматически отобразит кривую по заданным координатам.
Оптимально задавать шаг параметра t достаточно мелким, чтобы кривая была гладкой, но не чрезмерно маленьким – чтобы избежать лишних вычислений и снижения производительности.
Для улучшения визуализации можно настроить свойства графика: толщину линии, цвет, тип маркеров через контекстное меню графика.
Встроенные функции Mathcad позволяют дополнительно добавлять несколько параметрических кривых на один график, создавая сложные композиции, используя множественные векторы координат.
Для функций, заданных аналитически, рекомендуется предварительно проверить корректность вычислений точек, отображая отдельные значения x(t) и y(t), что облегчает отладку графика.
Настройка внешнего вида графика: линии, точки и подписи
В Mathcad настройка графика параметрической кривой начинается с выбора типа линии. Для этого в меню графика активируют свойства линии и задают толщину в диапазоне от 0.5 до 3 пунктов, что позволяет подчеркнуть важные детали без перегруженности. Цвет линии рекомендуется выбирать из стандартной палитры, где контрастные оттенки улучшают читаемость при наложении нескольких кривых.
Точки на графике задаются параметром маркера. Оптимально использовать маркеры типа «круг» или «квадрат» с размером от 3 до 7 пикселей для визуального обозначения ключевых значений параметра. Цвет точек должен гармонировать с линией, но при этом выделяться, например, темнее или светлее базового цвета.
Подписи осей и самой кривой настраиваются через свойства текста. Рекомендуется применять шрифты с четкой засечкой, размером от 10 до 14 пунктов, чтобы обеспечить читаемость без искажения пропорций графика. Для подписи параметра или легенды следует избегать насыщенных цветов и использовать прозрачность 70–80%, что не отвлекает от основного изображения.
Кроме стандартных надписей, полезно добавлять метки на ключевых точках кривой через встроенный инструмент «Текст на графике». Для каждой метки задают положение с точной координатой и применяют одинаковый шрифт, обеспечивая единообразие и удобство восприятия.
При работе с несколькими кривыми настройка внешнего вида требует согласованности цветов и маркеров, чтобы пользователь безошибочно различал элементы. Mathcad позволяет сохранять шаблоны стилей, что ускоряет повторное построение графиков с одинаковыми параметрами отображения.
Проверка и отладка параметрической кривой на ошибки
Для корректного построения параметрической кривой в Mathcad необходимо последовательно проверить функцию параметров и диапазон изменения параметра. Начните с оценки выражений для x(t) и y(t) по отдельности, подставляя контрольные значения t. Это позволит выявить синтаксические ошибки и неверные формулы.
Убедитесь, что область определения параметра t задается корректно: шаг изменения должен быть достаточно мал, чтобы кривая была гладкой, но не настолько, чтобы замедлять вычисления. Оптимальный шаг обычно выбирается из интервала [0.01; 0.001].
Проверьте, что функции x(t) и y(t) возвращают числовые значения, а не векторы или неопределённые выражения. Для этого используйте встроенную функцию Mathcad isnumber() на нескольких точках параметра.
При появлении неожиданных разрывов или резких скачков кривой проверьте наличие особенностей в функциях – деление на ноль, корень из отрицательного числа или логарифм отрицательного аргумента. В таких случаях целесообразно ограничить область параметра или применить условные операторы для исключения проблемных значений.
Для упрощения отладки постройте отдельные графики x(t) и y(t), чтобы выявить неочевидные аномалии и лучше понять поведение параметров.
Если кривая не отображается или строится некорректно, проверьте правильность объявления векторов параметра t, особенно убедитесь, что параметры заданы как вектор, а не как скаляр.
Наконец, при комплексных выражениях полезно разбить формулы на части с присвоением промежуточных переменных. Это упрощает обнаружение логических ошибок и позволяет пошагово проверять корректность вычислений.
Вопрос-ответ:
Как задать параметрическую функцию для построения кривой в Mathcad?
В Mathcad параметрическую кривую можно задать через функции, определяющие координаты x(t) и y(t) в зависимости от параметра t. Для этого нужно создать два выражения: одно для x и другое для y, используя одинаковую переменную параметра. Например, x := t^2, y := sin(t). После этого для построения графика следует выделить область с этими функциями и вставить график с параметром t по оси X.
Какие шаги нужны для отображения графика параметрической кривой в Mathcad?
Сначала необходимо определить параметр, обычно обозначаемый как t, и задать его диапазон значений. Далее вводятся функции для координат x и y, зависящие от t. После этого создаётся график, выбирается тип графика «Параметрический» и указываются функции x(t) и y(t). Затем настраиваются оси и масштаб, чтобы кривые были хорошо видны. В итоге получается визуальное представление параметрической кривой.
Можно ли построить несколько параметрических кривых на одном графике в Mathcad? Если да, как это сделать?
Да, Mathcad позволяет строить несколько параметрических кривых на одном графике. Для этого создаются отдельные пары функций x(t) и y(t) для каждой кривой с разными параметрами или диапазонами t. После этого в одном графическом окне добавляются все функции, задавая их как отдельные кривые. Это удобно для сравнения различных параметрических зависимостей на одном рисунке.
Какие ошибки чаще всего возникают при построении параметрической кривой в Mathcad и как их избежать?
Одна из распространённых ошибок — неправильное задание диапазона параметра t, из-за чего график может быть неполным или искажённым. Ещё часто функции x(t) и y(t) задаются с ошибками в синтаксисе, что приводит к отсутствию графика. Чтобы избежать проблем, нужно внимательно проверять правильность формул и выбирать адекватный диапазон параметра. Также важно убедиться, что тип графика выбран корректно — именно параметрический.
Можно ли изменить стиль и цвет линии параметрической кривой в Mathcad, и как это сделать?
Да, в Mathcad доступна настройка внешнего вида графиков. Для изменения цвета и стиля линии нужно кликнуть по графику, открыть свойства графика, где можно выбрать цвет, толщину линии, тип линии (сплошная, пунктирная и др.). Эти параметры позволяют сделать график более наглядным и соответствующим требованиям презентации или отчёта.
Как в Mathcad задать параметрическую кривую для построения графика?
Для создания графика параметрической кривой в Mathcad необходимо сначала определить параметрическую функцию, задав координаты точек как функции от параметра, обычно обозначаемого как t. Например, если у вас есть уравнения x = f(t) и y = g(t), то нужно определить две функции в Mathcad: одну для x(t), другую для y(t). После этого выбирается диапазон изменения параметра t, и с помощью графического инструмента Mathcad строится двумерный график, где по оси X откладывается x(t), а по оси Y — y(t). Важно следить, чтобы значения t были заданы корректно и чтобы функции были определены для всего интервала.