Как построить кусочную функцию maple

Кусочные функции представляют собой важный инструмент в инженерных расчетах, численном моделировании и обучении методам анализа. В Maple построение таких функций реализуется с помощью оператора piecewise, который позволяет точно определить границы участков и задать индивидуальные выражения для каждого промежутка.

Формат записи кусочной функции в Maple следующий: piecewise(условие1, выражение1, условие2, выражение2, …, выражение_иначе). Каждое условие может включать логические операторы (and, or, not) и неравенства, например: x < -1 или -1 <= x and x < 2. Завершающее выражение применяется в случае, если ни одно из условий не выполняется.

Для визуализации кусочной функции используется команда plot. При передаче функции piecewise в plot(f, x = a..b), важно указывать границы отображения, так как Maple не определяет их автоматически по условиям функции. Ошибки на этом этапе чаще всего связаны с несогласованностью промежутков или отсутствием общего покрытия всей области определения.

Для повышения читаемости и отладки рекомендуется использовать оператор simplify после определения функции. Это позволяет устранить дублирование выражений и проверить корректность логики. Также стоит использовать assume при необходимости ограничить переменную в конкретной области значений, чтобы Maple корректно интерпретировал условия.

Создание базовой кусочной функции с помощью конструкции piecewise

В Maple для задания кусочной функции применяется встроенная конструкция piecewise, позволяющая явно определить значения функции на различных интервалах. Синтаксис следующего вида:

f := x -> piecewise(условие1, выражение1, условие2, выражение2, ..., выражение_иначе);

Каждая пара условие, выражение описывает участок области определения. Последнее выражение выполняется, если ни одно из условий не выполняется.

Переменная должна быть определена явно, например f := x -> ....
Условия задаются логическими выражениями: x < 0, 0 <= x and x < 2 и т.д.
Допустимы любые выражения в теле функции: числа, алгебраические выражения, другие функции.

Пример: определим функцию f(x), равную:

−1 при x < 0
x^2 при 0 <= x and x < 2
3 при x >= 2

f := x -> piecewise(x < 0, -1, x >= 0 and x < 2, x^2, 3);

Для проверки корректности используют команду plot:

plot(f(x), x = -2 .. 4);

Если требуется задать разрыв или определить поведение в конкретной точке, необходимо явно указать условие с равенством. Например, задать f(2) = 0:

f := x -> piecewise(x < 0, -1, x >= 0 and x < 2, x^2, x = 2, 0, 3);

Упорядоченность условий критична: Maple проверяет их последовательно. Самое общее условие (например, иначе) должно быть последним, иначе оно перекроет последующие участки.

Пошаговое определение условий для каждой части функции

При построении кусочной функции в Maple важно точно определить, какие условия должны быть выполнены для каждой части. Рассмотрим пошаговый процесс, который поможет правильно задать эти условия.

1. Разделите область определения на интервалы. Каждый интервал будет соответствовать одной части функции. Убедитесь, что интервалы не пересекаются и охватывают всю область определения функции.

2. Для каждого интервала определите, какое выражение функции будет использоваться. В Maple это можно сделать с помощью конструкции piecewise. Например, для интервала x < 2 используйте выражение f(x) := piecewise(x < 2, x^2). Важно, чтобы формулы в каждой части функции были корректными и не противоречили друг другу.

3. Установите условия перехода между частями функции. Если переход осуществляется на границе интервала, нужно учесть, будет ли функция непрерывной в этой точке. Для этого можно добавить дополнительные условия, например, f(2) = 4, если на границе функции должны быть соблюдены ограничения по значениям.

4. Проверяйте правильность определения условий с помощью построения графика. Maple позволяет визуализировать кусочные функции, что помогает убедиться, что условия на каждом интервале верны и функция корректно отображается.

5. В случае необходимости добавьте ограничения на переменные, чтобы исключить возможные погрешности. Например, если x должно быть положительным, добавьте условие x > 0 в соответствующую часть функции.

Графическое отображение кусочной функции в Maple

Для графического отображения кусочной функции в Maple используется команда piecewise, которая позволяет задавать разные выражения для разных интервалов. Однако для корректного построения графика кусочной функции важно правильно настроить параметры отображения и уточнить диапазоны значений.

Пример построения графика для кусочной функции может выглядеть следующим образом:

f := x -> piecewise(x < 0, x^2, x >= 0, x + 1);
plot(f(x), x = -5..5);

В этом примере функция имеет два выражения: для значений x, меньших нуля, используется квадратичная функция, а для значений x, больших или равных нулю, – линейная. Команда plot строит график на интервале от -5 до 5, что дает наглядное представление о поведении функции.

При построении графиков кусочных функций важно учитывать следующие моменты:

Переходы между кусками. Если функция меняет выражение на стыке интервалов, важно гарантировать, чтобы график корректно отображал эти переходы. Maple автоматически соединяет точки перехода, но можно уточнить этот момент с помощью дополнительных настроек.
Реальные и виртуальные разрывы. В случаях, когда функция имеет разрывы, стоит использовать параметр discontinuities, чтобы явно указать, где на графике должны быть отображены разрывы.
Мелкие детали графика. Можно настроить тип линии или добавить маркеры для отображения точек перехода через команду style.

Для более точного контроля за визуализацией кусочной функции можно использовать дополнительный параметр scaling, который позволяет масштабировать график, улучшая его читаемость, особенно на больших интервалах.

Пример с отображением разрывов:

f := x -> piecewise(x < 0, x^2, x = 0, undefined, x > 0, x + 1);
plot(f(x), x = -5..5, discont = true);

Этот код строит график функции с разрывом в точке x = 0. Указание discont = true заставляет Maple отображать этот разрыв на графике.

Графическое представление кусочной функции помогает наглядно увидеть ее поведение на разных интервалах, что особенно полезно при решении задач, связанных с анализом функциональных зависимостей.

Работа с кусочной функцией, заданной на неравномерных интервалах

В Maple создание и анализ кусочных функций на неравномерных интервалах требует особого подхода. Неравномерные интервалы часто используются для более точного аппроксимирования данных, когда стандартные равномерные шаги не дают нужной точности. Рассмотрим, как можно построить и работать с такими функциями в Maple.

Для начала определим основные составляющие: кусочная функция обычно задается набором значений, соответствующих различным промежуткам на оси абсцисс. В отличие от равномерных интервалов, длина промежутков на неравномерных интервалах может варьироваться, что позволяет учитывать особенности изменения функции на различных участках.

Одним из способов задания кусочной функции является использование массива значений и соответствующих интервалов. Для этого можно воспользоваться командой piecewise, которая позволяет задать значения функции на разных участках. Однако для работы с неравномерными интервалами необходимо уточнить, что интервалы не будут равномерными по длине. Пример такой функции:

f := piecewise(x < 1, x^2, 1 <= x < 3, 2*x, x >= 3, x^3);

Этот код задает кусочную функцию, которая на первом интервале (x < 1) равна x², на втором (1 <= x < 3) – 2x, и на третьем (x ≥ 3) – x³. Для работы с неравномерными интервалами можно просто задать различные промежутки по мере необходимости, не ограничиваясь равномерностью.

Чтобы работать с кусочной функцией, заданной на неравномерных интервалах, важно контролировать границы этих интервалов. Maple предоставляет средства для интегрирования таких функций, а также для нахождения производных на каждом участке. Например, если необходимо вычислить производную функции на одном из интервалов, можно использовать команду diff, указав нужный диапазон.

Если интервалы неравномерны и нужно более гибко настроить шаги между точками, можно использовать список интервалов и значений функции для интерполяции. Для этого в Maple можно воспользоваться функцией Interpolation, которая позволяет создавать более точные аппроксимации функции между заданными точками, принимая во внимание неравномерные интервалы.

Пример использования интерполяции для функции, заданной на неравномерных интервалах:

data := [[0, 0], [1, 1], [2, 3], [4, 5]];
interp := Interpolation(data);

Этот код создает интерполированную функцию, которая аппроксимирует данные на неравномерных интервалах, между точками. Это полезно, когда необходимо получить более точные значения функции для промежуточных значений x.

Кроме того, важно учитывать особенности вычисления интегралов и других операторов для таких функций. Для интегрирования кусочной функции на неравномерных интервалах Maple использует численные методы, которые позволяют точно учитывать различия в длине интервалов. Например, можно использовать функцию int с численными методами интеграции, если аналитическое решение невозможно.

В целом, работа с кусочными функциями на неравномерных интервалах в Maple требует внимательности при задании интервалов и применении соответствующих функций для анализа и вычислений. Мощные возможности Maple позволяют эффективно решать такие задачи, обеспечивая необходимую точность и гибкость при работе с функциями, заданными на неравномерных промежутках.

Использование переменных и параметров внутри piecewise-функций

В Maple использование переменных и параметров внутри функции piecewise позволяет создавать гибкие математические модели, которые можно адаптировать под различные условия. Правильное использование этих элементов повышает универсальность и эффективность кода.

При создании кусочных функций можно использовать как переменные, так и параметры. Различие между ними заключается в том, что переменные принимают конкретные значения в процессе вычислений, в то время как параметры остаются фиксированными при определении функции и могут изменяться при необходимости.

Использование переменных

Переменные внутри кусочных функций часто используются для задания различных условий, например, для определения диапазонов значений, при которых функция будет принимать разные выражения. В Maple переменные не ограничены типами данных и могут быть использованы для задания условий внутри функции.

Пример использования переменной x в piecewise-функции:


f := piecewise(x < 0, -x, x = 0, 0, x > 0, x^2);

В данном примере функция возвращает значения в зависимости от того, меньше ли x нуля, равно ли нулю или больше нуля. Важно, что переменные в условиях могут быть выражены через другие переменные или параметры.

Использование параметров

Параметры используются для задания фиксированных значений, которые могут изменяться при необходимости, но остаются одинаковыми для всех вычислений в рамках данной функции. Параметры помогают создать более универсальную функцию, которая легко подстраивается под разные задачи.

Пример использования параметра a в piecewise-функции:


a := 2;
f := piecewise(x < 0, a*x, x >= 0, x^2);

Здесь параметр a умножает значение переменной x на 2, если x меньше нуля, и оставляет выражение x^2 для значений x >= 0.

Совмещение переменных и параметров

Часто возникает необходимость совмещения переменных и параметров в одной кусочной функции. Это позволяет значительно расширить функциональность и разнообразить возможные варианты вычислений. Например, можно использовать параметры для задания различных характеристик функций, таких как коэффициенты, и переменные для выполнения вычислений.

Пример с параметром и переменной:


a := 3; b := 4;
f := piecewise(x < a, x^2 + b, x >= a, 2*x + b);

В данном примере параметр a используется для задания порога, при котором меняется выражение, а параметр b добавляется в оба участка функции. Использование переменных и параметров в таком сочетании делает код более компактным и легко изменяемым при необходимости.

Анализ разрывов и точек разветвления на графике

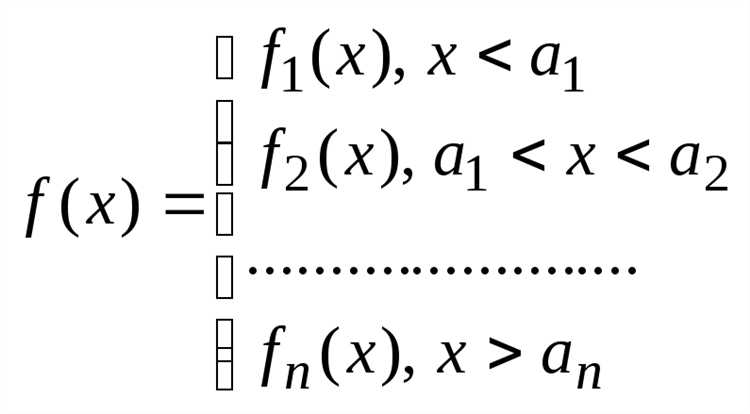
При построении кусочных функций в Maple необходимо учитывать наличие разрывов и точек разветвления. Эти особенности графика играют важную роль в анализе поведения функции и ее интерпретации в реальных задачах. Разрывы и точки разветвления могут существенно изменять характер графика и влиять на точность вычислений, поэтому важно точно выявить и правильно интерпретировать такие особенности.

Разрывы функций в контексте кусочных графиков могут быть как простыми, так и более сложными (например, скачки или разрывы второго рода). Maple предоставляет инструменты для анализа таких ситуаций, позволяя вычислить пределы функции с обеих сторон разрыва, а также определять тип разрыва: конечный, бесконечный или непределённый.

Точки разветвления возникают, когда функция изменяет свой характер в зависимости от направления. Это может быть связано с изменением структуры функции на разных участках, особенно если функция задана через несколько подфункций с различными условиями. Такие точки требуют особого внимания, так как они могут приводить к резким изменениям на графике.

Для выявления разрывов в Maple можно использовать функцию piecewise для построения кусочных функций, а также анализировать поведение функции с помощью операторов limit и diff для вычисления пределов и производных вблизи потенциальных разрывов.

В случае, если разрыв в функции сопровождается точкой разветвления, важно также проверять её производные и поведение функции на разных участках. Например, если функция изменяет свою область определения или есть пересечение ветвей, нужно убедиться, что они не влияют на общую непрерывность графика.

Для практического анализа можно использовать следующий алгоритм:

Построить график кусочной функции с использованием команды plot и проанализировать его визуально.
Вычислить пределы функции в точках предполагаемых разрывов с помощью команды limit.
Определить тип разрыва (если это необходимо) и проанализировать его влияние на график.
Проверить поведение функции в точках разветвления, учитывая все условия, которые могут изменить её форму.

Преобразование кусочной функции в аналитическую форму

Кусочная функция представляет собой набор взаимосвязанных функций, определённых на различных интервалах. Преобразование такой функции в аналитическую форму предполагает нахождение единого выражения, которое корректно аппроксимирует поведение функции на всём её области определения, объединяя все части в одно уравнение.

Для начала необходимо определить область определения кусочной функции и интервал, на котором происходит изменение её поведения. В Maple для работы с кусочными функциями используется команда piecewise, которая позволяет задать несколько частей функции на различных интервалах. Каждая часть может быть выражена через аналитическую формулу.

Для преобразования кусочной функции в аналитическую форму важно учитывать следующие шаги:

1. Анализ разрывов и непрерывности: Прежде чем объединить части функции, важно оценить, существуют ли разрывы или точки перехода между сегментами. Если функция непрерывна, можно попытаться найти универсальное аналитическое представление для всех её частей. В случае разрывов потребуется отдельно учитывать поведение функции в этих точках.

2. Выравнивание функций на стыках: Между различными частями кусочной функции должны быть выравнивающие выражения, которые обеспечат непрерывность функции или, в случае разрыва, будут описывать его форму. Это можно реализовать с помощью предельных переходов, использующих команду limit для анализа поведения функции в границах интервалов.

3. Использование условных выражений: В Maple можно использовать условные выражения, такие как if-else, для интеграции разных функций в одну. Это позволяет задать аналитическое выражение, которое будет правильно работать в зависимости от значений переменных на каждом интервале.

4. Определение переходных значений: Если части функции изменяются в определённых точках, необходимо вычислить значения функции в этих точках и использовать их для корректного соединения разных её сегментов. В Maple это может быть выполнено с помощью команд, таких как evalf, для численной оценки значений функции в переходных точках.

Для завершения процесса преобразования кусочной функции в аналитическую форму, требуется объединить все компоненты и убедиться, что полученная функция корректно описывает поведение исходной кусочной функции на всём её интервале.

Сравнение нескольких кусочных функций на одном графике

В Maple можно эффективно визуализировать несколько кусочных функций на одном графике, чтобы понять их поведение и выявить общие или различающиеся черты. Для этого необходимо использовать команду plot(piecewise(...)), которая позволяет строить графики функций, заданных различными правилами на разных интервалах.

При сравнении нескольких кусочных функций важно учитывать следующие моменты:

Каждая функция может быть задана различным количеством промежутков, что влияет на их вид. Например, одна функция может быть непрерывной на всем интервале, а другая – иметь разрывы в определённых точках.
Для точного наложения графиков на одном изображении важно правильно выбрать область определения для всех функций. Неправильно выбранные пределы оси X могут привести к неверной интерпретации данных.
При добавлении нескольких функций на один график следует контролировать цвета и стили линий, чтобы избежать путаницы и улучшить восприятие. В Maple это можно сделать через опцию style.

Пример кода для отображения двух кусочных функций:

f1 := piecewise(x < 0, x^2, x >= 0, 2-x);
f2 := piecewise(x < -1, -x, x >= -1 and x < 1, x^3, x >= 1, -x+2);
plot([f1, f2], x=-2..2, color=["red", "blue"], style=line);

В данном примере функция f1 имеет квадратичное поведение для отрицательных значений и линейное для положительных, в то время как функция f2 меняет свою форму на каждом промежутке: линейная часть для значений x < -1, кубическая для интервала -1 ≤ x < 1 и линейная с отрицательным угловым коэффициентом для значений x ≥ 1.

После построения графиков важно обратить внимание на:

Точки разрыва или соединения функций. В примере выше функция f1 имеет соединение в точке 0, а функция f2 – в точках -1 и 1.
Конкуренцию за пространство на графике. Если функций слишком много, график может стать перегруженным. В таком случае стоит использовать разные цвета, стили линий или уменьшить плотность точек на графике.
Оценку поведения функций на их промежутках, особенно в местах разрыва или изменений формы. Это можно сделать через дополнительное аннотирование графика для лучшего представления.

Для более точного анализа рекомендуется использовать различные масштабы для отображения функций, а также добавить сетку или оси для лучшего понимания пересечений функций.

Вопрос-ответ:

Какие ограничения могут возникнуть при построении кусочной функции в Maple?

При построении кусочных функций в Maple следует учитывать несколько аспектов. Во-первых, нужно правильно задать интервалы, чтобы не было перекрытия условий. Например, если вы зададите два одинаковых условия для разных интервалов, Maple не сможет правильно построить такую функцию. Во-вторых, если функции на разных интервалах содержат неограниченные выражения или функции, могут возникнуть проблемы с их вычислением или отображением на графике. Чтобы избежать таких проблем, стоит проверять корректность введенных функций и условий, особенно при использовании более сложных математических выражений.