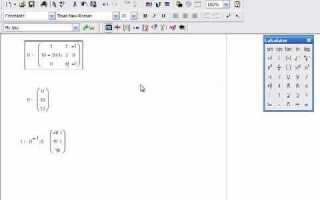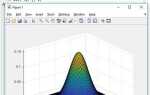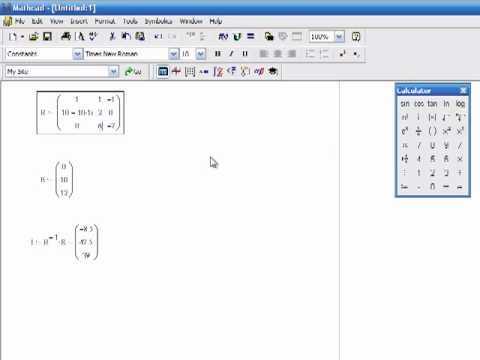
Для визуализации сложных функций двух переменных в Mathcad используется оператор plot3D. Он позволяет построить поверхность по заданному выражению z = f(x, y) с определёнными диапазонами переменных и шагом дискретизации. Построение требует чёткого задания сетки: векторов аргументов x и y, на основе которых формируется матрица значений z.
Типичный пример: определить векторы x := 0, 0.1 .. 10 и y := 0, 0.1 .. 10, после чего построить матрицу Z с помощью функции Z := xᵀ ⋅ y или другой зависимости. Важно помнить, что Mathcad воспринимает строки как векторы-столбцы, а столбцы – как векторы-строки, поэтому требуется транспонирование при необходимости. Размерность матрицы Z должна соответствовать длинам векторов x и y.
Окно построения графика позволяет задавать цветовые карты, прозрачность, точки сетки и направление освещения. При работе с математически сложными функциями (например, содержащими синусы, логарифмы или корни) нужно контролировать область определения, иначе график может не построиться. Mathcad не выдаёт ошибку напрямую, но пропускает точки с недопустимыми значениями, создавая разрывы на поверхности.
Для повышения наглядности рекомендуется добавлять подписи осей через свойства графика, а также проверять симметрию и корректность поверхности путём построения сечений. При необходимости уточнения структуры поверхности можно временно увеличить разрешение сетки, сократив шаги между значениями x и y.
Подготовка массивов данных для построения 3D-графика
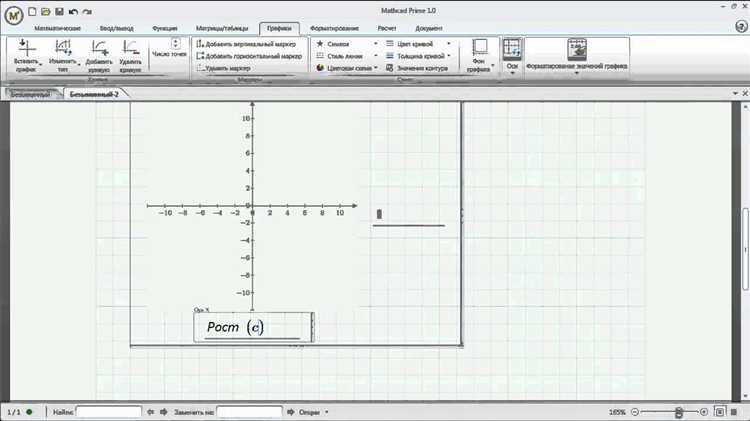
Для построения трёхмерной поверхности в Mathcad необходимо задать два вектора – оси X и Y, а также матрицу значений функции Z. Все три массива должны быть согласованы по размерности.
Ось X задаётся как вектор-строка: X := 0, 0.1 .. 10. Это создаёт равномерно распределённые точки с шагом 0.1. Аналогично формируется ось Y: Y := 0, 0.1 .. 5. Размерности X и Y определяют количество строк и столбцов итоговой матрицы Z.
Матрица Z создаётся с использованием встроенной функции stack или через вложенные циклы с применением for. Например, при определении функции f(x, y) := sin(x) * cos(y) матрица заполняется следующим образом:
Z := stack( f(X[i, all], Y[0]), f(X[i, all], Y[1]), ... ), где i пробегает индексы вектора Y. Для автоматизации используется вложенный цикл:
for i ∈ 0..last(Y)
for j ∈ 0..last(X)
Z[i, j := f(X[j], Y[i])
Если размеры векторов X и Y составляют N и M соответственно, итоговая матрица Z должна иметь размерность M×N. Несоответствие размеров приведёт к ошибке построения графика.
При работе с пользовательскими функциями рекомендуется проверять результат на наличие числовых значений (исключая NaN и комплексные числа), особенно при использовании корней, логарифмов и деления. Некорректные значения приводят к разрывам поверхности или её полной невозможности отображения.
Выбор функции и задания диапазонов переменных
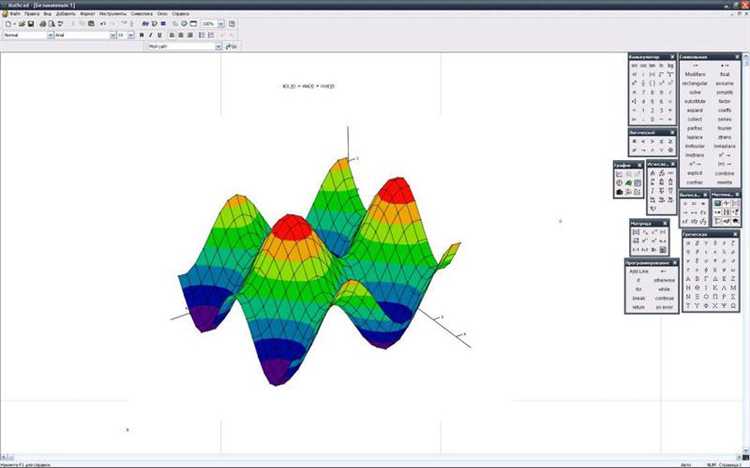
Перед построением трёхмерной поверхности в Mathcad требуется чётко определить аналитическое выражение функции двух переменных z = f(x, y). Примеры: z = sin(x)·cos(y), z = x² — y², z = exp(-x² — y²). Выражение должно быть непрерывным на заданной области, иначе график будет содержать разрывы или искажения.
Переменные x и y задаются с помощью векторов, создаваемых функцией диапазона. Например, x := -5, -4.9..5 задаёт значения от -5 до 5 с шагом 0.1. Шаг следует выбирать так, чтобы сохранить баланс между детализацией и производительностью. Для плавных поверхностей достаточно 100–200 точек по каждой переменной. Повышение плотности точек увеличивает нагрузку на систему и не всегда оправдано.
Если функция зависит от физических параметров, значения диапазонов необходимо согласовывать с реальными ограничениями. Например, при моделировании давления над поверхностью – учитывать допустимые значения координат.
При вычислении функции от векторов необходимо использовать векторизованные операции. Для этого в Mathcad используется символ векторизации – →. Пример: z ← f(x, y), где f – выражение с элемент-wise операциями.
Избегать слишком широких диапазонов: при значениях порядка ±100 и больше тригонометрические или экспоненциальные функции могут давать недостоверные значения из-за переполнения или потери точности. Проверка результата численно – обязательный этап перед визуализацией.
Использование команды plot для отображения поверхности
Для построения трёхмерной поверхности в Mathcad применяется команда plot с типом графика surface plot. Перед построением требуется задать два диапазона переменных – обычно x и y, а также функцию z = f(x, y).
Диапазоны определяются через выражение вида x := a, a+Δx .. b, где Δx – шаг. Аналогично задаётся y. После этого вычисляется матрица значений z, где каждый элемент соответствует результату функции при заданных x и y.
Для вызова графика нужно использовать вкладку «Графики» и выбрать «Поверхность». В окне графика указываются три аргумента: x, y и z. Mathcad автоматически создаёт сетку по указанным значениям и визуализирует поверхность.
Рекомендуется использовать шаги Δx и Δy не более 0.1 для детальной визуализации. При большем числе точек возможно замедление отрисовки. Поверхность корректно отображается только при наличии равномерной сетки и согласованных размеров векторов x и y и матрицы z.
Для изменения внешнего вида графика доступны параметры цвета, прозрачности, сетки и проекции. Эти настройки находятся в контекстном меню графика, которое вызывается двойным щелчком по области отображения.
Если функция содержит разрывы или сингулярности, рекомендуется ограничить диапазоны переменных, чтобы избежать некорректных значений в z. Mathcad не фильтрует ошибки вычислений автоматически, поэтому значения NaN в z могут привести к искажению графика.
Настройка параметров визуализации: сетка, цвет, угол обзора
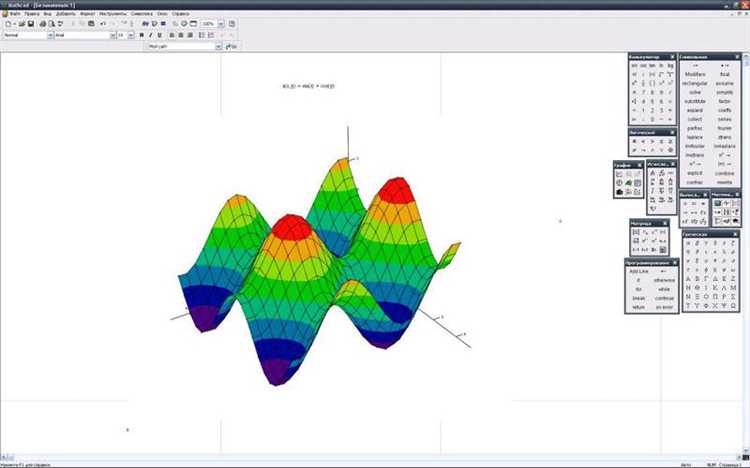
Для изменения плотности сетки трёхмерной поверхности в Mathcad используется параметр N – число точек по каждой оси. Значение по умолчанию – 25. Увеличение до 50 и выше повышает детализацию, но увеличивает нагрузку на систему. Оптимальное значение подбирается исходя из сложности функции и требуемой точности отображения.
Цвет поверхности регулируется через палитру, доступную при двойном щелчке по графику. Mathcad предлагает градиентную заливку, зависящую от значений функции. Для ручного выбора цветовой схемы используйте вкладку Color, где можно задать отдельные цвета для минимальных и максимальных значений, а также изменить цвет осей и фона.
Угол обзора задаётся параметрами Rotation и Elevation. Значения указываются в градусах: первый – поворот вокруг вертикальной оси, второй – наклон вверх или вниз. Например, Rotation = 45°, Elevation = 30° обеспечивает стандартную изометрическую проекцию. Для тонкой настройки лучше задать значения вручную, чем полагаться на мышь.
Для отключения отображения сетки снимите галочку Mesh Lines в настройках внешнего вида. Это может быть полезно при экспорте графика в презентации или отчёты. Если требуется только изменение цвета линий сетки, используйте вкладку Grid Color.
Преобразование выражений с параметрами в график поверхности
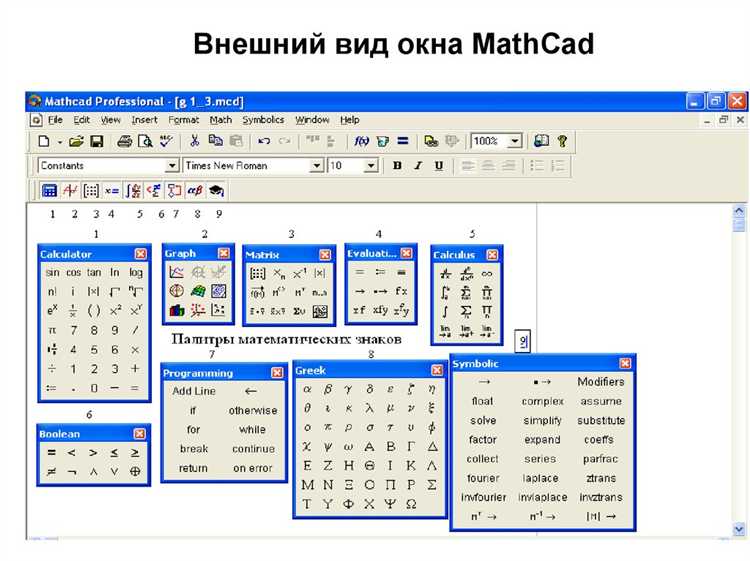
Для построения трёхмерной поверхности в Mathcad необходимо сначала определить выражение, содержащее два независимых параметра, обычно обозначаемых как x и y. Пример: z(x, y) := sin(x) * cos(y).
Перед построением следует задать диапазоны переменных. Используется оператор двоеточия:
x := 0, 0.1..10
y := 0, 0.1..10
Для вычисления значений функции создаётся двумерная матрица значений с помощью встроенной функции create meshgrid, либо вручную через вложенные циклы с использованием индексов и оператора stack.
Пример ручного создания матрицы:
for i ∈ 0..length(x)-1
for j ∈ 0..length(y)-1
Z[i,j := sin(x[i]) * cos(y[j])
После вычисления значений функции вызывается инструмент Insert → Graph → Surface Plot. В появившемся окне в соответствующие поля вводятся переменные:
| X | x |
| Y | y |
| Z | Z |
Для корректного отображения поверхности необходимо убедиться, что все три массива имеют одинаковые размеры. При несоответствии размерностей Mathcad выдаст ошибку визуализации.
Масштаб, цветовая схема и прозрачность поверхности настраиваются через двойной щелчок по графику. Отображение можно изменить вручную: скрыть сетку, отключить оси, изменить цветовую палитру через вкладку Format.
Для параметрических поверхностей, где координаты x и y сами задаются через параметры u и v, применяется аналогичный подход. Например:
u := 0, 0.1..2π
v := 0, 0.1..π
x(u,v) := sin(v) * cos(u)
y(u,v) := sin(v) * sin(u)
z(u,v) := cos(v)
В этом случае необходимо сгенерировать трёхмерные массивы X, Y, Z и передать их в график как аргументы.
Добавление ограничений и условий на отображаемую область
Для точного задания области построения трёхмерной поверхности в Mathcad необходимо применять ограничения к переменным и функциям. Это позволяет избежать избыточных или неуместных данных на графике и сосредоточиться на интересующем диапазоне.
- Ограничение параметров. В Mathcad область задания переменных ограничивается с помощью операторов диапазона, например,
x := 0, 0.1..5определяет значения x от 0 до 5 с шагом 0.1. - Использование условных операторов. В выражениях можно добавить условия, например,
z(x,y) := if (x^2 + y^2 <= 4) then f(x,y) else 0. Это задаёт поверхность только внутри круга радиуса 2, остальные точки принимают значение 0. - Фильтрация данных для графика. При построении графика функции 3D возможно использовать массивы значений с заранее отсечёнными точками, не подходящими по условию, что обеспечивает чистоту и читаемость визуализации.
Применение ограничений на отображаемую область реализуется так:
- Определить диапазоны переменных, соответствующие интересующему участку.
- Внедрить условные выражения непосредственно в формулы функции для исключения нежелательных значений.
- Использовать встроенные средства Mathcad для работы с массивами и фильтрации, чтобы исключить точки вне области.
Такой подход предотвращает появление артефактов и упрощает анализ модели, делая график более информативным и точным.
Экспорт трёхмерного графика из Mathcad в графический файл
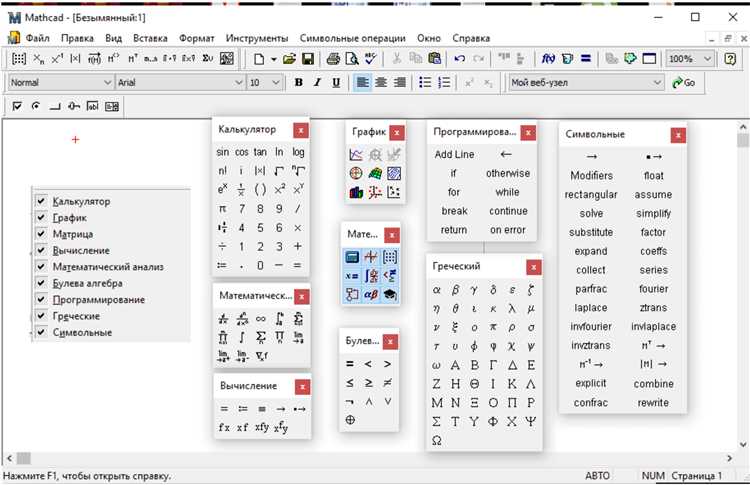
Для сохранения трёхмерной поверхности из Mathcad в графический файл необходимо использовать функцию экспорта графиков, встроенную в программу. После построения 3D-графика откройте контекстное меню графика правой кнопкой мыши и выберите пункт «Сохранить как изображение».
Mathcad поддерживает форматы PNG, JPEG и BMP. Для сохранения с максимальным качеством рекомендуется использовать PNG, так как этот формат сохраняет цвет и детали без потерь. Размер изображения можно задать вручную в пикселях, оптимально – не менее 1200×800 для последующей публикации или печати.
Если требуется векторное изображение, Mathcad напрямую не экспортирует в SVG или PDF. В этом случае используйте функции печати в PDF через системный драйвер печати, выбирая область с 3D-графиком. Такой способ сохраняет качество при масштабировании.
При экспорте стоит обратить внимание на угол обзора и масштаб графика, чтобы ключевые элементы поверхности были видны четко. Настройте эти параметры в свойствах графика до экспорта.
Для автоматизации процесса сохранения графиков применяйте скрипты на языке Mathcad Prime API (если доступен), которые позволяют программно задавать параметры и сохранять файлы без ручного вмешательства.
Вопрос-ответ:
Как задать трёхмерную поверхность в Mathcad?
В Mathcad трёхмерную поверхность можно создать, определив функцию двух переменных, например, z = f(x, y). Для этого сначала задаются диапазоны значений x и y с помощью операторов создания векторов или массивов. Затем создаётся матрица значений функции, вычисляемая на сетке, образованной этими диапазонами. После этого используется встроенная команда для построения графика поверхности, которая принимает матрицу значений и соответствующие оси x и y. Так визуализируется трёхмерная поверхность.
Какие ошибки чаще всего возникают при построении 3D поверхности в Mathcad и как их избежать?
Одна из распространённых проблем — неправильное определение области значений переменных. Если задать слишком большой или слишком мелкий шаг сетки, график может быть неинформативным или слишком «рваным». Также ошибки появляются при несовпадении размеров массивов x, y и матрицы z, что приводит к сбоям в построении. Чтобы этого избежать, нужно внимательно проверять размеры данных и использовать команды Mathcad для проверки диапазонов. Ещё важно убедиться, что функция корректно задана для всех точек сетки, чтобы не возникало деления на ноль или вычислений вне области определения.
Можно ли в Mathcad настроить цветовую заливку трёхмерной поверхности и как это сделать?
Да, Mathcad позволяет управлять цветом поверхности. В последних версиях программы можно выбрать разные цветовые схемы или задать собственные параметры. Обычно настройка цвета происходит через свойства графика, где можно указать цветовую палитру, степень прозрачности и интенсивность окрашивания. Это помогает выделить особенности поверхности, например, зоны с наибольшими или наименьшими значениями. Для этого нужно открыть меню параметров графика и изменить соответствующие настройки.
Как построить трёхмерную поверхность, если функция зависит от параметра?
Если функция содержит параметр, например z = f(x, y, a), то сначала нужно задать фиксированное значение этого параметра или создать цикл по разным значениям параметра. В Mathcad можно вычислить поверхность при конкретных параметрах, подставляя их в выражение функции. Для просмотра изменений можно строить несколько поверхностей на одном графике, используя разные цвета для каждого значения параметра. Это помогает увидеть, как параметр влияет на форму и поведение поверхности.