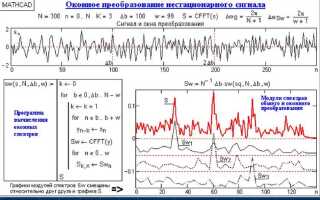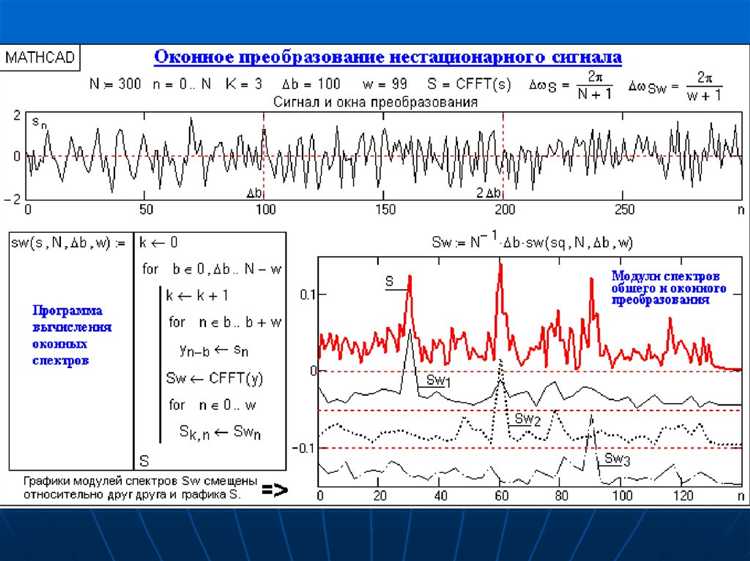
Для анализа сигнала в Mathcad ключевым этапом является построение его спектра с помощью быстрого преобразования Фурье (БПФ). Важно правильно подготовить исходные данные: временной ряд должен быть равномерно дискретизирован с постоянным шагом, а количество точек – степенью двойки для оптимизации вычислений.
Начинайте с импорта или задания массива значений сигнала, проверяя длину и однородность дискретизации. Затем задайте временной интервал и вычислите частоту дискретизации Fs. Для корректного построения спектра необходимо нормировать амплитуды преобразованных данных, учитывая длину выборки.
В Mathcad используйте встроенную функцию fft(), применяя ее к сигналу, и извлекайте амплитудный спектр как модуль комплексных значений результата. Для визуализации спектра настройте ось частот от 0 до Fs/2, так как спектр симметричен относительно половины частоты дискретизации.
Дальнейшие шаги включают интерпретацию пиков спектра для выявления основных гармоник и оценку ширины спектральной полосы, что позволяет выделять ключевые характеристики сигнала без излишних вычислительных затрат.
Подготовка данных сигнала для анализа в Mathcad
Перед построением спектра сигнала в Mathcad необходимо привести исходные данные к корректному виду. Во-первых, временная шкала должна быть равномерно дискретизирована с постоянным шагом Δt, иначе результат преобразования Фурье будет искажен. Для этого важно проверить и при необходимости пересчитать временные отметки, чтобы интервалы между точками были одинаковы.
Во-вторых, амплитудные значения сигнала должны быть числовыми и иметь однородный тип данных (обычно вещественный). Если исходный сигнал содержит шумы, рекомендуется применить предварительное фильтрование – например, скользящее среднее или фильтр низких частот, чтобы снизить влияние артефактов на спектр.
Также необходимо определиться с длительностью наблюдаемого сигнала. Для получения более точного спектра стоит выбрать длину выборки, равную степени двойки (например, 256, 512, 1024), что оптимизирует вычисления быстрого преобразования Фурье в Mathcad.
Для анализа амплитуды спектра важно нормализовать данные, если сигнал поступает из разных источников или измерен с разными усилениями. Нормализация сводится к делению всех значений на максимальное абсолютное значение сигнала, что упрощает последующую интерпретацию.
Наконец, в Mathcad следует задать векторы времени и амплитуды как столбцовые или строковые массивы, избегая смешивания форматов, что предотвратит ошибки при построении графиков и вычислении спектра. Четкое соответствие размерностей и форматов данных обеспечивает корректность и reproducibility анализа.
Настройка параметров дискретизации и временного интервала
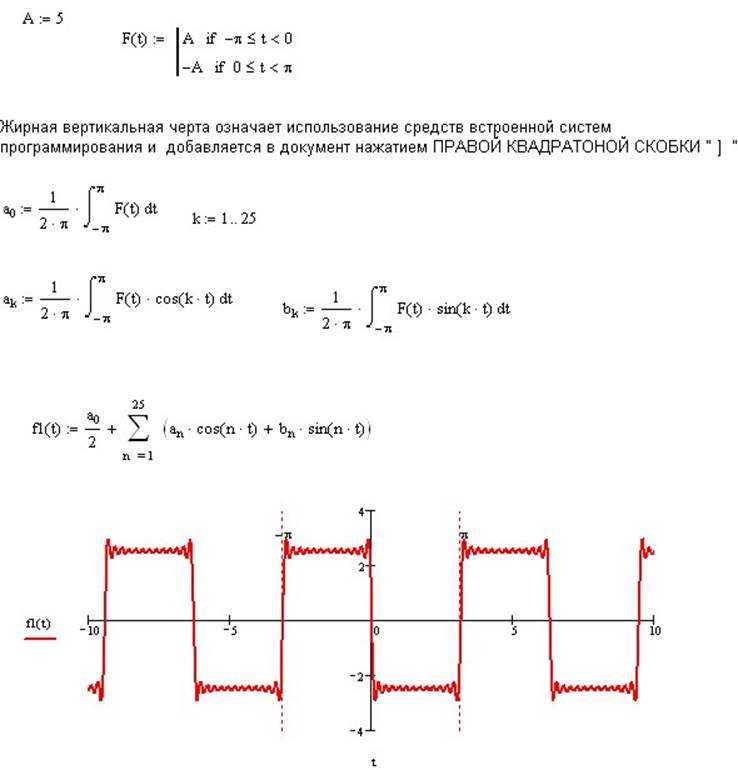
- Определение частоты дискретизации (Fs)
- Fs должна быть не меньше удвоенной максимальной частоты сигнала (Fs ≥ 2·Fmax) согласно теореме Найквиста.
- Для повышения точности спектра рекомендуется выбирать Fs с запасом 20-30% от минимального значения.
- В Mathcad задайте Fs как переменную и используйте ее при генерации временного вектора: t := 0, 1/Fs .. T.
- Выбор временного интервала (T)
- T влияет на разрешение спектра: Δf = 1/T. Чем больше T, тем выше разрешение.
- Оптимально выбирать T так, чтобы покрыть несколько периодов самой низкой частоты сигнала.
- Увеличение T требует большего объема данных и увеличивает время расчета.
- В Mathcad задайте T явно и создайте временной вектор с шагом 1/Fs.
- Практические рекомендации
- Начинайте с Fs в 5-10 раз выше основной частоты для качественной дискретизации.
- Установите T минимум в 5 периодов самой низкой частоты для четкого выделения спектральных линий.
- Проверяйте корректность временного вектора в Mathcad: длина массива = Fs × T.
- При необходимости применяйте оконные функции для снижения спектральных утечек.
Реализация функции преобразования Фурье в Mathcad
Для построения спектра сигнала в Mathcad используется дискретное преобразование Фурье (ДПФ), реализуемое через встроенную функцию fft(). Входными данными служит вектор значений сигнала, равномерно отсчитанного по времени.
Перед вызовом fft() необходимо определить временную сетку с постоянным шагом Δt, чтобы корректно интерпретировать частотную ось. Частотный вектор формируется как f = k/(N*Δt), где k – индекс отсчёта, N – длина сигнала.
Для получения амплитудного спектра после вычисления комплексного результата F = fft(x) используют модуль: A = abs(F)/N. Деление на N нормализует амплитуду, отражая реальные значения компоненты.
Для анализа действительной части сигнала достаточно рассмотреть первые N/2 значений спектра, так как ДПФ симметрично отображает отрицательные частоты.
Если сигнал не кратен степени двойки по длине, рекомендуется дополнить его нулями до ближайшей степени двойки для ускорения вычислений. Это реализуется через функцию augment(x, length).
Построение графика спектра выполняется с использованием частотного вектора и амплитудного спектра: plot(f[0..N/2-1], A[0..N/2-1]). При необходимости отображают спектр в децибелах, вычисляя 20*log10(A).
Пример полного цикла вычислений:
Δt := 0.001
N := length(x)
F := fft(x)
A := abs(F)/N
f := (0..N-1)/(N*Δt)
plot(f[0..N/2-1], A[0..N/2-1])
Таким образом, для корректной реализации преобразования Фурье в Mathcad важно правильно задать временной шаг, обеспечить нормализацию амплитуд и использовать только первую половину спектра для визуализации.
Построение амплитудного спектра сигнала
Для построения амплитудного спектра в Mathcad необходимо последовательно выполнить несколько точных шагов. Сначала задайте дискретный временной ряд сигнала, используя вектор с равномерным шагом, например, t := 0, Δt .. T. Частота дискретизации определяется как обратная величина шага: Fs := 1/Δt. Убедитесь, что длина временного вектора – степень двойки для оптимальной работы FFT.
Далее примените функцию быстрого преобразования Фурье: Y := fft(signal). Полученный комплексный вектор содержит амплитуды и фазы гармоник. Амплитудный спектр вычисляется как модуль комплексных чисел: A := abs(Y)/N, где N – длина сигнала.
Чтобы получить корректные амплитуды, необходимо умножить значения, кроме нулевой и центральной частоты, на 2, поскольку FFT возвращает значения для положительных и отрицательных частот. Диапазон частот формируется как f := Fs * (0 .. N/2) / N. Для построения графика используйте только половину спектра, соответствующую положительным частотам.
Затем вызовите функцию графика: plot(f, A[0 .. N/2]). В Mathcad рекомендуется задать метки осей и заголовок для наглядности. Важно проверять, что сигнал не содержит смещения по среднему, иначе спектр будет искажен компонентой постоянной составляющей.
Для точного анализа рекомендуется предварительно применять окно (например, Ханна или Хэмминга) к исходному сигналу, чтобы уменьшить спектральные утечки. Окно умножается покомпонентно на исходный ряд до FFT. Это значительно улучшает разрешение спектра, особенно для коротких сигналов.
Отображение фазового спектра в Mathcad
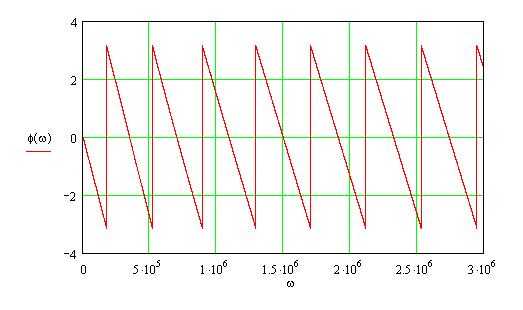
Для визуализации фазового спектра в Mathcad необходимо выполнить вычисление аргумента комплексных значений спектра. Если F(ω) – комплексный спектр сигнала, фазовый спектр определяется как φ(ω) = arg(F(ω)). В Mathcad функция arg(z) возвращает фазу комплексного числа z в радианах.
Пошаговый алгоритм отображения фазового спектра:
1. Вычислите комплексный спектр сигнала, используя встроенную функцию Дискретного Преобразования Фурье, например, fft(x), где x – исходный сигнал.
2. Создайте вектор частот, соответствующий дискретным точкам спектра. Для нормализованного спектра частоты задаются как f = (0..N-1) * (Fs/N), где N – количество точек, Fs – частота дискретизации.
3. Для каждого элемента спектра вычислите фазу с помощью функции arg(). В Mathcad это делается простым применением phase := arg(F), где F – вектор комплексных значений спектра.
4. При необходимости устраните скачки фазового спектра с помощью процедуры развёртки фазы (unwrap), которую можно реализовать через пошаговое сравнение соседних фаз и добавление/вычитание 2π при скачках выше порогового значения.
Особое внимание уделяйте индексации и согласованию размеров векторов частот и фаз. Неправильное построение оси частот или несоответствие размерности векторов приводит к искажённым графикам.
Использование оконных функций для улучшения спектра
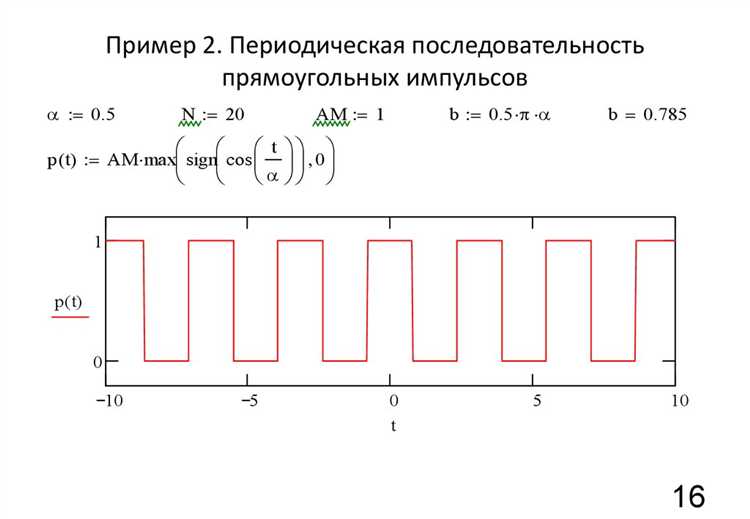
Наиболее распространённые окна – прямоугольное, Ханна, Хэмминга и Блэкмана. Прямоугольное окно – это отсутствие окна, дающее максимум разрешения, но с сильной утечкой. Окна Ханна и Хэмминга уменьшают боковые лепестки спектра примерно до −40…−45 дБ, при этом ширина главного лепестка увеличивается, что снижает частотное разрешение.
Для вычисления окна в Mathcad используется встроенный вектор с длиной N, к которому применяется формула окна. Например, окно Хэмминга задаётся формулой:
w(n) = 0.54 − 0.46·cos(2πn/(N−1)), n = 0, 1, …, N−1
Встроенные функции Mathcad позволяют быстро формировать окно и перемножать его с исходным сигналом, что снижает выбросы вне основной полосы частот.
Выбор окна зависит от задачи: если приоритет – минимизация боковых лепестков и подавление шума, предпочтительно использовать Блэкмана с уровнем боковых лепестков около −58 дБ. Если важна максимальная частотная разрешающая способность, подойдёт окно Ханна с компромиссом между разрешением и подавлением утечки.
Рекомендуется выполнять сравнительный анализ спектров с разными окнами на одном и том же сигнале для выбора оптимального варианта. Для визуализации результатов в Mathcad применяют графики амплитудного спектра, позволяющие оценить форму и уровень боковых лепестков.
Итог: оконные функции в Mathcad критичны для точности спектрального анализа, снижая артефакты и улучшая выделение частотных компонент, что повышает качество интерпретации данных.
Сравнение спектров различных сигналов в Mathcad
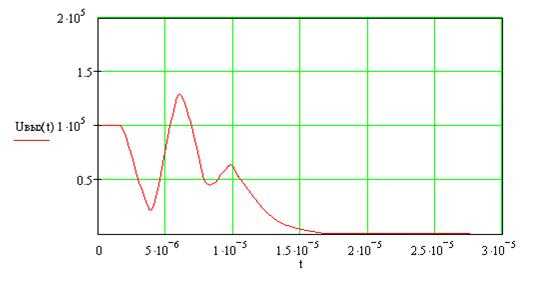
Для объективного сравнения спектров в Mathcad важно использовать единые параметры дискретизации и длину окна анализа. Различия в спектрах становятся отчетливыми при последовательном построении и наложении графиков.
- Определите временные ряды сигналов с одинаковой частотой дискретизации. Это позволит избежать искажений в спектральном анализе.
- Проведите преобразование Фурье каждого сигнала с использованием функции FFT Mathcad, контролируя количество точек преобразования (обычно степень двойки для оптимизации).
- Нормируйте амплитуды спектров для корректного сравнения, деля спектр на максимальное значение амплитуды.
- Используйте общий частотный вектор для всех сигналов, чтобы обеспечить точное совпадение оси X на графиках.
Пример практического сравнения:
- Синусоидальный сигнал с одной частотой демонстрирует узкий пик в спектре.
- Пилообразный сигнал показывает спектр с гармониками на кратных основной частоте, амплитуда которых уменьшается пропорционально обратной частоте.
- Белый шум характеризуется равномерным распределением амплитуд по всему частотному диапазону.
Для визуального сравнения наложите спектры на один график, используя разные цвета и легенду. В Mathcad это реализуется через добавление нескольких функций plot в одном графическом окне.
При анализе учитывайте влияние окна скважности и длины выборки на разрешение и сглаживание спектра. Для сигналов с близкими частотными компонентами применяйте окно Хэмминга или Ханна.
Таким образом, последовательное выполнение перечисленных шагов в Mathcad позволит выявить характерные особенности и различия спектров различных сигналов с высокой точностью и наглядностью.
Экспорт и сохранение результатов спектрального анализа
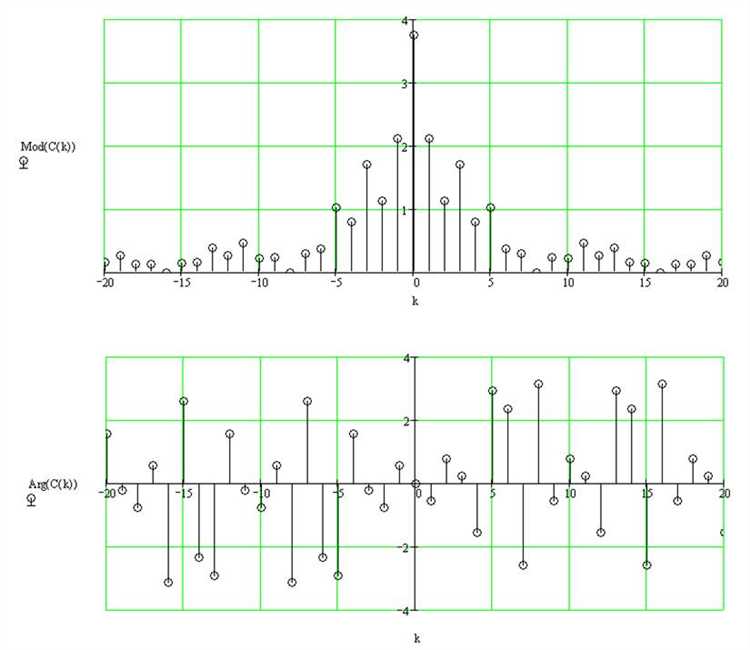
Перед сохранением рекомендуется уточнить масштаб осей и количество точек дискретизации, чтобы экспортированные данные соответствовали необходимой точности. Для получения файла с максимальным разрешением выставьте в настройках плотность точек спектра не менее 1000, что позволяет избежать потерь информации при дальнейшем анализе.
Для сохранения графического результата спектра используйте Export as Image с выбором форматов PNG или SVG. PNG подходит для быстрого просмотра и публикаций, SVG – для векторного редактирования и масштабирования без потери качества. При сохранении изображения убедитесь, что параметры графика установлены корректно: оси, подписи и масштаб должны быть четко видны.
Автоматизация экспорта возможна с помощью скриптов Mathcad, которые позволяют сохранять результаты спектрального анализа в заданной директории с уникальными именами файлов, включающими временные метки. Это особенно полезно при серийном анализе нескольких сигналов.
Для повторного использования сохранённых данных загружайте CSV-файлы с помощью функции Import, обеспечивая точное восстановление спектра для дальнейшего сравнения или усовершенствования моделей.
Вопрос-ответ:
Как в Mathcad задать исходный сигнал для дальнейшего построения его спектра?
Для начала необходимо определить функцию или набор значений, которые описывают сигнал во временной области. В Mathcad это можно сделать с помощью задания выражения функции или массива данных, соответствующих значению сигнала в дискретные моменты времени. Важно правильно выбрать временной шаг и длительность сигнала, так как они влияют на качество и точность спектрального анализа.
Какие шаги нужно выполнить для вычисления спектра сигнала с помощью преобразования Фурье в Mathcad?
Первым шагом создается временной массив и определяется сигнал. Затем применяется функция быстрого преобразования Фурье (FFT), доступная в Mathcad, к этому сигналу. После получения комплексных значений спектра следует вычислить амплитуду каждой гармоники через модуль комплексного числа. Наконец, формируется частотный массив, который соответствует элементам спектра, и строится график амплитуды спектра по частоте.
Как правильно настроить параметры FFT, чтобы избежать ошибок в спектре сигнала?
Важно следить за выбором количества точек дискретизации — их должно быть степенью двойки для корректной работы FFT. Также временной интервал между отсчетами должен быть постоянным. При этом длина сигнала и частота дискретизации напрямую влияют на разрешение и диапазон спектра. Для уменьшения спектральных утечек можно применить оконные функции, которые снижают влияние резких обрезок сигнала.
Какие особенности отображения спектра сигнала стоит учитывать при построении графиков в Mathcad?
При построении спектра обычно отображают амплитуду спектра по частоте, причем частоты должны быть представлены в правильном диапазоне от нуля до половины частоты дискретизации. Часто полезно использовать логарифмическую шкалу для амплитуды, чтобы лучше видеть слабые гармоники. Также нужно учитывать нормировку амплитуды, так как значения из FFT могут требовать масштабирования для корректного представления.
Как можно проверить корректность построенного спектра сигнала в Mathcad?
Один из способов — сравнить спектр с известной теоретической формой или с результатами, полученными другим методом. Например, для гармонического сигнала ожидается одна яркая линия на частоте сигнала. Можно проверить симметрию спектра для реальных сигналов и отсутствие неожиданных пиков. Также полезно менять параметры сигнала и наблюдать изменения в спектре, чтобы убедиться, что результаты адекватны.
Как в Mathcad можно получить спектр сигнала с помощью преобразования Фурье?
Для построения спектра сигнала в Mathcad необходимо сначала определить временной ряд значений сигнала, а затем применить к нему функцию дискретного преобразования Фурье (DFT). В Mathcad для этого используется встроенная функция FFT, которая принимает на вход массив значений сигнала и возвращает массив комплексных чисел, представляющих амплитуду и фазу частотных компонентов. После выполнения FFT следует вычислить модуль комплексных чисел, чтобы получить амплитудный спектр, и отобразить полученные значения на графике с осью частот. Важно правильно задать временной интервал и количество точек для корректного масштабирования частотной оси.