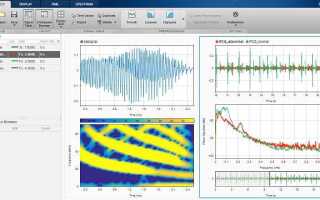Как построить спектр сигнала в matlab

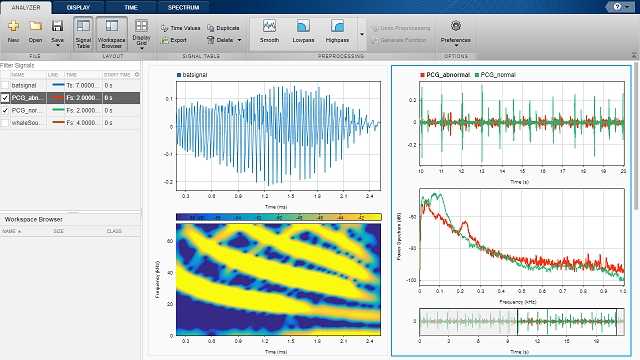
Анализ спектра сигнала – ключевая задача цифровой обработки, позволяющая выявить частотные компоненты, шумы и искажения. В MATLAB для спектрального анализа применяются функции fft, abs, linspace, а также инструменты визуализации – plot и stem. Правильная реализация спектра начинается с подготовки временного сигнала, выбора частоты дискретизации и построения частотной оси.

При использовании Fast Fourier Transform важно учитывать, что результат fft – это комплексный массив. Для получения амплитудного спектра применяется модуль: abs(Y), где Y = fft(x). Чтобы избежать симметрии, характерной для спектра действительного сигнала, отображается только первая половина отсчетов: Y(1:N/2), где N – длина сигнала. Частотная ось строится с учетом частоты дискретизации Fs: f = Fs*(0:(N/2)-1)/N.

Для корректной интерпретации спектра критично нормировать амплитуду. Если длина сигнала N, результат abs(fft(x))/N даст масштабированный спектр. Удвоение амплитуды (кроме DC и Nyquist-компонент) необходимо при использовании одностороннего спектра: 2*abs(Y(1:N/2))/N. Это гарантирует сохранение энергетического баланса при переходе к одностороннему представлению.

В MATLAB также доступны более точные методы, такие как pwelch и periodogram, реализующие оконный спектральный анализ. Они уменьшают утечки за счет оконных функций (Hamming, Hann, Blackman) и подходят для анализа реальных сигналов с ограниченной длительностью. Рекомендуется использовать pwelch при наличии шума или при анализе нестабильных сигналов.

Создание дискретного сигнала с заданными параметрами

Для генерации дискретного сигнала в MATLAB необходимо задать частоту дискретизации Fs, длительность сигнала T, частоту сигнала f и амплитуду A. Эти параметры определяют временную и спектральную структуру сигнала.

Пример: создадим синусоидальный сигнал с частотой 100 Гц, амплитудой 1, длительностью 0.1 секунды и частотой дискретизации 1000 Гц:

Fs = 1000;      % частота дискретизации, Гц
T = 0.1;        % длительность сигнала, сек
f = 100;        % частота сигнала, Гц
A = 1;          % амплитуда сигнала
t = 0:1/Fs:T-1/Fs;   % временной вектор
x = A * sin(2*pi*f*t); % сигнал

Длина вектора t должна соответствовать количеству отсчётов: N = Fs * T. Это необходимо для корректного анализа спектра. Если Fs меньше, чем удвоенная частота сигнала, возникает эффект наложения спектров (алиасинг), который искажает результат преобразования Фурье.

Для формирования сигнала с несколькими гармониками просто суммируйте синусоиды с разными частотами:

f1 = 100;
f2 = 250;
x = sin(2*pi*f1*t) + 0.5*sin(2*pi*f2*t);

При необходимости моделирования шума используйте встроенную функцию:

x = x + 0.1*randn(size(x)); % добавление белого гауссовского шума

Соблюдайте соотношение частот и временного разрешения: минимальное значение Fs должно быть как минимум в два раза больше максимальной частоты сигнала (критерий Найквиста), иначе анализ спектра будет некорректным.

Применение функции fft для получения спектра

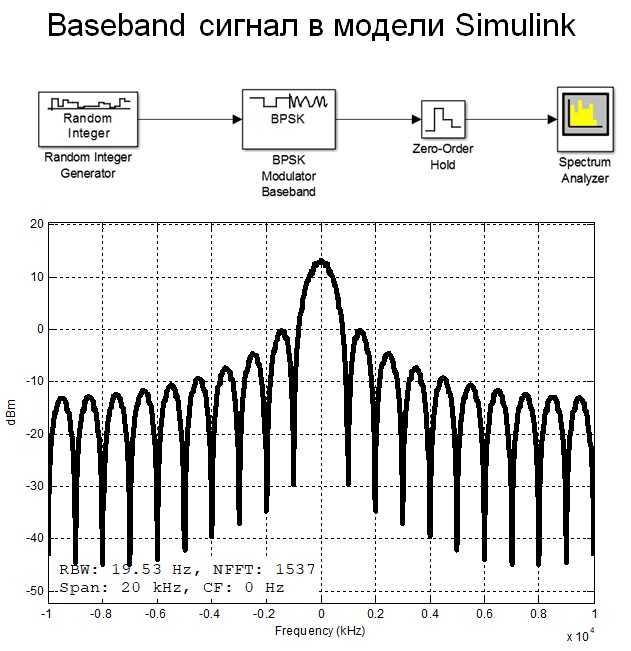
Функция fft в MATLAB вычисляет дискретное преобразование Фурье (DFT) сигнала, позволяя анализировать его частотное содержание. Для корректного спектрального анализа необходимо учитывать длину сигнала, окно аппроксимации и нормировку.

Прямое применение Y = fft(x) возвращает комплексный спектр. Для получения амплитудного спектра используют abs(Y), а фазового – angle(Y). Частотная шкала определяется выражением f = (0:N-1)*(Fs/N), где N – длина сигнала, Fs – частота дискретизации.

Для симметричного отображения спектра используют fftshift. Например: Y_shifted = fftshift(fft(x)). Частотная ось в этом случае задаётся как f = (-N/2:N/2-1)*(Fs/N).

Чтобы избежать искажений, перед применением fft рекомендуется применять окно (например, Хэмминга): x_win = x .* hamming(length(x)). Это снижает побочные лепестки и улучшает разрешение по частоте.

Нормировка спектра необходима для получения реальных амплитуд. Пример: Y_mag = abs(Y)/N. При использовании оконной функции следует дополнительно корректировать масштаб на её среднее значение.

Если длина сигнала не кратна степени двойки, предпочтительно применять fft(x, 2^nextpow2(length(x))) – это увеличит скорость вычислений за счёт оптимизации алгоритма БПФ.

Для анализа реального сигнала достаточно использовать только первую половину спектра: Y_half = Y(1:N/2+1), f_half = f(1:N/2+1). Это позволяет сократить объём данных без потери информации.

Нормализация и масштабирование амплитудного спектра

После применения БПФ к сигналу, амплитудный спектр требует корректной нормализации и масштабирования для получения достоверных характеристик частотного состава. В MATLAB нормализация производится делением на длину сигнала N, а масштабирование зависит от типа сигнала (односторонний или двусторонний спектр).

Для получения амплитуд в физических единицах необходимо нормализовать спектр: Y = abs(fft(x))/N, где x – входной сигнал, N – его длина.
При отображении одностороннего спектра (только положительные частоты) амплитуды, кроме первой и последней (нулевой и на частоте Найквиста), нужно удвоить: Y(2:end-1) = 2*Y(2:end-1).
Используйте linspace(0, Fs/2, N/2+1) для построения оси частот, где Fs – частота дискретизации.

При логарифмическом представлении спектра (например, в децибелах) применяется выражение:

20*log10(Y) – для амплитудного спектра;
10*log10(Y.^2) – для спектральной плотности мощности.

Нарушение масштабирования приводит к ложной интерпретации энергии сигнала и неверной идентификации гармоник. При работе с окнами (например, hamming, hann) учитывайте энергетическую поправку, деля результат на сумму коэффициентов окна: Y = abs(fft(x.*w))/sum(w).

Отображение частотной оси в герцах

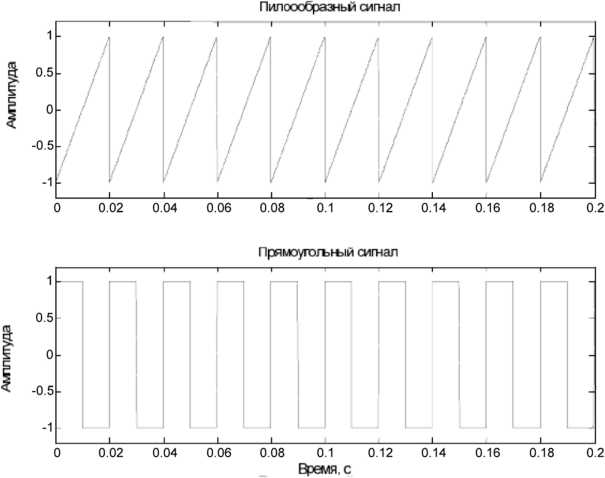
По умолчанию функция fft в MATLAB возвращает амплитудный спектр с индексами, соответствующими отсчетам частотного диапазона. Чтобы отобразить частотную ось в герцах, необходимо выполнить масштабирование с учетом частоты дискретизации сигнала.

Если длина сигнала равна N, а частота дискретизации – Fs, то вектор частот для прямого БПФ строится следующим образом:

f = (0:N-1)*(Fs/N);

Для симметричного отображения спектра с центром в нуле, особенно после применения fftshift, используют:

f = (-N/2:N/2-1)*(Fs/N);

plot(f, abs(fftshift(Y)))

Где Y – результат БПФ. Это позволяет интерпретировать спектр в физически значимых единицах – герцах, а не в индексах массива.

При анализе реальных сигналов важно ограничить частотную ось половиной частоты дискретизации – от 0 до Fs/2, что соответствует одностороннему спектру. Для этого используют только первые N/2 точек:

f = (0:N/2-1)*(Fs/N);

plot(f, abs(Y(1:N/2)))

Неправильное отображение частотной оси приводит к искаженной интерпретации спектральных составляющих. Использование приведенных формул гарантирует соответствие оси частот реальному масштабу сигнала.

Построение одностороннего и двустороннего спектра

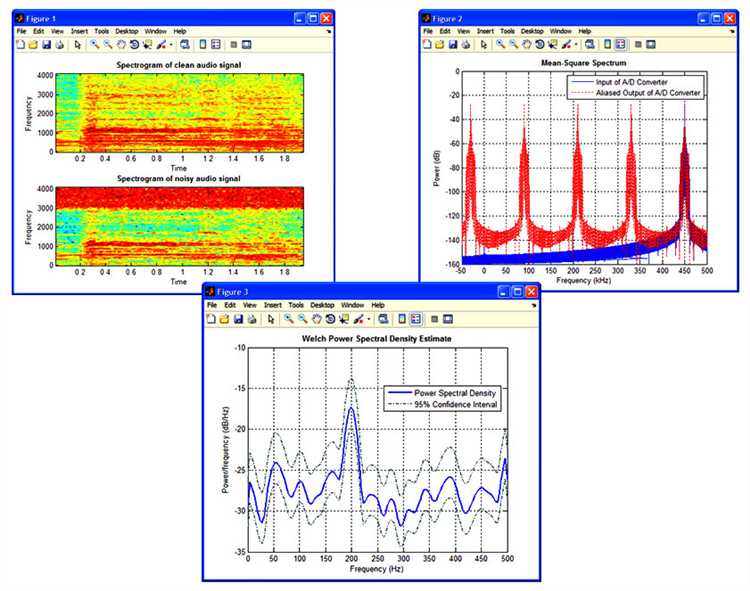
Двусторонний спектр рассчитывается напрямую из Y = fft(x), где x – временной сигнал. Частотная ось строится как f = (0:N-1)*(Fs/N) при условии, что N – длина сигнала, Fs – частота дискретизации. При отображении используют plot(f, abs(Y)), что даёт симметричный спектр вокруг половины частоты дискретизации.

Для получения одностороннего спектра при анализе реальных сигналов используется только первая половина спектра. Необходимо выделить Y(1:N/2+1) и домножить значения амплитуд (кроме первого и последнего) на 2 для корректного отображения энергии. Частотная ось – f = Fs*(0:N/2)/N, построение – plot(f, 2*abs(Y(1:N/2+1))/N). Деление на N обеспечивает нормировку амплитуды.

При анализе важно учитывать окно анализа. Использование оконных функций (hann, hamming) снижает спектральные утечки. Применение окна – x = x .* window(@hann, N) – перед вызовом fft.

Для логарифмического масштаба применяют 20*log10(abs(Y)). При построении спектра мощности используют квадрат модуля abs(Y).^2 или pwelch для усреднения по сегментам.

Точный выбор между односторонним и двусторонним спектром зависит от задачи: визуализация частотного состава – односторонний; анализ фазовых характеристик и комплексной симметрии – двусторонний.

Фильтрация сигнала перед преобразованием Фурье

Перед выполнением преобразования Фурье в MATLAB необходимо удалить из сигнала нежелательные компоненты, искажающие спектр. Фильтрация позволяет устранить шум, подавить помехи и повысить разрешающую способность спектрального анализа.

Для удаления высокочастотных шумов применяйте низкочастотные фильтры. Используйте функцию lowpass с заданной частотой среза, например: filtered = lowpass(signal, 1000, Fs);, где Fs – частота дискретизации.
Для подавления постоянной составляющей перед БПФ рекомендуется использовать фильтр высоких частот: filtered = highpass(signal, 10, Fs);. Это устраняет смещение и улучшает визуализацию спектра на низких частотах.
Для подавления полосовых помех (например, сетевых) эффективны полосовые заграждающие фильтры. Пример: filtered = bandstop(signal, [49 51], Fs); – подавление сетевой частоты 50 Гц.
Используйте функции designfilt и filtfilt для точного управления характеристиками фильтра и минимизации фазовых искажений. Пример: filt = designfilt('lowpassiir','FilterOrder',8,'HalfPowerFrequency',1500,'SampleRate',Fs); filtered = filtfilt(filt, signal);.

Перед фильтрацией важно нормализовать данные и убедиться в отсутствии пропущенных значений (NaN), которые могут вызвать ошибки. Для оценки эффективности фильтрации визуализируйте спектры до и после обработки с помощью fft и plot.

Использование оконных функций для улучшения формы спектра

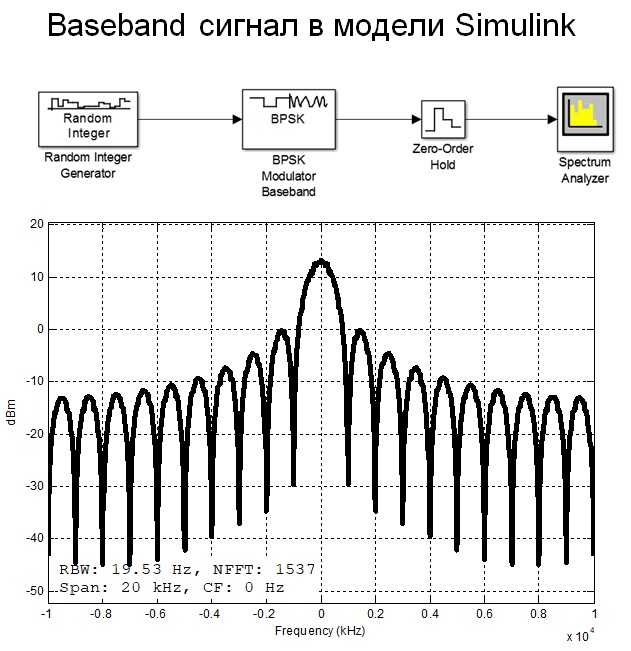
При анализе спектра дискретного сигнала методом БПФ в MATLAB наблюдаются паразитные эффекты, такие как утечка спектра и боковые лепестки. Эти искажения возникают из-за конечной длины анализируемого отрезка сигнала. Для их минимизации применяются оконные функции, которые подавляют амплитуды вне центральной области, уменьшая спектральные искажения.

В MATLAB доступны различные типы окон: Хэмминга, Ханна, Блэкмана, Кайзера и др. Выбор окна зависит от компромисса между шириной главного лепестка и уровнем боковых лепестков. Узкий главный лепесток обеспечивает высокое разрешение, а низкие боковые лепестки – подавление паразитных частот.

Пример применения окна Хэмминга для спектрального анализа:


N = 1024;
x = cos(2*pi*100*(0:N-1)/1000) + 0.5*randn(1,N);
w = hamming(N)';
X = fft(x .* w);
f = (0:N-1)*(1000/N);
plot(f, 20*log10(abs(X)));
xlabel('Частота, Гц'); ylabel('Амплитуда, дБ');

Окно Хэмминга уменьшает боковые лепестки до –43 дБ, при этом ширина главного лепестка составляет примерно 8/N. Если требуется более сильное подавление боковых лепестков, используйте окно Блэкмана (до –74 дБ), но с потерей разрешения.

Для более гибкой настройки применяют окно Кайзера с параметром β. Например, при β = 6.76 боковые лепестки снижаются до –60 дБ, а ширина главного лепестка – около 12/N. Создание окна Кайзера:


beta = 6.76;
w = kaiser(N, beta)';

Использование окон особенно важно при наличии близко расположенных спектральных компонентов. Применение окна позволяет избежать ложных пиков и получить более точную амплитудно-частотную картину сигнала.

Сравнение спектров нескольких сигналов на одном графике

Для точного сопоставления частотных характеристик нескольких сигналов рекомендуется использовать функцию fft совместно с построением графиков через plot или semilogx. Это позволяет выявить различия в спектральном составе и локализовать отличия по частоте.

Пример: задаются два сигнала – синус с частотой 50 Гц и синус с частотой 120 Гц, оба с частотой дискретизации 1000 Гц и длительностью 1 секунда:

Fs = 1000;
t = 0:1/Fs:1-1/Fs;
x1 = sin(2*pi*50*t);
x2 = sin(2*pi*120*t);

Для корректного сравнения необходимо вычислить БПФ одинаковой длины для обоих сигналов:

N = length(t);
X1 = abs(fft(x1, N))/N;
X2 = abs(fft(x2, N))/N;
f = (0:N-1)*(Fs/N);

Отображение выполняется с наложением графиков:

plot(f, X1, 'b', f, X2, 'r');
xlabel('Частота (Гц)');
ylabel('Амплитуда');
legend('Сигнал 1: 50 Гц', 'Сигнал 2: 120 Гц');
xlim([0 200]);

Рекомендация: при отображении нескольких спектров используйте разные цвета и легенду, чтобы избежать путаницы. Устанавливайте ограничение оси xlim по максимально интересующему диапазону частот, чтобы улучшить читаемость. Для сигналов с близкими частотами увеличьте разрешение спектра, применяя нулевое дополнение до большей длины FFT.

Вопрос-ответ:

Как с помощью MATLAB построить спектр дискретного сигнала, полученного в результате синусоидального сигнала с шумом?

Для построения спектра такого сигнала в MATLAB можно воспользоваться функцией `fft`, которая выполняет быстрое преобразование Фурье. Сначала необходимо задать параметры сигнала: частоту дискретизации, длительность, сам сигнал (например, синусоида плюс добавленный шум). Затем применить `fft` к сигналу, вычислить амплитудный спектр и построить график с помощью `plot` или `stem`. Также рекомендуется использовать `fftshift` и нормализацию для корректного отображения симметричного спектра. Визуализация в частотной области поможет оценить наличие шумов и характерную частоту исходного сигнала.

Почему при построении спектра сигнала в MATLAB получается симметричный график?

Симметрия спектра связана с тем, что преобразование Фурье комплексно, а если исходный сигнал — вещественный, его спектр будет обладать так называемой спектральной зеркальной симметрией. Это означает, что вторая половина спектра является зеркальным отражением первой по отношению к середине. В MATLAB массив, возвращаемый `fft`, содержит значения как положительных, так и отрицательных частот, причем отрицательные частоты отображаются во второй половине массива. Если отображается только первая половина спектра (например, при использовании `abs(Y(1:N/2))`), это делает график более наглядным, особенно при анализе физических сигналов, где отрицательные частоты зачастую не имеют практического смысла.