Функция DSolve в Mathematica позволяет находить аналитические решения систем дифференциальных уравнений любого порядка. Например, система {x'[t] == y[t], y'[t] == -x[t]} решается вызовом DSolve[{x'[t] == y[t], y'[t] == -x[t]}, {x, y}, t], что возвращает общее решение в параметрической форме через константы интегрирования.
Для численного анализа используется NDSolve, особенно при отсутствии замкнутого аналитического выражения. Команда NDSolve[{x'[t] == y[t], y'[t] == -x[t], x[0] == 1, y[0] == 0}, {x, y}, {t, 0, 10}] возвращает интерполированные функции, пригодные для построения графиков и дальнейших вычислений.
Работа с системами требует внимательного задания условий: начальные значения указываются в том же списке, что и сами уравнения, и должны быть полными, иначе Mathematica вернёт недоопределённое решение. Переменные и функции должны быть заданы в явном виде; сокращения или пропуски приводят к ошибкам интерпретации.
Для визуализации решений применяются функции Plot и ParametricPlot. В случае двумерной системы удобно использовать ParametricPlot[{x[t], y[t]} /. solution, {t, 0, 10}], где solution – результат NDSolve. Это позволяет исследовать фазовый портрет системы без лишней постобработки данных.
Построение системы уравнений в синтаксисе Mathematica
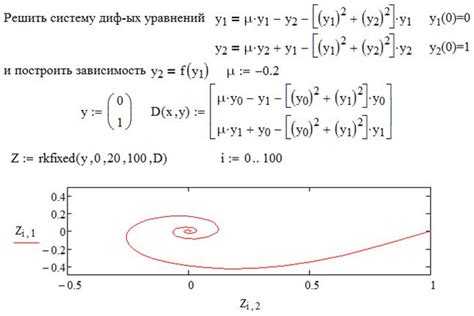
Для задания системы дифференциальных уравнений в Mathematica используется функция Equal (==) и обозначение производных через y'[x], y''[x] и так далее. Независимая переменная указывается явно.
- Используйте
{eq1, eq2, ...}для группировки уравнений в систему. - Каждое уравнение записывается в форме, где левая и правая части связаны оператором
==, а не=. - Переменные должны быть функциями, например
y[x], а не простоy. - Если система включает несколько функций, обозначайте их отдельно:
y[x],z[x],w[x]и т.д.
Пример корректной записи:
eqns = {
y'[x] == z[x],
z'[x] == -y[x],
y[0] == 1,
z[0] == 0
};
В этом примере задана система из двух уравнений второго порядка, переписанная как система первого порядка. Это позволяет использовать стандартные численные методы решения.
Для работы с системой необходимо также указать список функций:
vars = {y, z};
И передать его в функцию NDSolve или DSolve:
NDSolve[{eqns}, vars, {x, 0, 10}]
Если в уравнениях встречаются параметры, например коэффициенты, они должны быть определены явно или оставлены символически, если требуется аналитическое решение.
- Параметры обозначаются как символы:
a,b,ωи т.д. - Для численного решения необходимо присвоить им значения перед вызовом
NDSolve.
Применение функции DSolve для получения аналитического решения

DSolve – ключевая функция в Mathematica для нахождения аналитических решений систем дифференциальных уравнений. Она поддерживает как обыкновенные дифференциальные уравнения (ОДУ), так и системы ОДУ с несколькими неизвестными.
Синтаксис: DSolve[{уравнение1, уравнение2, …}, {переменная1, переменная2, …}, независимая_переменная]. Все уравнения указываются в виде списка, даже если оно одно. Переменные, по которым находятся решения, также должны быть заданы списком.
Для корректной работы DSolve необходимо явно указывать зависимость переменных. Например: y[x], z[x], а не просто y, z. Это позволяет системе распознать производные и правильно обработать дифференцирование.
Если в системе присутствуют начальные условия, они добавляются в список уравнений, например: y[0] == 1. DSolve учитывает их автоматически при поиске общего решения.
Пример: для системы {y'[x] == y[x] + z[x], z'[x] == y[x] — z[x], y[0] == 1, z[0] == 0} вызов DSolve будет выглядеть так: DSolve[{y'[x] == y[x] + z[x], z'[x] == y[x] — z[x], y[0] == 1, z[0] == 0}, {y[x], z[x]}, x].
Если уравнения содержат параметры, Mathematica оставит их в аналитическом выражении. Для упрощения результата используйте Simplify или FullSimplify после получения решения.
Решение возвращается в виде списка правил: {{y[x] -> выражение, z[x] -> выражение}}. Чтобы подставить их в выражение или вывести, примените ReplaceAll (//.) или /. .
При работе с жёсткими или нелинейными системами DSolve может не выдать результат. В таких случаях используйте NDSolve для численного решения или попытайтесь упростить систему вручную.
Использование NDSolve для численного решения с заданными начальными условиями
Функция NDSolve применяется для численного интегрирования систем дифференциальных уравнений при наличии конкретных начальных условий. Синтаксис базовой формы: NDSolve[{\{уравнения\}, \{начальные условия\}}, \{функции\}, \{переменная, нач, кон\}].
Для системы из двух уравнений первого порядка, например:
eqs = {
x'[t] == y[t],
y'[t] == -x[t]
};
init = {
x[0] == 1,
y[0] == 0
};
sol = NDSolve[{eqs, init}, {x, y}, {t, 0, 10}];
Функции x[t] и y[t] будут аппроксимированы на отрезке [0, 10]. Результат – это правило с заменой x и y на интерполированные функции. Для получения значений или визуализации: Plot[Evaluate[x[t] /. sol], {t, 0, 10}].
Рекомендуется всегда указывать диапазон переменной, так как без него решение не вычисляется. При наличии жёстких уравнений желательно использовать метод Method → {"StiffnessSwitching"} или "BDF", например:
sol = NDSolve[{eqs, init}, {x, y}, {t, 0, 10}, Method → {"BDF"}];
Если начальные условия заданы в момент, отличающийся от начала интегрируемого интервала, необходимо явно указать это в уравнениях и диапазоне:
eqs = {
x'[t] == y[t],
y'[t] == -x[t]
};
init = {
x[2] == 0.5,
y[2] == -1
};
sol = NDSolve[{eqs, init}, {x, y}, {t, 2, 10}];
Функция NDSolve не поддерживает неоднозначные или противоречивые начальные условия. Все зависимости должны быть непротиворечивыми и чётко определёнными на начальном отрезке.
Визуализация решений системы с помощью Plot и ParametricPlot
После получения численного решения системы дифференциальных уравнений с помощью функции NDSolve, визуализация возможна с использованием Plot и ParametricPlot для одномерных и фазовых кривых соответственно.
Для отображения зависимостей отдельных переменных от времени используется Plot. Например, при решении системы {x'[t] == y[t], y'[t] == -x[t]} с начальными условиями x[0] == 1, y[0] == 0, вызов будет следующим:
sol = NDSolve[{
x'[t] == y[t],
y'[t] == -x[t],
x[0] == 1,
y[0] == 0
},
{x, y},
{t, 0, 10}
];
Plot[Evaluate[{x[t], y[t]} /. sol], {t, 0, 10}, PlotLegends -> {"x(t)", "y(t)"}]
Для построения фазовой траектории используется ParametricPlot с подстановкой решения в параметрическую кривую {x[t], y[t]}:
ParametricPlot[
Evaluate[{x[t], y[t]} /. sol],
{t, 0, 10},
AxesLabel -> {"x", "y"}
]
Если система содержит более двух переменных, визуализацию фазового пространства можно реализовать через проекции, выбирая пары переменных. Например, для системы из трёх уравнений {x'[t], y'[t], z'[t]} можно построить {x[t], y[t]}, {y[t], z[t]} и {x[t], z[t]}.
При необходимости отображения нескольких траекторий при разных начальных условиях, удобно использовать Table и Show. Например, чтобы сравнить поведение системы при различных значениях x[0]:
plots = Table[
sol = NDSolve[{
x'[t] == y[t],
y'[t] == -x[t],
x[0] == x0,
y[0] == 0
},
{x, y},
{t, 0, 10}
];
ParametricPlot[
Evaluate[{x[t], y[t]} /. sol],
{t, 0, 10}
],
{x0, -2, 2, 0.5}
];
Show[plots]
Для повышения читаемости графиков рекомендуется использовать параметры PlotStyle, PlotRange, AxesLabel, GridLines и AspectRatio. Это позволяет выявить ключевые особенности динамики и облегчает интерпретацию поведения системы.
Обработка систем с параметрами и последующий анализ поведения решений

В Mathematica параметризованные системы задаются с использованием символов, не определённых численно. Для анализа поведения решений при различных значениях параметров удобно использовать функцию DSolve или NDSolve в комбинации с ParametricNDSolve. Последняя позволяет вычислять численные решения систем ОДУ для всего диапазона параметров без пересчёта структуры системы.
Пример: система из двух уравнений с параметром a:
ParametricNDSolve[
{x'[t] == a x[t] - y[t], y'[t] == x[t] + a y[t],
x[0] == 1, y[0] == 0},
{x, y}, {t, 0, 10}, {a}]
Результатом является объект, к которому можно обращаться с подстановкой конкретных значений a. Это позволяет построить траектории в фазовом пространстве для разных режимов системы:
sol = ParametricNDSolve[...];
Plot[
Evaluate[Table[
x[t] /. sol[a -> val][[1]], {val, {-2, 0, 2}}]],
{t, 0, 10}]
Для анализа устойчивости решений при различных параметрах полезно использовать функцию JacobianMatrix из пакета Calculus`VectorAnalysis` или вручную вычислять якобиан и собственные значения. Это позволяет оценить тип стационарных точек и определить наличие бифуркаций при изменении параметров.
Для построения диаграмм бифуркаций применяют Manipulate с визуализацией зависимости решений от параметров. Например, чтобы отследить изменение амплитуды колебаний при варьировании a, используют:
Manipulate[
Plot[Evaluate[x[t] /. sol[a -> val]], {t, 0, 10}],
{val, -3, 3}]
Для локального анализа поведения около особых точек применяют линейное приближение: находят стационарные состояния, подставляют их в якобиан и вычисляют собственные значения. Переход вещественных частей собственных значений через ноль указывает на изменение устойчивости.
В случае жёстких систем или медленно меняющихся параметров эффективны методы продолжения решений, которые можно реализовать через рекурсивный вызов NDSolve с пошаговым изменением параметра и передачей условий на конец предыдущего расчёта.
Работа с системами уравнений высокого порядка и их приведение к первому порядку
Mathematica не поддерживает прямое решение систем дифференциальных уравнений высокого порядка, поэтому перед решением необходимо привести их к системе уравнений первого порядка. Для этого каждый дифференциальный уравнение порядка n разбивается на n уравнений первого порядка с помощью введения вспомогательных переменных, представляющих производные исходной функции.
Например, для уравнения второго порядка y»[x] = f(x, y, y’) вводятся переменные y1[x] = y[x] и y2[x] = y'[x]. Система преобразуется в: y1′[x] = y2[x], y2′[x] = f(x, y1[x], y2[x]). Аналогично для систем с несколькими уравнениями и более высоким порядком.
В Mathematica удобно использовать функцию DSolve или NDSolve для решения преобразованной системы. Для автоматизации разбивки можно определить правила замены или использовать оператор Derivative с введением новых функций.
При реализации важно сохранять согласованность начальных условий: начальные значения для каждой новой переменной устанавливаются исходя из значений функции и её производных. Это критично для численных методов, так как нарушение порядка и соответствия условий приводит к ошибкам и нестабильности.
В случае систем с высоким порядком, особенно при численном решении, рекомендуется дополнительно контролировать шаг интегрирования и оценивать устойчивость метода, что позволяет избежать накапливания ошибок и обеспечивает точность.
Вопрос-ответ:
Как в Mathematica задать систему дифференциальных уравнений для последующего решения?
Для создания системы в Mathematica используют список уравнений с переменными, зависящими от времени или другого параметра. Каждое уравнение записывается в форме производной, например: x'[t] == f(x[t], y[t]), y'[t] == g(x[t], y[t]). Затем эту систему помещают в функцию NDSolve или DSolve, вместе с начальными условиями, чтобы получить решение.
Чем отличаются методы решения системы дифференциальных уравнений в Mathematica: DSolve и NDSolve?
DSolve предназначена для получения аналитических выражений решений, когда это возможно. Она пытается найти формулу в замкнутом виде. NDSolve, в отличие от неё, работает численно и возвращает приближённые значения решения в виде интерполяционной функции. NDSolve полезна при сложных системах, для которых аналитическое решение отсутствует или трудно получить.
Как задать начальные условия для системы дифференциальных уравнений в Mathematica?
Начальные условия вводятся вместе с уравнениями в виде уравнений, задающих значения переменных или их производных в конкретной точке, чаще всего в момент времени t=0. Например: x[0] == 1, y[0] == 0. Эти условия передаются в функции DSolve или NDSolve вместе с системой уравнений для определения конкретного решения.
Можно ли в Mathematica решать системы дифференциальных уравнений с параметрами и как это сделать?
Да, Mathematica позволяет работать с параметрами внутри уравнений. Их можно задать в системе в виде символов и передавать конкретные значения через подстановку или используя опции функций. Часто параметры объявляют как символы, а после решения подставляют нужные числа, либо сразу решают с конкретными значениями параметров.
Как визуализировать решение системы дифференциальных уравнений, полученное в Mathematica?
После численного решения с помощью NDSolve результат обычно представляется в виде интерполяционной функции. Для построения графика применяют Plot или ParametricPlot, передавая в них функции, полученные из решения. Например, Plot[{x[t] /. sol, y[t] /. sol}, {t, t0, t1}] отобразит зависимости переменных по времени. Для фазовых плоскостей используют ParametricPlot.
Как задать систему обыкновенных дифференциальных уравнений для решения в Mathematica?
В Mathematica систему дифференциальных уравнений задают в виде списка уравнений, где каждая функция представлена через переменную и её производные. Например, для функций y1[t] и y2[t] с их производными можно написать: {y1′[t] == f1(t, y1[t], y2[t]), y2′[t] == f2(t, y1[t], y2[t])}. Такой список передают в функцию NDSolve или DSolve вместе с начальными условиями, чтобы получить решение системы.