Mathcad предоставляет удобные инструменты для работы с системами уравнений, позволяя быстро находить решения как для линейных, так и для нелинейных задач. В этой статье рассмотрим основные шаги, которые помогут эффективно задать систему уравнений в Mathcad, не теряя времени на сложные манипуляции с интерфейсом.
Для начала необходимо правильно ввести уравнения. В Mathcad можно использовать обычные математические операторы и функции, при этом важно соблюдать правильный синтаксис. Чтобы задать систему, достаточно ввести несколько уравнений, разделенных символом «=», каждое из которых будет соответствовать одной строке в системе.
Пример: если нужно решить систему уравнений вида ax + by = c и dx + ey = f, то можно ввести следующие выражения в Mathcad:
a*x + b*y = c
d*x + e*y = f
Mathcad автоматически определит переменные и подготовит систему к решению. Для нахождения решений можно использовать функцию linsolve() для линейных систем или воспользоваться solve() для более сложных задач, включая нелинейные уравнения.
Не забывайте проверять корректность введенных значений и следить за правильностью обозначений переменных. В случае с нелинейными системами, также важно указывать начальные приближения, так как метод численного решения может зависеть от этих значений.
Подготовка среды для работы с системой уравнений в Mathcad

Для эффективной работы с системой уравнений в Mathcad необходимо правильно настроить рабочее пространство и использовать ключевые возможности программы. Во-первых, создайте новый документ, выбрав соответствующий шаблон. Mathcad позволяет работать с несколькими рабочими листами, что дает гибкость при решении разных групп уравнений. Для этого в верхнем меню выберите опцию «Файл» и затем «Новый».
Важно убедиться, что в настройках программы включены все необходимые математические функции и библиотеки. В Mathcad доступны различные расширения, такие как дополнительные математические пакеты и функции для решения систем нелинейных уравнений, интегралов и дифференциальных уравнений. Для загрузки этих расширений воспользуйтесь меню «Справка» и пунктом «Установить дополнительные библиотеки».
Работа с системой уравнений требует четкой структуры, поэтому лучше всего разбить задачи на несколько разделов. В Mathcad можно использовать разметку для добавления текстовых пояснений и обозначений, что помогает структурировать решение. Для этого в меню «Вставка» выберите «Текст», а затем используйте удобное форматирование для выделения различных частей работы.
Для решения системы линейных уравнений воспользуйтесь встроенной функцией «linsolve». Она позволяет найти решения для неизвестных переменных с использованием матричных методов. Для этого введите коэффициенты системы в виде матрицы и задайте вектор правых частей. В случае системы нелинейных уравнений лучше использовать итерационные методы, такие как метод Ньютона, доступный в Mathcad.
Настройка числовых форматов также имеет значение. При работе с системой уравнений часто требуются точные вычисления. В Mathcad можно установить необходимую точность вычислений в параметрах документа, что позволит избежать погрешностей. Перейдите в меню «Инструменты» и выберите «Параметры», чтобы настроить точность вычислений и формат отображения чисел.
Кроме того, стоит настроить автоматическую проверку на ошибки и синтаксические ошибки. Для этого в настройках программы активируйте «Проверку синтаксиса». Это поможет избежать случайных ошибок при вводе сложных уравнений, что особенно важно при решении многозначных задач.
Создание и ввод линейных уравнений в Mathcad
Для создания и ввода линейных уравнений в Mathcad необходимо понимать, как правильно форматировать математические выражения. Линейные уравнения в Mathcad могут быть заданы с помощью стандартных математических операторов и переменных. Чтобы ввести линейное уравнение, используйте символы для операций сложения, вычитания, умножения и деления. Например, уравнение вида «2x + 3y = 5» вводится как:
2*x + 3*y = 5
Для задания системы линейных уравнений необходимо прописать несколько выражений, каждое из которых будет содержать одну строку с уравнением. Mathcad автоматически распознает и будет работать с ними как с системой уравнений, если уравнения разделены на разные строки. Например, систему уравнений можно записать следующим образом:
2*x + 3*y = 5
4*x — y = 3
Важно помнить, что переменные в Mathcad не нужно заранее объявлять, но их нужно задать перед решением системы уравнений. Чтобы решить систему, используйте команду «Solve» (или клавишу Ctrl + Shift + =). Программа автоматически решит систему по умолчанию для всех переменных, входящих в уравнение.
Mathcad позволяет легко использовать параметры для решения более сложных систем, где необходимо учесть дополнительные условия. Например, чтобы решить систему с двумя неизвестными, можно задать уравнения и решить их с помощью функции «Solve», как показано ниже:
2*x + 3*y = 5
4*x — y = 3
Используя «Solve», можно быстро найти значения переменных x и y, подставив их в уравнения. Для более точных расчетов можно также использовать различные типы разреженных и плотных матриц в качестве входных данных для системы уравнений, в зависимости от требуемой задачи.
Работа с нелинейными уравнениями в Mathcad
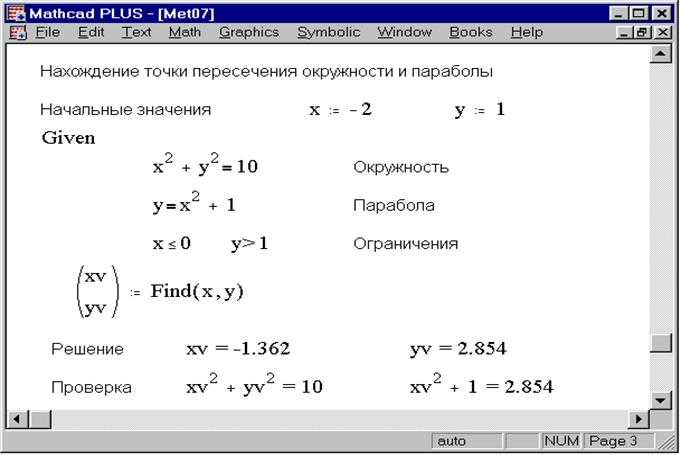
Для задания нелинейного уравнения в Mathcad необходимо просто ввести его в виде математического выражения. Например, для уравнения вида x^2 - 5*x + 6 = 0, необходимо записать его как x^2 - 5*x + 6. После этого можно применить функцию решения, такую как solve или fsolve.
Для решения нелинейных уравнений, которые не могут быть решены аналитически, используется функция fsolve. Она принимает начальные приближения для переменных и решает уравнение с заданной точностью. Пример использования: fsolve(x^2 - 5*x + 6, x, 1) – это решение уравнения при начальном приближении для x равном 1.
При работе с нелинейными уравнениями важно учитывать начальные условия. Если выбрать неправильные начальные приближения, можно получить ошибочные результаты или не решить уравнение вообще. В таких случаях рекомендуется проверять решение, изменяя начальные приближения и анализируя поведение функции в разных точках.
Для систем нелинейных уравнений используется расширенная версия fsolve, где на вход подается система уравнений. Например, для системы уравнений x^2 + y^2 = 1 и x - y = 0, решение будет следующим: fsolve({x^2 + y^2 - 1, x - y}, {x, y}, {0.5, 0.5}), где {0.5, 0.5} – начальное приближение для x и y.
Mathcad также позволяет строить графики для визуализации решений нелинейных уравнений. Это помогает проанализировать поведение функции и выбрать более подходящее начальное приближение для fsolve. Графики часто используются для подтверждения корректности решения, особенно если у уравнения несколько решений.
В дополнение к стандартным функциям решения, Mathcad предоставляет возможности для работы с параметрическими уравнениями, где переменные могут зависеть от других величин. Это полезно при решении более сложных нелинейных задач, например, в инженерных расчетах или при моделировании динамических систем.
Нелинейные уравнения могут быть решены и с использованием метода Ньютона, который реализован в Mathcad через функцию newton. Этот метод подходит для уравнений, для которых известна производная функции, и требует меньше вычислительных ресурсов при высоких точностях.
Решение системы уравнений методом подбора значений
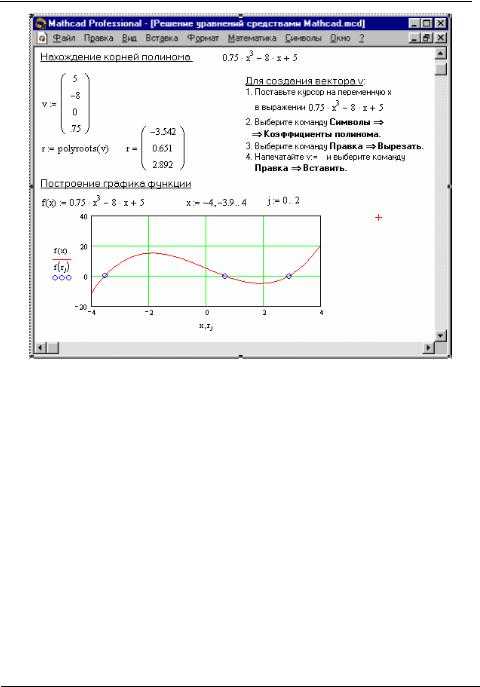
Метод подбора значений заключается в последовательном пробном подставлении различных значений переменных, чтобы найти такие, при которых система уравнений будет удовлетворена. Это может быть эффективным инструментом при решении нелинейных систем, когда аналитическое решение затруднительно или невозможно.
Для начала следует установить диапазоны значений переменных. Например, если система уравнений содержит переменные \(x\) и \(y\), необходимо предварительно определить их возможные пределы на основе физического смысла задачи или других ограничений. В Mathcad можно использовать функцию подбора значений, применяя итеративный процесс для нахождения решений.
Основной принцип метода заключается в том, что при каждой итерации подбираются значения переменных и подставляются в систему уравнений. Если система уравнений не выполнена, пробуются другие значения. Этот процесс продолжается до тех пор, пока не будет найдено приближённое решение.
В Mathcad решение начинается с создания уравнений и определения переменных. Для этого можно использовать встроенные функции, такие как fsolve для численного решения уравнений. В случае с методом подбора значений следует подготовить список значений переменных и поочередно подставлять их в уравнения с помощью цикла. Важно настроить шаг подбора значений, чтобы процесс поиска не затянулся на слишком долгое время.
Для повышения точности можно уменьшить шаг подбора значений и использовать более точные методы аппроксимации, например, метод деления пополам или метод Ньютона, если система уравнений это позволяет.
Метод подбора значений эффективен при небольших системах уравнений с ограниченным числом переменных. Для более сложных задач лучше использовать численные методы оптимизации или специализированные алгоритмы решения системы уравнений, чтобы ускорить процесс и повысить точность.
Использование встроенных функций для решения системы уравнений

В Mathcad для решения системы уравнений можно использовать встроенные функции, такие как linsolve() и fsolve(), которые позволяют эффективно находить значения переменных, удовлетворяющих системе уравнений. Эти функции оптимизированы для различных типов задач и предоставляют пользователю удобный интерфейс для работы с матрицами и нелинейными уравнениями.
Функция linsolve() используется для решения линейных систем уравнений. Она принимает матрицу коэффициентов и вектор правых частей, возвращая решение системы в виде вектора значений переменных. Например:
linsolve(A, b)
Где A – это матрица коэффициентов, а b – вектор правых частей. Для системы из двух уравнений с двумя переменными пример использования будет следующим:
A := {{3, -1}, {2, 4}} // Матрица коэффициентов
b := {7, 10} // Вектор правых частей
x := linsolve(A, b) // Результат: {x1, x2}
Для решения нелинейных систем уравнений можно использовать функцию fsolve(). Эта функция применяет численные методы для нахождения корней нелинейных уравнений. В отличие от linsolve(), fsolve() требует начальных приближений для переменных. Пример использования:
fsolve({eq1, eq2}, {x1_guess, x2_guess})
Где eq1 и eq2 – это уравнения системы, а x1_guess и x2_guess – начальные приближения для переменных. Например:
eq1 := x1^2 + x2^2 - 4 // Первое уравнение
eq2 := x1*x2 - 1 // Второе уравнение
solution := fsolve({eq1, eq2}, {1, 1}) // Начальные приближения: x1 = 1, x2 = 1
Для более сложных задач, где требуется решить систему с большим количеством уравнений и переменных, рекомендуется использовать функции с дополнительными параметрами, такие как точность решения или максимальное количество итераций. Эти параметры позволяют контролировать процесс решения и минимизировать погрешности.
Важным аспектом является выбор метода решения в зависимости от характеристик системы уравнений. Для линейных систем с четкой структурой предпочтительнее использовать linsolve(), а для более сложных нелинейных задач – fsolve(), учитывая возможность настройки начальных приближений и параметров решения.
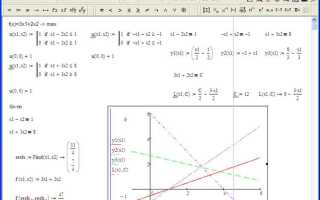
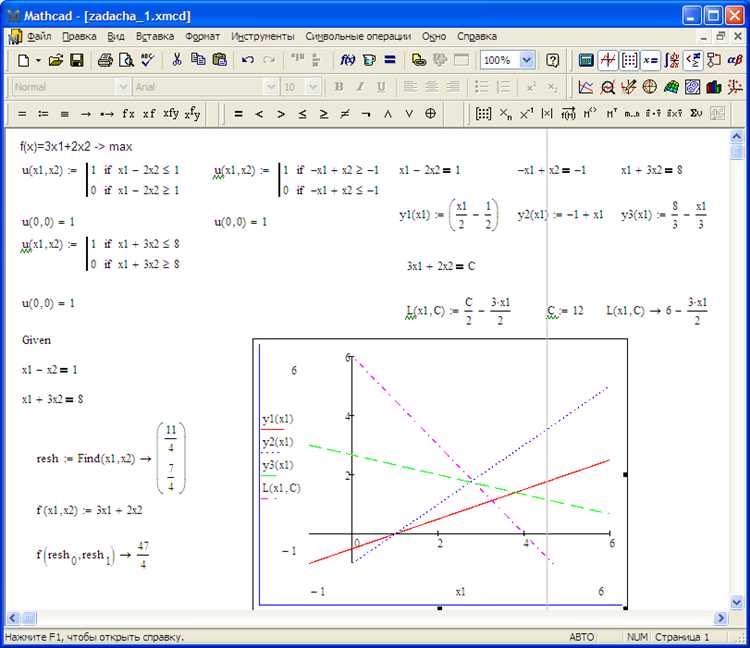
Построение графиков для визуализации решения системы уравнений

Чтобы построить график системы уравнений в Mathcad, необходимо выполнить несколько шагов:
- Шаг 1: Определение функций системы. Задать уравнения в виде функций, например,
f(x)иg(x). - Шаг 2: Построение графиков этих функций. Для этого используйте команду
plotили инструменты для графиков в Mathcad. Например, для отображения функции можно использовать такую конструкцию:plot(f(x), x, -10, 10). - Шаг 3: Добавление графиков других уравнений. Можно наложить на один график несколько функций, чтобы увидеть точки пересечения. Для этого используйте следующую форму:
plot(f(x), g(x), x, -10, 10).
Графическое отображение системы уравнений в Mathcad позволяет:
- Визуализировать точки пересечения, которые являются решениями системы.
- Оценить, как изменения в параметрах уравнений влияют на результаты.
- Получить точное представление о поведении функций в различных диапазонах.
Для точности построения графика рекомендуется использовать различные диапазоны значений переменных и масштабирование осей, чтобы лучше увидеть пересечения. Важно также указать сетку для лучшего ориентирования на графике.
Если система уравнений нелинейная, можно воспользоваться числовыми методами для нахождения корней функций, например, методом Ньютона или методами, встроенными в Mathcad для численного решения уравнений.
Для более сложных случаев, когда система уравнений включает несколько переменных, можно построить графики в трехмерном пространстве с помощью инструмента 3D Plot. Это позволяет получить точное представление о многомерных решениях системы.
Наглядное представление с помощью графиков делает решение системы уравнений более интуитивно понятным, облегчая анализ результатов и выявление закономерностей.
Вопрос-ответ:
Как в Mathcad задать систему уравнений для решения?
Для того чтобы задать систему уравнений в Mathcad, нужно использовать стандартный синтаксис языка, доступный в программе. Например, если требуется решить систему из двух уравнений с двумя переменными, нужно ввести каждое уравнение на отдельной строке. На каждой строке следует указать переменные и их зависимости. Для решения системы используйте команду `solve`, которая поможет найти значения переменных, при которых оба уравнения выполняются одновременно. Важно правильно расставить скобки и знаки равенства, чтобы Mathcad корректно обработал введенную информацию. Также стоит помнить, что Mathcad позволяет работать с линейными и нелинейными системами уравнений.