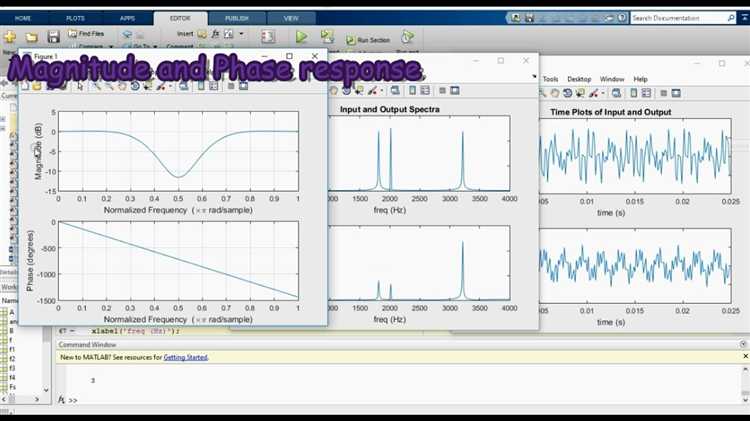
Фильтрация сигналов в среде Matlab – ключевая задача при обработке цифровых данных. В этой статье рассматривается построение фильтров с использованием встроенных функций filter, designfilt и инструментов Filter Designer. Особое внимание уделяется практическому синтезу фильтров низких, высоких и полосовых частот с зафиксированными параметрами: частотой среза, порядком и типом оконной функции.
Начнем с создания фильтра низких частот FIR с помощью функции fir1. Предположим, частота дискретизации составляет 8000 Гц, частота среза – 1000 Гц, порядок фильтра – 50. В Matlab это реализуется командой: b = fir1(50, 1000/4000);. Результат – вектор коэффициентов фильтра, который может быть применён к сигналу через filter(b,1,x), где x – входной сигнал.
Для более точного управления характеристиками применяют designfilt. Например, полосовой фильтр с полосой пропускания 500–1500 Гц и частотой дискретизации 8000 Гц можно сконструировать так: d = designfilt(‘bandpassfir’,’FilterOrder’,60,’CutoffFrequency1′,500,’CutoffFrequency2′,1500,’SampleRate’,8000);. Этот метод обеспечивает доступ к множеству параметров, включая тип оконной функции и амплитудно-частотные ограничения.
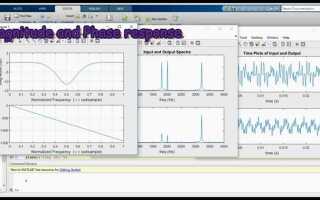
Графический инструмент Filter Designer позволяет визуализировать амплитудно-частотные характеристики и изменять параметры фильтра в реальном времени. Он особенно полезен при проектировании IIR-фильтров (Butterworth, Chebyshev, Elliptic). Запускается командой filterDesigner. После настройки всех параметров фильтр можно экспортировать в рабочее пространство для дальнейшего анализа или применения к сигналу.
В статье далее разбираются конкретные примеры применения, включая фильтрацию ЭКГ-сигналов и аудио данных. Каждый шаг сопровождается комментариями по выбору оптимальных параметров в зависимости от требований к фазовому сдвигу, амплитудным искажениям и вычислительным затратам.
Создание фильтров в Matlab: пошаговое руководство
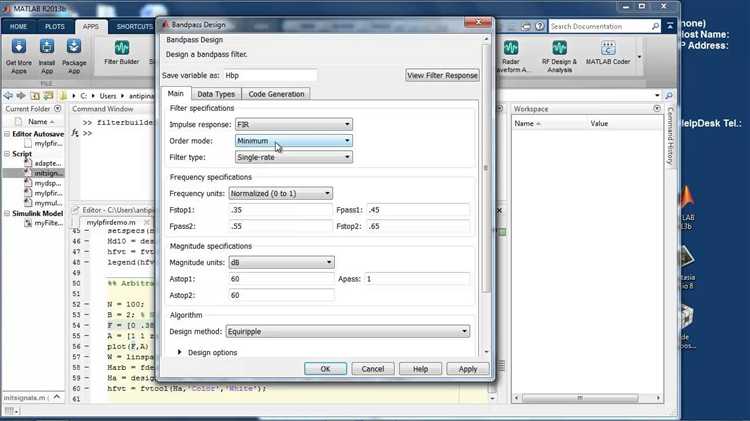
1. Откройте среду Matlab и перейдите к инструменту Filter Designer, выполнив команду filterDesigner в командном окне.
2. В открывшемся окне выберите тип фильтра в поле Response Type: низкочастотный (Lowpass), высокочастотный (Highpass), полосовой (Bandpass) или режекторный (Bandstop).
3. Укажите метод проектирования в разделе Design Method. Для цифровых фильтров IIR доступны алгоритмы Butterworth, Chebyshev I/II и Elliptic. Для FIR – методы типа window-based или equiripple.
4. Введите параметры фильтра:
- Порядок фильтра (Filter Order) – влияет на крутизну характеристики. Пример: 6 для IIR или 30 для FIR.
- Частоты среза (Cutoff Frequencies) – указываются в нормализованной форме (0–1), где 1 соответствует половине частоты дискретизации.
- Частота дискретизации (Fs) – указывается в Гц, например: 48000.
- Допустимые пульсации и затухания – применяются для фильтров Чебышёва и эллиптических (например, Ripple = 0.5 дБ, Attenuation = 40 дБ).
5. Нажмите Design Filter, чтобы построить фильтр. Перейдите к вкладке Analysis и выберите нужные графики: амплитудно-частотная характеристика, фазовая характеристика, задержка группы и импульсная характеристика.
6. Сохраните фильтр в рабочем пространстве: выберите File → Export, укажите переменную, например Hd, и нажмите Export.
7. Примените фильтр к сигналу с помощью команды:
y = filter(Hd, x);где x – входной сигнал, y – отфильтрованный результат.
8. Для получения коэффициентов фильтра используйте:
[b, a] = tf(Hd);9. Для генерации кода фильтра в виде MATLAB-функции выберите File → Generate MATLAB Code.
10. Рекомендуется проверять стабильность и фазовые искажения. Для IIR фильтров анализируйте полюс-нуля график: вызовите zplane(Hd). Для FIR – убедитесь в линейной фазе через phasez(Hd).
Определение требований к фильтру: тип, порядок, полоса пропускания
Перед созданием фильтра в MATLAB необходимо точно задать его параметры. Начните с выбора типа фильтра: низкочастотный (LPF), высокочастотный (HPF), полосовой (BPF) или режекторный (BSF). Тип фильтра зависит от того, какие частоты требуется подавить или сохранить.
Для низкочастотного фильтра задаются максимальная частота пропускания и частота среза. Например, для аудиосигнала может потребоваться LPF с полосой пропускания до 3 кГц и полосой заграждения от 3.5 кГц. Для полосового фильтра указываются нижняя и верхняя границы пропускания, например, 1–2 кГц, а также ширина переходной области.
Определите порядок фильтра. Более высокий порядок обеспечивает более резкий спад в полосе заграждения, но увеличивает вычислительную нагрузку и может вызвать фазовые искажения. Для большинства задач подходит порядок от 4 до 8. Если требуется очень крутой фронт спада, рассмотрите порядок 10 и выше, но предварительно проверьте устойчивость системы.
Полоса пропускания и переходные области должны быть выражены в нормализованных частотах (от 0 до 1), где 1 соответствует половине частоты дискретизации. Например, при Fs = 8000 Гц, полоса до 2 кГц будет соответствовать нормализованной частоте 0.5.
Четко определённые параметры фильтра позволяют использовать встроенные функции MATLAB, такие как designfilt или butter, без лишнего подбора. Это ускоряет разработку и повышает точность обработки сигнала.
Проектирование цифрового фильтра с использованием функции fdatool
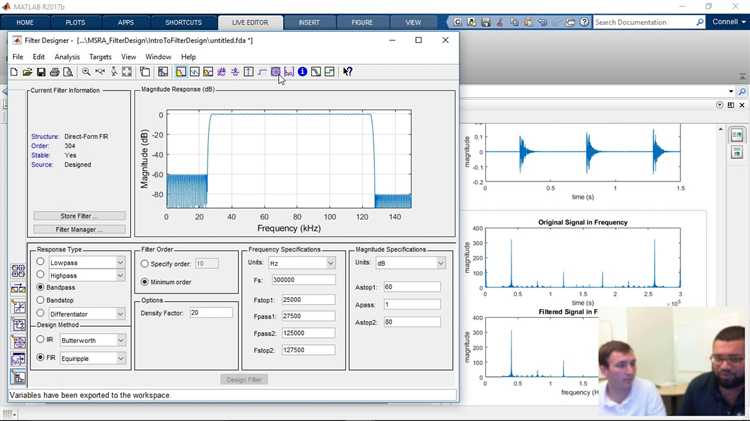
Откройте командное окно MATLAB и введите fdatool для запуска графического интерфейса Filter Design and Analysis Tool. В появившемся окне выберите тип фильтра: Lowpass, Highpass, Bandpass или Bandstop.
В разделе Response Type выберите форму фильтра. Затем укажите метод проектирования: Butterworth, Chebyshev Type I, Chebyshev Type II или Elliptic – в зависимости от требований к фазовым и амплитудным искажениям.
Перейдите к параметрам фильтра. Задайте частоты отсечки в поле Frequency Specifications. Частоты указываются в нормализованном виде: 1 соответствует половине частоты дискретизации. Например, для фильтра низких частот с частотой среза 3 кГц и частотой дискретизации 10 кГц введите 0.6.
Задайте параметры полосы пропускания и подавления: Passband Ripple и Stopband Attenuation. Например, для 1 дБ пульсации в полосе пропускания и 60 дБ подавления указываются значения 1 и 60 соответственно.
Нажмите Design Filter. В нижней части окна отобразится график АЧХ. Для анализа характеристик нажмите Analysis и выберите, например, Magnitude Response или Phase Response.
Чтобы экспортировать фильтр в рабочее пространство, нажмите File → Export. В появившемся окне выберите переменную, например Hd, и убедитесь, что установлен флажок Export to Workspace. Нажмите Export.
После экспорта вы можете применять фильтр к сигналам, используя функцию filter(Hd, x), где x – входной сигнал.
Реализация фильтра через команду designfilt

Команда designfilt используется для проектирования цифровых фильтров с заданными характеристиками. Она позволяет точно контролировать параметры фильтра без необходимости вручную вычислять коэффициенты.
Для создания фильтра нижних частот с частотой среза 1 кГц и частотой дискретизации 8 кГц используется следующий код:
lpFilt = designfilt('lowpassiir', ...
'FilterOrder', 8, ...
'PassbandFrequency', 1000, ...
'PassbandRipple', 0.2, ...
'SampleRate', 8000);Ключевые параметры:
'lowpassiir'– тип фильтра, в данном случае IIR-фильтр нижних частот;'FilterOrder'– порядок фильтра, определяет крутизну спада;'PassbandFrequency'– частота пропускания в Гц;'PassbandRipple'– допустимые колебания в полосе пропускания в дБ;'SampleRate'– частота дискретизации сигнала.
Проверка частотной характеристики фильтра выполняется командой:
fvtool(lpFilt)Для применения фильтра к сигналу используйте:
y = filter(lpFilt, x);Команда designfilt поддерживает широкий набор типов фильтров: 'highpassiir', 'bandpassiir', 'bandstopiir', FIR-варианты и другие. Для получения списка доступных настроек используйте:
help designfiltПри разработке фильтра важно согласовывать параметры с реальными характеристиками сигнала, особенно частоту дискретизации и допустимые искажения. Команда designfilt обеспечивает гибкость и точность при проектировании, позволяя сконцентрироваться на характеристиках фильтра без необходимости ручного подбора коэффициентов.
Применение фильтра к сигналу с помощью функции filter
Функция filter в MATLAB используется для применения цифрового фильтра, заданного коэффициентами, к входному сигналу. Фильтр задаётся в форме разностного уравнения:
y = filter(b, a, x)b– вектор коэффициентов числителя (перед Z-1) передаточной функции фильтра.a– вектор коэффициентов знаменателя.x– входной сигнал.y– отфильтрованный выходной сигнал.
Если a(1) ≠ 1, все коэффициенты b и a необходимо нормализовать на a(1) до вызова filter.
Пример применения фильтра нижних частот 5-го порядка, созданного с использованием функции butter:
[b, a] = butter(5, 0.4); % Фильтр нижних частот, частота среза 0.4 (от нормированной Nyquist)
x = randn(1, 1000); % Исходный шумовой сигнал
y = filter(b, a, x); % Применение фильтраРекомендации:
- При фильтрации коротких сигналов предпочтительнее использовать
filtfilt, чтобы избежать искажений на границах. - Перед фильтрацией убедитесь, что сигнал не содержит выбросов, которые могут усилиться в процессе фильтрации.
- Для анализа отклика фильтра на единичный импульс используйте:
impz(b, a). - Если необходимо сохранить фазу сигнала, используйте нулевую фазовую фильтрацию:
y = filtfilt(b, a, x).
Функция filter применяет фильтр в прямом направлении с инициализацией нулями, что может вызвать артефакты в начале сигнала. Это особенно важно при работе с медленно меняющимися компонентами или постоянной составляющей.
Анализ частотных характеристик с использованием fvtool
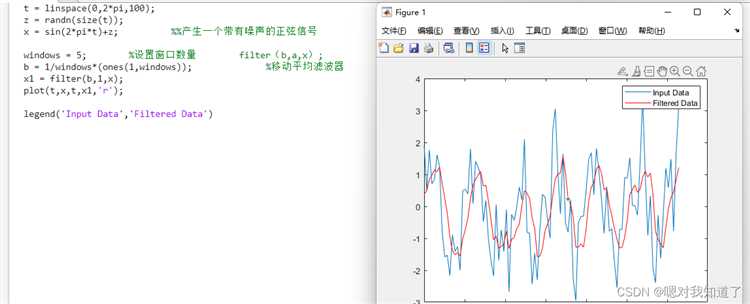
Для анализа фильтра в Matlab после его создания используется функция fvtool, которая позволяет визуализировать амплитудно-частотные, фазовые и импульсные характеристики, а также групповую задержку и отклик на ступенчатое воздействие.
Для запуска анализа выполните команду fvtool(d), где d – объект фильтра, созданный, например, с помощью designfilt или fir1. Если фильтр задан вектором коэффициентов, используйте fvtool(b, a), где b и a – числитель и знаменатель передаточной функции соответственно.
Для включения определённых графиков примените аргументы: 'Analysis','magnitude' для АЧХ, 'Analysis','phase' для фазовой, 'Analysis','grpdelay' для групповой задержки. Например, fvtool(d, 'Analysis', 'grpdelay') покажет график групповой задержки, позволяющий оценить фазовые искажения.
Для сравнения нескольких фильтров передайте их в fvtool через запятую: fvtool(d1, d2). Это удобно при оптимизации параметров фильтрации. Используйте legend в командном окне, чтобы задать подписи: legend('Фильтр 1', 'Фильтр 2').
Настраивайте отображение через графический интерфейс fvtool: масштаб по оси частот, тип шкалы (линейная или логарифмическая), отображение сетки. Это критично при анализе фильтров с узкой полосой пропускания или резким спадом в полосе подавления.
Для экспорта данных используйте меню «File» → «Export» или сохраните график программно: saveas(gcf, 'plot.png').
Сохранение и повторное использование параметров фильтра в проекте
Для сохранения настроек фильтра в MATLAB используйте команду save, чтобы экспортировать структуру фильтра в .mat-файл. Например, после проектирования фильтра с помощью designfilt выполните save('lowpass_filter.mat', 'Hd'), где Hd – переменная фильтра.
Для повторного использования фильтра загрузите его с помощью load: load('lowpass_filter.mat'). Это восстановит объект фильтра Hd, который можно немедленно применять к сигналам через filter(Hd, signal).
Если фильтр создан в Filter Designer, выберите меню File → Export и укажите переменную для workspace. Затем сохраните её в .mat-файл, как описано выше. Чтобы загрузить параметры в Filter Designer, используйте File → Import.
Для пакетной обработки или интеграции фильтра в автоматические скрипты сохраните параметры в структуре, включая тип фильтра, порядок, частоты и коэффициенты. Пример: params = struct('Type','lowpass','Order',8,'Fs',48000,'Fpass',5000);. В дальнейшем используйте их при вызове designfilt через filt = designfilt('lowpassiir','FilterOrder',params.Order,'PassbandFrequency',params.Fpass,'SampleRate',params.Fs).
Вопрос-ответ:
Какой тип фильтра лучше использовать для удаления низкочастотного шума из сигнала?
Для удаления низкочастотного шума обычно применяют фильтр верхних частот (high-pass filter). Он пропускает компоненты сигнала выше заданной частоты среза и подавляет те, что ниже. В Matlab такой фильтр можно спроектировать с помощью функций `designfilt` или `butter`, а затем применить к сигналу с помощью `filter` или `filtfilt`. Частоту среза следует подбирать с учётом спектра полезного сигнала и шума.
Можно ли в Matlab создать фильтр с пользовательскими характеристиками вручную, а не через встроенные функции?
Да, можно. В Matlab допускается задание коэффициентов фильтра вручную, если известны значения числителя и знаменателя передаточной функции. Такие фильтры создаются через команды `filter(b, a, x)`, где `b` и `a` — векторы коэффициентов. Это удобно, когда есть теоретически выведенные параметры или нужно реализовать нестандартную фильтрацию.
Что делает команда `filtfilt` и чем она отличается от `filter`?
Команда `filtfilt` выполняет фильтрацию в двух направлениях: сначала вперёд, затем в обратную сторону. Благодаря этому устраняется фазовое искажение, характерное для обычной фильтрации. В отличие от неё, функция `filter` работает в одном направлении и может вызывать сдвиг фаз в сигнале. Если требуется сохранить форму сигнала, особенно в задачах анализа, предпочтительнее использовать `filtfilt`.
Как задать фильтр с плавающей полосой пропускания в Matlab?
Фильтр с плавающей полосой пропускания можно реализовать программно, изменяя параметры фильтра в процессе обработки данных. Например, можно использовать адаптивные фильтры, такие как `adaptfilt.lms`, которые изменяют свои характеристики в зависимости от входного сигнала. Также можно обновлять параметры обычного фильтра на каждом шаге, если известна функция смещения полосы.