Как дискретизировать сигнал в mathcad

Дискретизация сигналов – ключевой этап при цифровой обработке, позволяющий перейти от непрерывного к дискретному представлению данных. В Mathcad этот процесс реализуется с помощью встроенных функций и операторов, обеспечивающих точное управление частотой выборки и интерполяцией.

Оптимальный выбор метода дискретизации зависит от характера сигнала и требований к точности. Например, для периодических сигналов эффективна равномерная дискретизация с использованием функции sample(), позволяющей задавать интервал и количество точек. В случае шумных или нестационарных сигналов рекомендуется применять адаптивные подходы с динамическим изменением шага дискретизации, что снижает влияние искажений.

Mathcad поддерживает синтез и анализ дискретных сигналов, включая методы линейной интерполяции и фильтрации, что упрощает подготовку данных для дальнейших вычислений. Важным аспектом является соблюдение условия Найквиста для предотвращения алиасинга, что достигается подбором минимальной частоты дискретизации вдвое выше максимальной частоты сигнала.

Использование Mathcad для дискретизации позволяет автоматизировать вычислительные процессы и снизить ошибки ручного ввода, при этом расширяя возможности анализа благодаря визуализации и встроенным математическим инструментам.

Настройка параметров дискретизации в Mathcad

Для задания параметров дискретизации создайте в Mathcad вектор временных точек с помощью функции диапазона, например, t := 0, dt .. T, где 0 – начальный момент, dt – шаг, T – конечное время. Рекомендуется выбирать dt так, чтобы частота дискретизации была минимум в два раза выше максимальной частоты спектра сигнала согласно теореме Найквиста.

Увеличение dt снижает точность и приводит к эффекту наложения спектров (aliasing), уменьшение – повышает детализацию, но увеличивает объем вычислений. Оптимальный выбор определяется балансом между точностью и производительностью.

В Mathcad для анализа дискретных сигналов используйте встроенные функции, например, встроенную функцию fft для преобразования Фурье, где длина выборки должна быть степенью двойки. Для этого удобна настройка количества точек N := (T/dt) с округлением до ближайшей степени двойки.

Для корректного представления непрерывных сигналов важно провести предварительное аппроксимирование функции с учетом выбранного dt, используя операторы интерполяции и проверки гладкости. Это минимизирует погрешности, вызванные дискретизацией.

Применение функции sampling для создания выборок

Функция sampling в Mathcad используется для формирования дискретных выборок из непрерывных сигналов с заданным шагом дискретизации. Вызов sampling требует указания исходной функции, интервала и частоты дискретизации, что позволяет получить массив значений, соответствующих точкам выборки.

Для корректного использования sampling необходимо точно определить интервал дискретизации, который должен соответствовать требованиям теоремы Котельникова-Шеннона – частота дискретизации должна быть не менее удвоенной максимальной частоты спектра сигнала. В Mathcad задают параметры функции следующим образом: sampling(<функция>, <начало интервала>, <конец интервала>, <шаг дискретизации>).

Практическая рекомендация – выбирать шаг дискретизации с учетом быстродействия дальнейших вычислений и точности аппроксимации. Слишком малый шаг ведет к избыточному объему данных и замедлению обработки, слишком большой – к потере информации и искажениям. Оптимальный выбор определяется анализом спектра исходного сигнала и требованиями к точности моделирования.

После создания выборки с помощью sampling полученные данные можно напрямую использовать для построения графиков, проведения спектрального анализа или дальнейшей цифровой обработки. В Mathcad удобно использовать полученный массив с функциями interpolate и fft для получения гладкой аппроксимации и анализа частотных характеристик.

Важно учитывать, что sampling работает с числовыми функциями и требует, чтобы исходный сигнал был определен аналитически или представлен в виде функции Mathcad. Для сложных сигналов, заданных экспериментальными данными, предварительно выполняется интерполяция, после чего sampling применяется к полученной функции.

Реализация равномерной дискретизации сигналов

В Mathcad равномерная дискретизация достигается за счёт задания постоянного шага по времени при создании вектора дискретных отсчётов. Для этого используется оператор диапазона с фиксированным шагом: t := 0, Δt .. T, где Δt – период дискретизации, а T – конечное время сигнала.

Выбор Δt определяется частотой дискретизации f_s = 1/Δt, которая должна вдвое превышать максимальную частоту сигнала согласно теореме Найквиста. Для корректной обработки в Mathcad рекомендуется предварительно анализировать спектр сигнала с помощью встроенных функций преобразования Фурье.

Далее дискретный сигнал строится как массив значений исходной функции, вычисленных в точках t. Например, x := sin(2πf t), где f – частота исходного сигнала. В Mathcad возможно использование функций с векторным аргументом для массового вычисления.

Важно учитывать, что шаг Δt должен быть кратен единице измерения времени модели, иначе возникает риск накопления ошибки округления. Рекомендуется явно задавать параметры типа времени и единицы измерения.

Для повышения точности дискретизации и уменьшения эффекта aliasing перед дискретизацией часто применяют цифровые фильтры нижних частот, реализуемые в Mathcad через свёртку или встроенные библиотеки обработки сигналов.

Обработка несвязных и разреженных сигналов

Несвязные и разреженные сигналы характеризуются отсутствием непрерывной информации во временной области и наличием значительных интервалов с нулевыми или близкими к нулю значениями. В Mathcad для их анализа и обработки применяют методы, учитывающие специфику дискретизации и интерполяции.

Основной задачей является сохранение информативных участков при минимизации влияния пропусков и шумов. Рекомендуется использовать адаптивное разбиение временной оси с переменным шагом, что позволяет увеличить плотность дискретизации в зонах активности сигнала и снизить ее в паузах.

Для восстановления пропущенных значений целесообразно применять методы сплайновой интерполяции и аппроксимации, доступные в Mathcad, обеспечивающие гладкость и точность приближения без излишней осцилляции. При этом следует контролировать порядок сплайна, чтобы избежать переобучения и потери важной динамики.

В задачах анализа разреженных сигналов эффективна фильтрация с использованием пороговых функций, позволяющая отделять значимые импульсы от шума. Mathcad поддерживает построение пороговых фильтров, где значения ниже заданного уровня обнуляются, что улучшает соотношение сигнал/шум без искажения ключевых параметров.

При дискретизации несвязных сигналов важно обеспечить точную синхронизацию и временную маркировку выборок. Mathcad позволяет реализовать синхронизацию с опорными тактовыми сигналами и производить последующий анализ по временным меткам, что особенно важно в мультисенсорных системах.

Использование встроенных функций Mathcad для спектрального анализа позволяет выявлять частотные компоненты даже при наличии разрывов. Применение оконных функций (Ханна, Хэмминга) снижает влияние оконных артефактов и повышает разрешение спектра.

Для повышения точности обработки рекомендуется сочетать методики временного и частотного анализа, комбинируя результаты для формирования более полной картины сигнала. В Mathcad интеграция этих методов реализуется через последовательное применение стандартных функций с последующим графическим сравнением.

Использование временных и частотных шкал в дискретизации

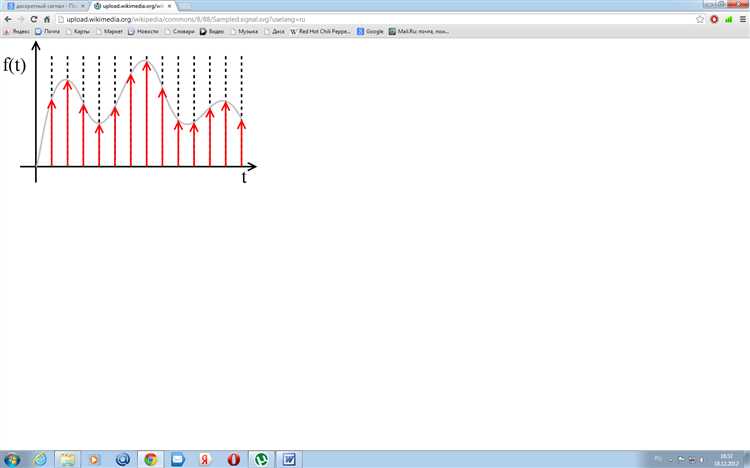
При построении временной шкалы в Mathcad рекомендуется использовать равномерную сетку, что облегчает последующий спектральный анализ и численное преобразование Фурье. Временной диапазон должен покрывать не менее одного периода низкочастотной составляющей для достоверной оценки сигнала.

Частотная шкала формируется из параметров временной дискретизации и длины выборки N. Частотный шаг определяется как Δf = 1/(N·Δt). Для получения разрешения по частоте, необходимого для выделения близких спектральных компонентов, увеличивают N или уменьшают Δt. При этом важно учитывать объём вычислений и ограничения памяти.

В Mathcad для анализа спектра после дискретизации применяют дискретное преобразование Фурье (ДПФ) с использованием временной шкалы, настроенной под требуемый частотный диапазон. При необходимости фильтрации частотного спектра временная сетка корректируется с учётом частотных ограничений сигнала.

Для реализации этих принципов в Mathcad целесообразно задавать временную шкалу как вектор с шагом Δt, а частотную шкалу формировать из результата ДПФ, учитывая сдвиг и симметрию спектра. Это обеспечивает точное сопоставление временных и частотных характеристик сигнала.

Методы интерполяции после дискретизации в Mathcad

В Mathcad для восстановления непрерывного сигнала из дискретных значений применяются несколько ключевых методов интерполяции, позволяющих повысить точность и качество аппроксимации.

1. Линейная интерполяция

   Самый простой способ, при котором значения между узлами рассчитываются как линейные комбинации соседних точек. В Mathcad реализуется через функцию interp с параметром linear. Подходит для сигналов с небольшими изменениями между отсчетами.

2. Полиномиальная интерполяция

   Использует многочлены высокой степени для аппроксимации. Mathcad позволяет задавать степень полинома вручную. Следует избегать слишком высокой степени, чтобы не получить эффект Рунге (перегибы). Рекомендуется для гладких сигналов с низкой частотной составляющей.

3. Сплайновая интерполяция

   Наиболее точный и устойчивый метод, реализованный в Mathcad через функцию splines. Использует кусочно-полиномиальные функции третьей степени (кубические сплайны), обеспечивая непрерывность первой и второй производных. Рекомендуется для большинства практических задач по восстановлению сигналов.

4. Интерполяция с помощью тригонометрических функций

   Метод, основанный на разложении в ряд Фурье. В Mathcad реализуется через функции обработки спектра. Эффективен при работе с периодическими и гармоническими сигналами, где важна частотная точность.

Для выбора оптимального метода в Mathcad учитывайте характер сигнала и требуемую гладкость интерполяции. Линейная подойдет для простых задач и быстрой оценки. Сплайны обеспечивают баланс между точностью и вычислительной нагрузкой. Высокополиномиальная интерполяция требует осторожности из-за возможных артефактов.

Практическая рекомендация: используйте interp с параметром linear для первичной оценки, затем переходите к splines для окончательной аппроксимации и анализа.

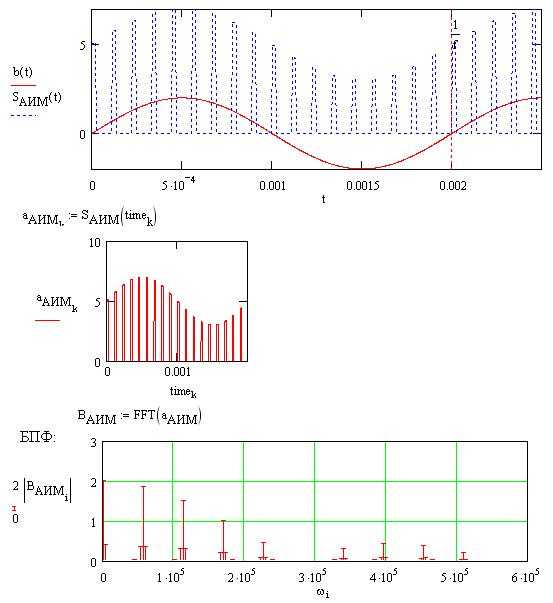
Преобразование дискретных данных для анализа Фурье

Для эффективного анализа спектральных характеристик сигнала в Mathcad применяется дискретное преобразование Фурье (ДПФ). Перед его выполнением важно обеспечить корректную подготовку входных данных.

Исходные дискретные значения должны быть равномерно отсчитаны с постоянным шагом Δt. Несоблюдение равномерности приводит к искажению спектра и появлению артефактов. В Mathcad используется функция fft(), которая требует вектор входных данных длиной, являющейся степенью двойки, что обеспечивает максимальную производительность алгоритма быстрого преобразования Фурье (БПФ).

Если исходный набор данных не соответствует этому требованию, применяются методы дополнения нулями (zero padding) до ближайшей степени двойки. Это увеличивает разрешение спектра без добавления новой информации, улучшая интерпретируемость результатов.

Для снижения эффекта утечки спектра перед применением fft() желательно выполнить оконное преобразование. В Mathcad реализуются окна Ханна, Хэмминга и Блэкмана, которые уменьшают влияние краевых дискретов и сглаживают спектр.

Результат fft() в Mathcad – комплексный вектор, где амплитуда каждого элемента соответствует величине гармоники, а аргумент – её фазе. Для получения спектра амплитуд вычисляется модуль комплексных чисел. Частоты элементов спектра рассчитываются по формуле f = k/(N·Δt), где k – индекс гармоники, N – длина сигнала.

При анализе следует учитывать симметрию спектра для вещественных сигналов: полезна только первая половина результата, остальная содержит комплексно-сопряжённые значения. Выделение этой части упрощает визуализацию и интерпретацию спектра.

Автоматизация дискретизации с помощью скриптов и шаблонов

В Mathcad дискретизация сигналов часто повторяется с одинаковыми параметрами, что делает ручной ввод данных трудоемким. Автоматизация позволяет ускорить процесс и повысить точность расчетов.

Основные шаги для автоматизации дискретизации:

1. Создание скрипта для вычисления выборок по заданному алгоритму дискретизации. Например, можно использовать встроенный язык программирования Mathcad для написания функций, которые принимают параметры частоты дискретизации и длительности сигнала.
2. Определение шаблонов с заранее заданными параметрами дискретизации. Шаблоны позволяют быстро применять стандартные настройки без повторного ввода данных.
3. Интеграция скриптов и шаблонов в основной документ Mathcad для автоматического обновления данных при изменении исходных параметров.

Рекомендации при создании скриптов:

• Используйте массивы и векторы для хранения дискретных значений сигнала, чтобы упростить последующую обработку и визуализацию.
• Применяйте циклы и условия для реализации сложных методов дискретизации, например, адаптивного изменения шага.
• Для повышения универсальности скриптов, параметризуйте все ключевые величины (частота дискретизации, амплитуда, длительность) и реализуйте их передачу через аргументы функций.

Шаблоны можно сохранять как отдельные файлы Mathcad с готовыми модулями дискретизации и подключать к разным проектам. Это ускоряет работу и снижает вероятность ошибок при ручном вводе.

Автоматизация дискретизации с помощью скриптов и шаблонов в Mathcad обеспечивает:

• Стабильность результатов за счет стандартизации расчетных процедур;
• Снижение времени подготовки расчетов;
• Легкость масштабирования и модификации процессов дискретизации.

Вопрос-ответ:

Какие основные методы дискретизации сигналов рассматриваются в Mathcad?

В Mathcad обычно применяются несколько методов дискретизации, среди которых равномерная и неравномерная выборка значений сигнала. Равномерная дискретизация подразумевает фиксированный шаг между точками, что удобно для последующей обработки и анализа. Неравномерная выборка используется, если сигнал меняется с разной скоростью, и позволяет повысить точность в важных участках. Кроме того, в Mathcad можно реализовать методы дискретизации с использованием интерполяции и аппроксимации, что помогает сгладить или реконструировать сигнал после выборки.

Как влияет размер шага дискретизации на качество представления сигнала в Mathcad?

Размер шага дискретизации напрямую влияет на точность и детализацию сигнала. Меньший шаг позволяет получить более точное приближение исходного непрерывного сигнала, поскольку фиксируется больше точек, отражающих его изменения. Однако при очень малом шаге увеличивается объем данных и нагрузка на вычисления. При слишком большом шаге информация теряется, что может привести к искажению или неправильной интерпретации сигнала. В Mathcad рекомендуется выбирать шаг, исходя из частоты изменения сигнала, чтобы избежать эффекта наложения частот (aliasing).

Какие функции Mathcad используются для построения дискретных сигналов и их графического отображения?

Для создания дискретных сигналов в Mathcad применяются функции, которые задают массивы точек с определенным шагом, например, с помощью оператора диапазона или функций типа seq(). Для графического отображения используется встроенный инструмент построения графиков, который позволяет вывести точки в виде дискретной последовательности. Также можно настроить параметры графика — тип точек, линии между ними, цвет и масштаб — для более удобного анализа. При необходимости возможно использовать интерполяционные функции, чтобы визуализировать плавный переход между дискретными точками.

Какие ошибки могут возникать при дискретизации сигналов в Mathcad, и как их избежать?

Основные ошибки связаны с неправильным выбором шага дискретизации и интервалов выборки. Если шаг слишком велик, возникает эффект наложения частот, при котором высокочастотные компоненты сигнала искажаются или теряются. Также при прерывистом или нерегулярном выборе точек возможно появление артефактов на графике. Чтобы избежать таких проблем, нужно анализировать спектр сигнала и подбирать шаг, который не менее чем вдвое превышает максимальную частоту. В Mathcad это можно проверить с помощью встроенных функций анализа, а также визуально контролировать корректность графиков.

Как реализовать адаптивную дискретизацию сигнала в Mathcad?

Адаптивная дискретизация предполагает изменение шага выборки в зависимости от характеристик сигнала, например, его скорости изменения. В Mathcad можно создать алгоритм, который анализирует производную сигнала и в местах с резкими изменениями уменьшает шаг дискретизации, а в более спокойных участках — увеличивает. Для этого обычно применяют циклы и условные операторы, создавая массивы точек с переменным шагом. Такой подход позволяет получить более точное представление сигнала без излишнего увеличения объема данных.