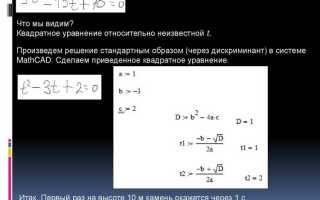
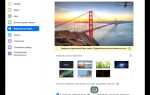
Mathcad позволяет решать системы линейных и нелинейных уравнений с помощью встроенных функций и символьных вычислений. Чтобы задать систему уравнений, необходимо использовать операторы определения (:=), а не равенства. Каждое уравнение записывается как выражение, приравненное к нулю. Например, f1(x, y) := x + y — 5.
Для численного решения применяется функция find. Перед её использованием нужно задать вектор неизвестных: vars := [x, y], и начальные приближения: guess := [1, 1]. Затем вызывается find(vars), где vars – список переменных, а приближения задаются непосредственно выше вызова.
Если требуется аналитическое решение, используется функция solve в символьном режиме. Например: solve(x + y = 5, x — y = 1). Для этого уравнения записываются с использованием знака равенства, а затем выделяются и преобразуются через символическую панель (Ctrl + .).
При решении нелинейных систем следует использовать осмысленные приближения, так как функция find может не сойтись при плохом выборе начальных значений. Mathcad не отображает пошаговый процесс, поэтому рекомендуется проверять систему визуализацией графиков или промежуточных расчетов.
Подготовка переменных и задание уравнений в Mathcad
Перед решением системы уравнений необходимо явно определить все переменные. В Mathcad это делается с помощью оператора присваивания :=. Например, для задания начальных значений переменных x и y используйте записи вида: x := 0, y := 1.
Убедитесь, что единицы измерения указаны корректно, если расчёты связаны с физическими величинами. Mathcad автоматически отслеживает размерности, и ошибка в единицах может привести к некорректному решению или невозможности вычислений.
Задание уравнений осуществляется с использованием символа равенства =, а не оператора присваивания. Например: x + y = 3. Уравнения не должны содержать неопределённых переменных. Если в уравнении присутствует переменная, которой не присвоено значение или не задано выражение, Mathcad выдаст ошибку.
Для ввода системы уравнений используйте локальную область (Given Block). Она начинается с ключевого слова Given, за которым следует список уравнений. Например:
Given
x + y = 5
2·x — y = 1
После этого необходимо указать, какие переменные требуется найти. Это делается с помощью функции find, например: find(x, y). Результатом будет численное решение системы.
Не используйте в одной области определения и вызовы функций, использующих эти же переменные, чтобы избежать конфликтов. Все переменные, используемые в уравнениях, должны быть локальными или явно переопределены перед блоком Given.
Выбор метода решения: символьный или численный подход
В Mathcad доступны два основных подхода к решению систем уравнений – символьный и численный. Выбор зависит от типа системы, целей анализа и необходимости точного выражения решения.
- Символьный метод используется через оператор
solve,или функцииsolve(),find()в символьном режиме. Он позволяет получить аналитическое выражение переменных. Эффективен при небольшом количестве уравнений с алгебраической структурой, например: -
eq1 := x + y = 10 eq2 := x - y = 2 solve(eq1, eq2, x, y)
- Рекомендуется, если нужно проверить зависимость решений от параметров или использовать результат в дальнейшем упрощении.
- Недостаток – невозможность решения систем с трансцендентными функциями или уравнениями, не имеющими аналитического решения.
- Численный метод применяется через функцию
find()вне символьного контекста. Обязательно задать начальные приближения: -
x := 1; y := 1 eq1 := x + sin(y) = 2 eq2 := x^2 + y = 5 find(x, y)
- Подходит для сложных нелинейных систем, включая тригонометрические, экспоненциальные и логарифмические зависимости.
- Важно: при плохом выборе начальных значений решение может не сойтись или найти локальный корень.
Практически: сначала пробуют символьное решение – оно дает полное представление. Если не удается или система сложная – переходят к численному. При использовании численного метода полезно визуализировать уравнения или провести анализ чувствительности к начальному приближению.
Использование функции solve для нахождения неизвестных

В Mathcad функция solve применяется для поиска значений переменных, удовлетворяющих заданной системе уравнений. Основное требование – система должна быть записана в символьной форме, а не через операторы := и =.
Для корректного применения необходимо задать уравнения через символическое равенство ≡ (обычно вызывается комбинацией клавиш Ctrl + =). Все выражения должны быть подготовлены заранее, без присваивания значений переменным. Например:
eq1: x + y ≡ 5
eq2: x — y ≡ 1
После определения уравнений вызывается функция:
solve(eq1, eq2, x, y)
Функция возвращает символьное выражение с найденными значениями. Чтобы получить численные значения, используется обертка float:
float(solve(eq1, eq2, x, y))
Для систем с тремя и более переменными подход остаётся тем же. Количество уравнений должно соответствовать количеству неизвестных, иначе результат будет неопределён.
Если решения не существует, Mathcad отобразит сообщение об ошибке. В этом случае рекомендуется проверить уравнения на совместность или использовать функцию find для численного поиска.
Применение блока Given-Find для систем с несколькими переменными
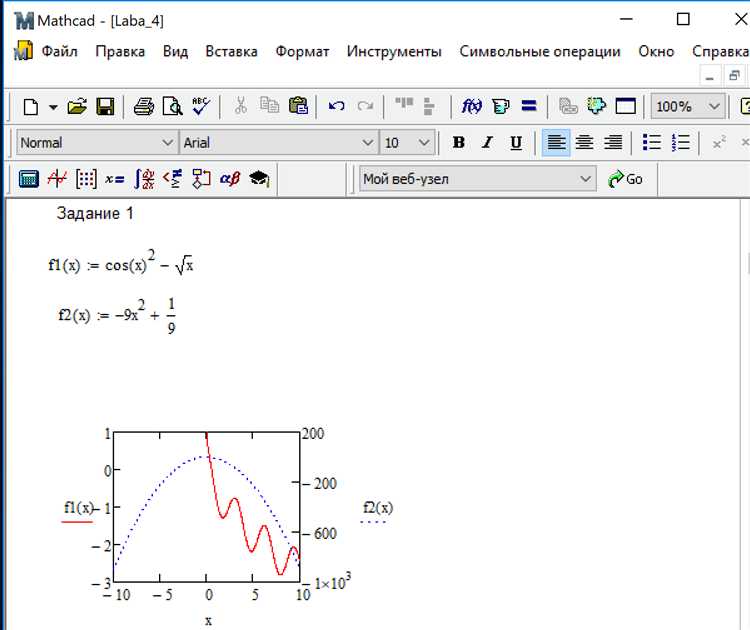
Для решения системы нелинейных или линейных уравнений с несколькими переменными в Mathcad используется блок Given-Find, обеспечивающий структурированное задание условий и автоматический подбор значений переменных.
Внутри блока Given перечисляются уравнения системы, каждое из которых вводится отдельно, без необходимости вручную преобразовывать выражения. Уравнения могут быть как алгебраическими, так и включать встроенные функции, производные, тригонометрические выражения.
После всех уравнений вызывается функция Find(переменная1, переменная2, …), где в скобках указываются все неизвестные. Mathcad решает систему численно, основываясь на начальных приближениях, которые необходимо задать до блока Given:
x := 1 y := 1 z := 1 Given x + y + z = 6 x - y + 2*z = 4 2*x + y - z = 3 Find(x, y, z)
Для корректного решения необходимо задать начальные приближения для каждой переменной. Без них Mathcad не сможет применить численные методы. Выбор начальных значений влияет на скорость сходимости и вероятность нахождения корректного решения.
Функция Find возвращает вектор значений переменных, соответствующий решению системы. Результат можно напрямую присвоить новой переменной:
R := Find(x, y, z)
Для доступа к отдельным элементам решения используйте индексацию:
R[0 → x R[1 → y R[2 → z
Система может содержать любое количество переменных и уравнений, при этом число уравнений должно совпадать с числом переменных. В противном случае Mathcad выдаст ошибку несовместности. Блок Given-Find не поддерживает символьное решение – используется исключительно численный метод Ньютона или модифицированные итерационные алгоритмы.
Настройка начальных приближений и ограничений для численного решения

В Mathcad при решении систем нелинейных уравнений методами численного анализа важна корректная постановка начальных приближений. Без них итерационные алгоритмы могут не сойтись или дать неверные корни.
Начальные приближения задаются в виде векторов или отдельных значений переменных, близких к предполагаемым решениям. В Mathcad для функций find и Given можно указать начальные значения через параметр «guess». Рекомендуется выбирать приближения, основанные на аналитическом анализе, графиках или предыдущих вычислениях.
Чем ближе начальное приближение к реальному решению, тем быстрее сойдется метод и выше вероятность нахождения нужного корня. Для сложных систем желательно проверять несколько начальных точек, чтобы избежать попадания в локальные экстремумы.
Ограничения переменных можно задать через логические условия в блоках Given или использовать функции с областью определения. Mathcad позволяет добавлять неравенства или условия вида x ≥ a, y ≤ b. Они критичны, если физический смысл задачи исключает часть области решения или требуется обеспечить устойчивость вычислений.
Включение ограничений повышает надежность результата и предотвращает выход итераций за пределы допустимых значений, что особенно важно при использовании методов Ньютона и модифицированных алгоритмов.
Для контроля процесса решения рекомендуется анализировать сходимость и промежуточные значения переменных, изменяя начальные приближения и ограничения, если алгоритм не стабилен или результаты несопоставимы с ожидаемыми.
Проверка полученных решений и анализ результатов
После решения системы уравнений в Mathcad необходимо провести точную проверку корректности и адекватности полученных корней. Без этого этапа невозможно гарантировать правильность расчетов и избежать ошибок в дальнейших вычислениях.
- Подстановка результатов в исходные уравнения:
- Подставьте каждое найденное значение переменной обратно в исходные уравнения.
- Проверьте, что левая и правая части уравнений совпадают с точностью, заданной настройками Mathcad.
- Если расхождение превышает установленный порог (обычно 10-6 или меньше), необходимо перепроверить шаги решения.
- Анализ физического смысла и ограничений:
- Оцените, соответствуют ли корни реалистичным условиям задачи (например, отрицательные значения для длины или массы недопустимы).
- Проверьте область допустимых значений переменных, заданную в Mathcad, и исключите неподходящие решения.
- Сравнение с альтернативными методами:
- Решите систему численно другим способом – например, методом Ньютона или итерациями.
- Сопоставьте результаты для выявления стабильности и устойчивости решения.
- Использование функции проверки ошибок Mathcad:
- Активируйте встроенный механизм оценки точности и ошибок.
- Обратите внимание на предупреждения о приближениях и сходимости.
- Анализ чувствительности:
- Измените исходные параметры системы в небольшом диапазоне.
- Отследите влияние изменений на полученные решения, чтобы выявить устойчивость модели.
Такая системная проверка позволяет не только подтвердить правильность вычислений, но и обеспечить надежность интерпретации результатов в контексте задачи.
Отображение и оформление решений с помощью встроенных инструментов Mathcad
Для комплексных систем рекомендуется визуализировать результаты с помощью встроенных графиков. Mathcad поддерживает построение двух- и трехмерных графиков, что позволяет анализировать зависимость решений от параметров. При настройке графиков нужно обязательно указывать оси, легенды и заголовки, чтобы избежать двусмысленности в интерпретации данных.
Дополнительно можно использовать встроенные блоки комментариев и аннотаций, которые помогают пояснять ход решения и выделять ключевые этапы вычислений. В итоговой презентации решения полезно оформлять результаты в виде списка с использованием маркеров или нумерации, чтобы улучшить восприятие и структурировать информацию.
Вопрос-ответ:
Как задать систему уравнений в Mathcad для решения?
Для начала необходимо ввести каждое уравнение системы с использованием переменных. Убедитесь, что все уравнения записаны в правильной форме, например, с помощью знака равенства. Затем переменные должны быть объявлены, если требуется, и система подготавливается к решению с помощью встроенных функций, таких как `solve` или `Given`. Важно точно указать все уравнения, чтобы Mathcad корректно их распознал.
Каким образом можно решить систему уравнений в Mathcad по шагам?
Для пошагового решения сначала определяют переменные, затем вводят уравнения. После этого применяют функцию решения, например, `Given` для обозначения условий, а затем вызывают функцию `Find` для поиска значения переменных. При этом можно использовать промежуточные вычисления для контроля результатов. Такой подход позволяет проследить логику решения и увидеть, как изменяются значения переменных на каждом этапе.
Как поступить, если система уравнений не имеет явного аналитического решения в Mathcad?
Если аналитический способ не подходит, используют численные методы. Mathcad позволяет применять функции численного решения, например, `root` или `Find`, которые ищут корни уравнений методом приближений. Важно правильно задать начальные приближения для переменных, чтобы алгоритм сходился. Такой подход помогает найти решения для сложных систем, где точное выражение невозможно получить.
Можно ли решить систему уравнений с параметрами и получить общий вид решения?
Да, Mathcad позволяет работать с системами, содержащими параметры. Для этого переменные параметров задают как символические, а сами уравнения оставляют в общем виде. После этого с помощью функций символьной математики можно получить выражения решений через эти параметры. Однако в некоторых случаях Mathcad может ограничиваться численными решениями, если выражения слишком сложные.