Для нахождения максимума функции в Mathcad используется встроенная функция maximize. Она принимает в качестве аргументов определённую функцию и переменную, по которой осуществляется оптимизация. В отличие от аналитических методов, Mathcad выполняет численную оптимизацию, что позволяет находить экстремумы даже для сложных, неявных или кусочных функций.
Перед использованием maximize, необходимо задать начальное приближение, которое оказывает существенное влияние на результат. Если функция имеет несколько локальных максимумов, Mathcad вернёт значение, соответствующее ближайшему из них. Поэтому рекомендуется предварительно построить график функции и определить участки, где может находиться глобальный максимум.
Формат вызова функции: maximize(f(x), x = x₀), где f(x) – функция, x – переменная, x₀ – начальное приближение. Если переменная входит в функцию в нескольких местах или участвует в условиях, важно явно задать все зависимости. Для более точных результатов можно использовать дополнительные параметры: шаг оптимизации, границы области поиска и точность вычислений через панель параметров Mathcad.
Mathcad также поддерживает оптимизацию при наличии ограничений. В этом случае применяются функции maximize совместно с constraints. Условия вводятся через операторы неравенств, а сам поиск осуществляется численно, с учётом всех заданных ограничений. Такой подход эффективен в инженерных задачах, где параметры функции должны удовлетворять физическим или техническим требованиям.
Настройка области определения функции для поиска максимума
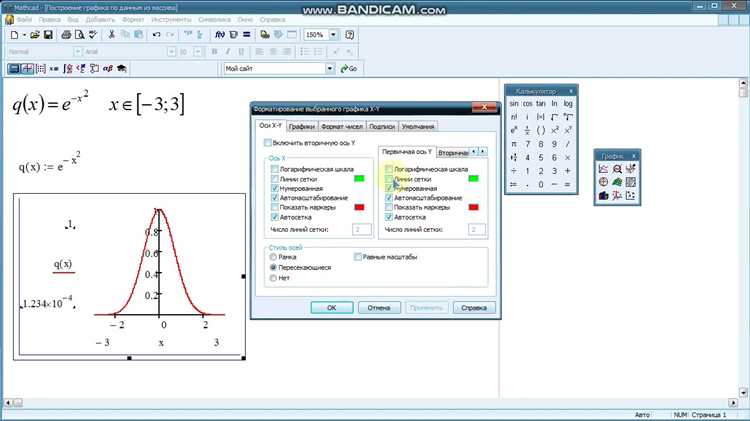
Перед использованием встроенной функции maximize в Mathcad, необходимо строго задать область определения переменной, по которой производится оптимизация. Без точного указания границ вычисления невозможны или дают некорректные результаты.
- Область определения задается с помощью оператора диапазона:
x := a, b..c, гдеa– начальное значение,c– конечное,b– шаг (опционально). - Если шаг не указан, Mathcad определяет его автоматически, что может привести к пропуску экстремумов. Рекомендуется явно задавать шаг, особенно при исследовании функций с несколькими локальными максимумами.
- Границы должны соответствовать области допустимых значений функции. Например, для функции
ln(x)не следует включать ноль или отрицательные значения.
При работе с функциями нескольких переменных:
- Используйте векторные диапазоны:
x := a..b,y := c..d. - Функцию
maximizeприменяйте к определению переменной вектором, например:maximize(f, x_vector). - Для сложных ограничений применяйте условные операторы внутри определения функции, например:
f(x) := if x > 0 then выражение else NaN.
Избегайте слишком широких диапазонов: это увеличивает время вычислений и снижает точность. Оптимально начинать с предварительного анализа графика функции для определения локальных участков, в которых может находиться максимум.
Использование встроенной функции maximize
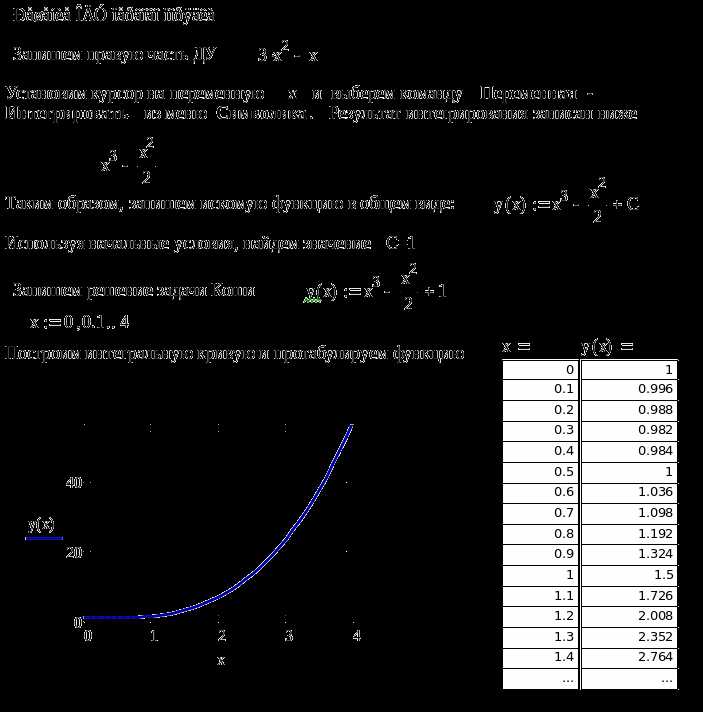
Функция maximize(f(x), x) в Mathcad применяется для численного поиска максимума функции одной переменной. Она возвращает значение переменной x, при котором функция f(x) достигает локального максимума. Чтобы результат был корректным, необходимо обеспечить выполнение ряда условий.
- Перед вызовом
maximizeнеобходимо определить функциюf(x)явно. Например:f(x) := -x² + 4x + 1. - Переменная
xдолжна иметь начальное приближение. Указывается до вызоваmaximize, например:x := 0. - Результат зависит от начального значения:
maximizeнаходит локальный максимум, ближайший к заданной начальной точке. - Функция должна быть непрерывной в окрестности предполагаемого максимума. Разрывы или неограниченный рост приводят к ошибкам вычислений.
- Для ограничения области поиска используйте конструкцию
maximize(f(x), x = a..b), гдеaиb– границы интервала.
Рекомендации по использованию:
- Перед применением
maximizeпостроить график функции, чтобы визуально оценить количество экстремумов и выбрать разумное начальное приближение. - Если функция имеет несколько максимумов, запустить
maximizeс разными начальными значениями для выявления всех возможных решений. - Проверять результат подстановкой: сравнить
f(x)в найденной точке с соседними значениями. - Для гладких функций предпочтительно использовать символьное определение, если это возможно, с последующим численным уточнением.
Поиск максимума графически через вставку графика
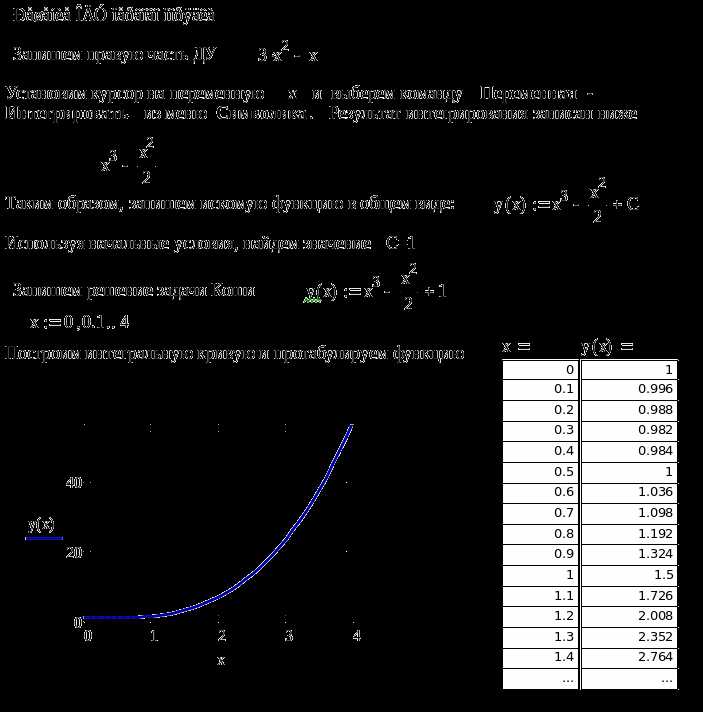
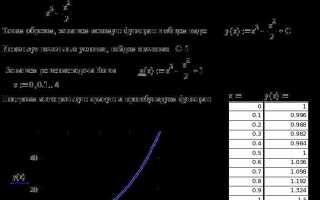
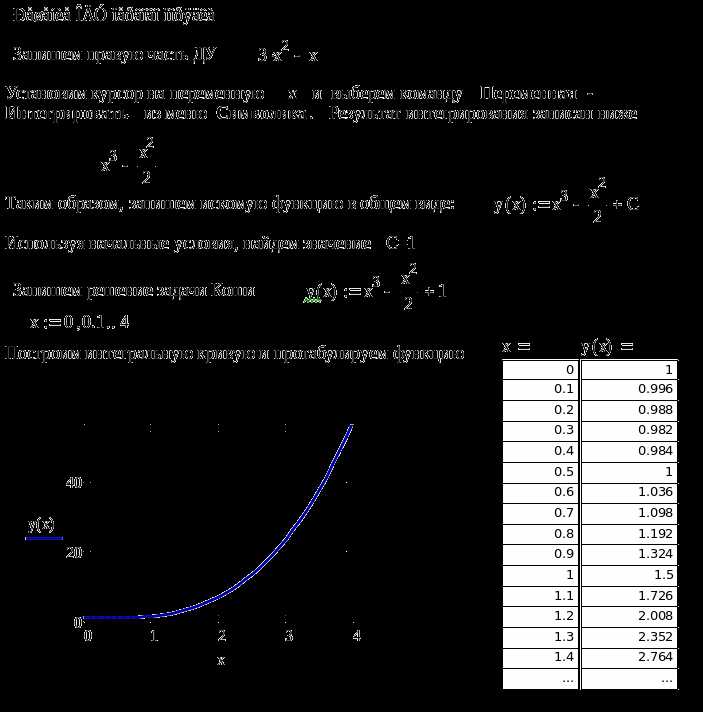
В Mathcad поиск максимума функции можно выполнить визуально, используя график. Для этого необходимо определить функцию и построить её на подходящем интервале значений аргумента.
Например, пусть задана функция f(x) := -x² + 4x + 1. Введите её в рабочей области и задайте интервал: x := 0, 0.1..5. Это создаст вектор значений аргумента с шагом 0.1.
Вставьте график через панель Вставка → График → X-Y график. На ось X перетащите переменную x, на ось Y – f(x). График отобразит параболу. Вершина параболы соответствует максимуму функции на заданном интервале.
Чтобы точно определить координаты максимума, используйте инструмент курсора на графике. Наведите указатель на вершину и считайте значения по осям. Также можно временно увеличить масштаб выбранного участка с помощью рамки мышью для более точной оценки координат максимума.
Графический метод полезен, когда аналитическое выражение слишком громоздкое или содержит параметры, влияющие на форму кривой. Он позволяет оперативно оценить поведение функции и определить максимальные значения без применения численных методов.
Указание начального приближения и его влияние на результат
В Mathcad для поиска максимума функции с помощью численных методов, таких как maximize или minimize, необходимо задать начальное приближение. Это значение критически влияет на точность и успешность нахождения глобального экстремума.
Если функция имеет несколько локальных экстремумов, выбор начального приближения определяет, к какому из них сойдётся алгоритм. Например, при анализе функции f(x) = x·sin(x) в интервале [0, 10], установка начального приближения x₀ = 2 приведёт к поиску максимума вблизи x ≈ 2, тогда как x₀ = 7 – к другому локальному максимуму. Без учёта поведения функции в заданной области возможно получить некорректный результат.
Для повышения надёжности результата рекомендуется предварительно построить график функции, визуально определить участки с потенциальными максимумами и выполнять несколько запусков с разными начальными значениями. В случае сложных функций – использовать производные или анализ второй производной для оценки поведения вблизи начальной точки.
Рекомендация: задавайте начальное приближение осознанно, исходя из анализа графика и особенностей функции. Не полагайтесь на случайный выбор значений, особенно в задачах с высокой чувствительностью к локальным изменениям.
Решение задач поиска максимума с ограничениями
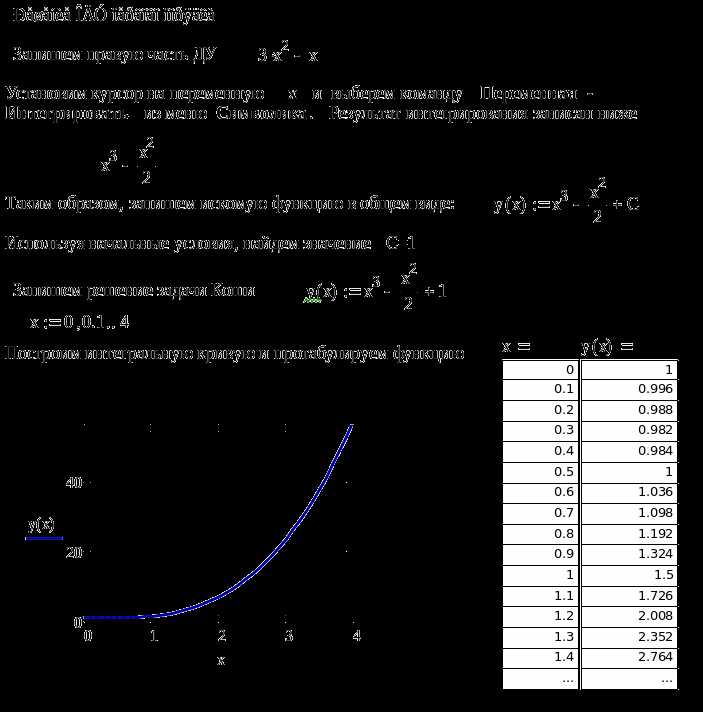
В Mathcad для нахождения максимума функции при наличии ограничений используется встроенная функция maximize совместно с системой уравнений или неравенств, определяющей допустимую область. Перед применением maximize необходимо сформировать выражение целевой функции и задать ограничения в виде логических условий.
Пример: требуется найти максимум функции f(x, y) = x·y при ограничениях x + y ≤ 10, x ≥ 2, y ≥ 1. В Mathcad создаются уравнения ограничений с использованием оператора given, а затем вызывается maximize(f(x, y), x, y) после определения всех условий.
Все переменные должны быть предварительно заданы в разумных пределах, иначе Mathcad не сможет выполнить оптимизацию. Рекомендуется использовать начальные приближения с помощью команды guess value, особенно при нескольких переменных.
Для неравенств используется логическая запись: x + y ≤ 10 вводится как x + y <= 10. Все ограничения должны быть перечислены после given и до вызова maximize.
При наличии сложных ограничений (например, нелинейных) желательно проверить выполнимость условий отдельно, используя функцию Find для тестирования допустимого решения. Это позволяет избежать ошибок оптимизации из-за пустой области поиска.
Если функция имеет несколько локальных максимумов, Mathcad может найти только один из них, зависящий от начального приближения. В таких случаях рекомендуется варьировать начальные значения и анализировать полученные результаты.
Обработка ошибок при неудачном поиске максимума
В Mathcad функция maximize может возвращать ошибку, если не удаётся определить максимум в заданной области. Частая причина – отсутствие начального приближения или его выбор вне области допустимых значений. Для устранения ошибки необходимо проверить область определения функции и выбрать начальное значение, находящееся внутри неё.
Если функция содержит разрывы или не определена в некоторых точках, Mathcad может не завершить оптимизацию. Для диагностики используйте график функции перед применением maximize. Визуализация позволяет выявить резкие скачки, асимптоты или недопустимые области.
Неправильная структура самой функции – ещё один источник ошибок. Убедитесь, что в выражении нет деления на переменные, которые могут принимать ноль, и что не используются логарифмы от отрицательных чисел. Используйте встроенные условия ограничения вида if, чтобы исключить такие ситуации.
Если Mathcad сообщает об ошибке “No solution found”, проверьте параметры: шаг, допустимую погрешность и границы. Иногда слишком узкие или широкие границы мешают сходимости. Изменение этих параметров через TOL и диапазоны переменной может привести к успешному поиску максимума.
Также важно удостовериться, что сама функция пригодна для оптимизации. Не все выражения имеют максимум в заданной области. Если функция монотонна или имеет экстремум на границе, maximize может не дать ожидаемый результат. В таких случаях используйте ручной анализ или визуальный поиск экстремума.
Сравнение нескольких методов поиска максимума в Mathcad
Mathcad предлагает несколько подходов к поиску максимума функции: оператор maximize, визуальный анализ графика, численное моделирование через блок solve и использование встроенных функций оптимизации. Каждый из методов имеет свои особенности и применим в зависимости от задачи.
Оператор maximize предназначен для численного поиска максимума при наличии начального приближения. Он применим только к скалярным функциям одной переменной. Для многомерных функций необходимо использовать блок solve с неравенствами и системой условий.
Визуальный анализ графика дает представление о возможных точках максимума, но не обеспечивает точных координат. Метод удобен для предварительной оценки, особенно при сложных или разрывных функциях, где аналитический анализ невозможен.
Блок solve позволяет формализовать условия экстремума через производные и ограничения. Метод требует явного задания уравнений и подходит для задач с ограничениями. Производные можно задавать вручную или с использованием встроенной функции diff.
Функция genfit и подобные методы на основе минимизации невязки часто применяются для поиска параметров модели с максимальным соответствием данным. Хотя это косвенный способ, он эффективен в задачах регрессии и аппроксимации.
Сравнение методов:
| Метод | Преимущества | Ограничения |
|---|---|---|
| maximize | Простота, высокая скорость | Ограничен одной переменной, требует начального приближения |
| Графический анализ | Интуитивная наглядность | Нет численной точности, ограничен визуальным восприятием |
| solve с производными | Поддержка ограничений, гибкость | Сложность формализации, необходимость задания всех условий |
| Оптимизация модели | Подходит для реальных данных | Косвенность метода, требуется корректная модель |
Для гладких функций без ограничений рекомендуется maximize. В задачах с условиями и несколькими переменными эффективен solve. При анализе экспериментальных данных предпочтительны методы на основе подгонки.