
При работе с матрицами в Mathcad часто возникает необходимость вычисления вспомогательной (побочной) диагонали. Эта задача особенно актуальна при анализе симметричных или диагонально доминирующих матриц, а также при реализации алгоритмов, использующих элементы этой диагонали как опорные значения.
В Mathcad нет встроенной функции для прямого извлечения вспомогательной диагонали, но её можно получить с помощью индексации элементов. Если матрица имеет размер n × n, элементы вспомогательной диагонали можно получить с помощью выражения: M[i, n — 1 — i], где i изменяется от 0 до n — 1. Это выражение следует ввести в цикл или использовать с векторной индексацией для получения всех элементов сразу.
Для автоматизации вычислений рекомендуется создать вектор индексов i := 0..n-1 и затем использовать выражение diag := M[i, n — 1 — i]. Mathcad корректно обработает это выражение при условии, что размерность матрицы M задана заранее, а переменная n соответствует её размеру. Такая реализация удобна для встраивания в более сложные вычислительные модули и облегчает повторное использование кода.
Результат вычисления можно напрямую визуализировать или использовать для дальнейших операций, таких как проверка на симметрию, построение условных зависимостей или оценка устойчивости численных алгоритмов. Mathcad обеспечивает точность и наглядность при работе с такими выражениями, особенно в инженерных расчётах.
Определение понятий: основная и вспомогательная диагонали
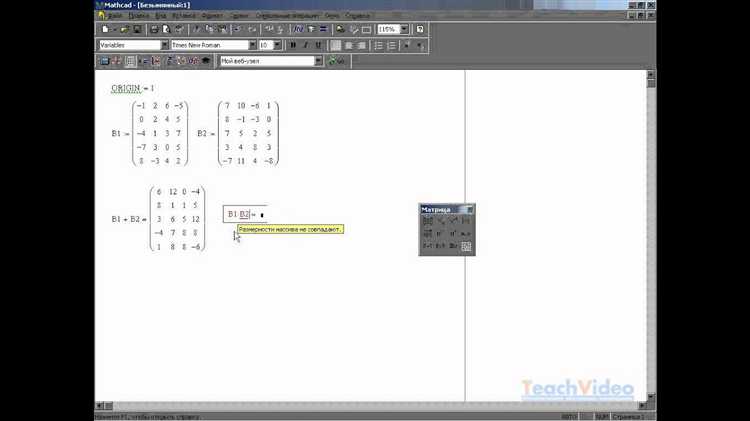
В квадратной матрице размером n×n различают две диагонали: основную и вспомогательную. Их точное понимание необходимо для корректной работы с элементами массива в среде Mathcad.
- Основная диагональ – это множество элементов, расположенных от левого верхнего угла до правого нижнего. Формально: элемент Ai,i, где i = 0, 1, …, n−1.
- Вспомогательная диагональ – противоположная диагональ, проходящая от правого верхнего угла к левому нижнему. Индексация: Ai,n−1−i, где i = 0, 1, …, n−1.
В Mathcad индексация массивов начинается с нуля. Это важно учитывать при извлечении элементов диагоналей. Ошибки часто возникают при использовании неправильных индексов для вспомогательной диагонали.
Рекомендации для корректной работы:
- Убедитесь, что матрица квадратная: число строк равно числу столбцов.
- Для основной диагонали используйте равные индексы строк и столбцов: A[i, i].
- Для вспомогательной диагонали применяйте формулу: A[i, n−1−i], где n – размер матрицы.
- Проверяйте границы массива, особенно при работе с переменными размерностями.
Формирование матрицы исходных данных в Mathcad
Для создания матрицы исходных данных в Mathcad необходимо задать размерность и заполнить элементы по индексам. Матрица вводится с помощью оператора :=, после чего указывается имя и структура. Например, A := ⎡1 2 3⎤ ⎢4 5 6⎥ ⎣7 8 9⎦ формирует матрицу 3×3.
Индексация в Mathcad начинается с нуля. Это следует учесть при последующих вычислениях, особенно при обращении к элементам по индексам. Если требуется изменить начальный индекс, можно использовать переменную ORIGIN := 1, но рекомендуется оставлять ORIGIN = 0 для корректной работы встроенных функций.
Для генерации больших матриц рационально использовать вложенные циклы или функцию stack. Например, использование выражения stack(v₀, v₁, v₂) объединит векторы-строки в единую матрицу. Векторы можно формировать с помощью диапазонов: v := 1, 2 .. 10 создаст одномерный массив от 1 до 10 с шагом 1.
Численные значения могут быть заданы вручную либо вычислены по формуле. Для программно заданных матриц удобно использовать функции, возвращающие элементы по формулам: A(i, j) := i + 2·j, где i и j – индексы строк и столбцов соответственно. Далее применить genmat(A, m, n) для генерации матрицы размером m×n.
Важно контролировать единообразие размерностей при построении матриц через выражения и функции. Несоответствие длины векторов приведёт к ошибкам компиляции. Для проверки используйте встроенную функцию rows(A) и cols(A), определяющие количество строк и столбцов соответственно.
Использование индексов для обращения к элементам диагонали
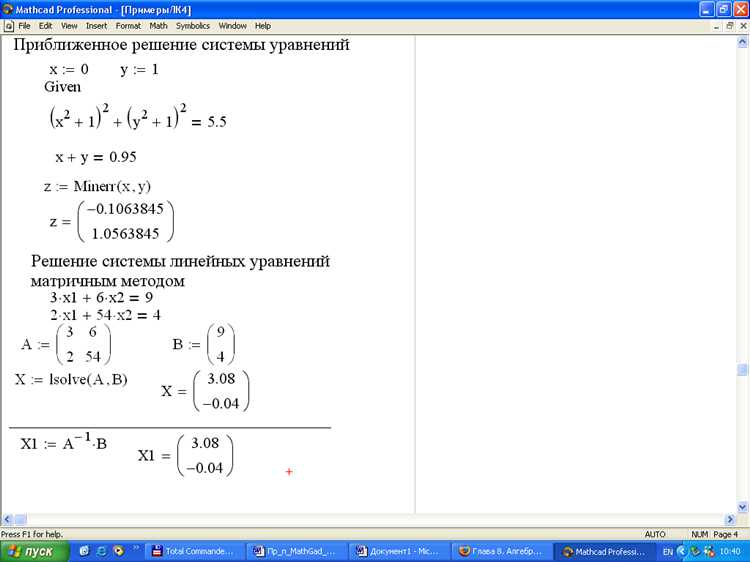
В Mathcad индексация матриц начинается с нуля, что критично при работе с диагоналями. Вспомогательная диагональ матрицы определяется как набор элементов, расположенных от верхнего правого до нижнего левого угла. Для квадратной матрицы размером N×N элементы вспомогательной диагонали имеют индексы вида A[i, N−1−i], где i ∈ [0, N−1].
При реализации выборки элементов диагонали следует использовать цикл с переменной i, изменяющейся от 0 до N−1. Каждый элемент диагонали вычисляется выражением A[i, N−1−i]. Для извлечения всех значений диагонали удобно создать вектор D размерности N, где D[i := A[i, N−1−i]].
Mathcad требует явного задания размерности переменных. Перед выполнением операций необходимо определить размерность исходной матрицы с помощью функции rows(A), возвращающей количество строк. Это значение используется для определения границ цикла.
При обращении к диагональным элементам важно контролировать корректность индексов, особенно при работе с подматрицами или матрицами, полученными из пользовательского ввода. Любое нарушение диапазона приведёт к ошибке исполнения.
В случае изменения размера матрицы следует обновить соответствующие границы индексации, чтобы избежать обращения к несуществующим элементам. Использование индексов вида A[i, N−1−i] даёт максимальную гибкость при работе с диагоналями различной длины и обеспечивает точный доступ к каждому элементу вспомогательной диагонали.
Пошаговое извлечение вспомогательной диагонали из квадратной матрицы

В Mathcad вспомогательная (побочная) диагональ квадратной матрицы проходит от верхнего правого угла к нижнему левому. Для извлечения элементов этой диагонали используется индексная адресация с учетом размеров матрицы.
1. Определите квадратную матрицу A размером n×n. Например:
A := ⎡1 2 3⎤
⎢4 5 6⎥
⎣7 8 9⎦
2. Узнайте индекс последнего столбца: n — 1. В Mathcad индексация начинается с нуля.
3. Создайте вектор индексов i от 0 до n — 1:
i := 0..n-1
4. Извлеките элементы вспомогательной диагонали с помощью выражения:
diag := Ai, n — 1 — i
5. В результате вы получите вектор элементов вспомогательной диагонали. Для приведенной выше матрицы A результат будет:
diag = ⎡3, 5, 7⎤
6. Для автоматизации оберните выражение в функцию:
auxDiag(A) := Ai, cols(A) — 1 — i
7. Функция корректно работает только с квадратными матрицами. Добавьте проверку: if rows(A) ≠ cols(A), возвращайте ошибку или null-вектор.
Построение функции для нахождения вспомогательной диагонали
Для нахождения вспомогательной диагонали в Mathcad необходимо определить координаты вершин фигуры и задать соответствующую функцию. Допустим, фигура представляет собой четырёхугольник с вершинами A, B, C, D, заданными в виде векторов: A := [x₁, y₁], B := [x₂, y₂], C := [x₃, y₃], D := [x₄, y₄]. Вспомогательной диагональю будем считать отрезок, соединяющий несмежные вершины, например, AC или BD.
Создайте функцию расстояния между двумя точками:
dist(u, v) := sqrt((u[0 — v[0])² + (u[1 — v[1])²)
Для построения диагонали AC вызовите:
diag := dist(A, C)
Если диагональ определяется по пересечению прямых, например, AD и BC, необходимо найти их уравнения. Определите направляющие векторы:
v₁ := D — A
v₂ := C — B
Найдите параметры пересечения с помощью системы:
solve(A + t·v₁ = B + s·v₂, [t, s])
Решив её, подставьте найденное значение t или s в соответствующее уравнение прямой, чтобы получить координаты точки пересечения – она будет серединой вспомогательной диагонали при симметрии.
Для автоматизации оформите процесс в виде вложенной функции, возвращающей длину, координаты или уравнение диагонали в зависимости от параметров. Обеспечьте контроль ввода координат, проверку коллинеарности и исключите вырожденные случаи.
Автоматизация расчёта диагонали при изменении размеров матрицы

Чтобы не пересчитывать вручную при каждом изменении размера n, необходимо задать n как переменную, от которой зависят размеры массива. Далее создаётся массив индексов от 0 до n−1 с помощью функции range, например: i := 0..n−1.
Затем вспомогательная диагональ формируется через векторное обращение к элементам матрицы:
diag_aux := A[i, n−1−i
Эта запись обеспечивает автоматическое обновление всех значений при изменении n или элементов матрицы A. Все вычисления адаптируются к новым условиям без дополнительного редактирования формул.
Важно, чтобы матрица оставалась квадратной. Для контроля используйте проверку rows(A) = cols(A). При необходимости добавьте условие прекращения вычислений или выдачи ошибки в случае несоответствия.
Автоматизация диагонального расчёта особенно эффективна при работе с параметрически определяемыми матрицами, например:
A := stack(seq(i + j, j, 0, n−1), i, 0, n−1)
Это обеспечивает создание матрицы заданного размера без необходимости ручного ввода значений, сохраняя корректность диагональных вычислений.
Для извлечения вспомогательной диагонали матрицы в Mathcad необходимо использовать индексный доступ и операции над векторами. Предположим, дана квадратная матрица A размером n×n. Вспомогательной считается диагональ, идущая из правого верхнего угла в левый нижний, то есть элементы A[i, n-1-i], где i – индекс строки.
- Определите размер матрицы:
n := rows(A). - Создайте вектор индексов:
i := 0 .. n - 1. - Вычислите вспомогательную диагональ:
diag := A[i, n - 1 - i].
Результат – вектор diag, содержащий элементы вспомогательной диагонали в порядке от верхнего правого угла к нижнему левому.
- Для работы с не квадратными матрицами используйте
min(rows(A), cols(A))для определения длины диагонали. - Если необходимо инвертировать порядок элементов – примените функцию
reverse(diag). - Для последующей обработки или визуализации используйте функции
stackилиplotс индексированной подстановкой.
Визуализация диагонали на графике средствами Mathcad
Для отображения вспомогательной диагонали на графике в Mathcad используйте функцию plot из блока Graph. Начните с задания координатных точек диагонали в виде двух векторов: x и y. Например, если диагональ проводится от точки (x₁, y₁) до (x₂, y₂), определите:
x := [x₁, x₂]
y := [y₁, y₂]
Откройте панель построения 2D-графиков и выберите компонент X-Y Plot. Перетащите его в рабочую область. Введите x по оси X и y по оси Y. Диагональ будет отображена как отрезок между двумя заданными точками.
Для визуального выделения используйте параметры графика. Щёлкните по линии и настройте цвет, толщину и стиль линии. Например, выберите красный цвет и пунктирную линию для подчёркивания вспомогательной роли диагонали.
Если график содержит другие элементы (например, прямоугольник или фигуру, внутри которой строится диагональ), добавьте соответствующие функции в тот же компонент X-Y Plot. Для этого определите контур фигуры отдельными векторами и добавьте их к графику в виде дополнительных кривых.
Для автоматической корректировки масштаба используйте команду Autoscale в контекстном меню графика. Это обеспечит видимость всей диагонали вне зависимости от её положения и длины.
Чтобы сделать подписи к началу и концу диагонали, создайте вектора с текстовыми метками с помощью функции text box и вручную разместите их вблизи соответствующих точек.
Результат – чётко визуализированная диагональ, встроенная в график, с возможностью точной настройки внешнего вида для отчётности или анализа.
Вопрос-ответ:
Как в Mathcad задать матрицу, чтобы затем найти вспомогательную диагональ?
Для начала нужно ввести квадратную матрицу. Это делается через вкладку «Массив» — выберите нужное количество строк и столбцов, затем заполните элементы. После ввода матрицы можно обратиться к ее элементам, используя двойную индексацию. Вспомогательная диагональ — это элементы, расположенные от правого верхнего угла к левому нижнему. Для матрицы A размером N×N она определяется выражением A[i, N−i−1], где i меняется от 0 до N−1.
Какая формула используется для нахождения вспомогательной диагонали?
В Mathcad можно использовать цикл или векторизацию. Формула для элементов вспомогательной диагонали выглядит так: `A[i, n − i − 1]`, где `n` — размерность матрицы, а `i` — индекс строки. Это выражение выбирает элементы, лежащие на диагонали, идущей из правого верхнего в левый нижний угол. Если оформить это через вектор, то можно создать диапазон `i := 0..n−1`, а затем сформировать вектор `diag := A[i, n−i−1]`.
Можно ли обойтись без циклов при выделении вспомогательной диагонали в Mathcad?
Да, можно. Mathcad поддерживает векторные операции, и при правильной постановке задачи циклы часто не требуются. Если определить диапазон индексов, а затем обратиться к элементам матрицы с помощью индексирования массивов, Mathcad автоматически создаст вектор значений диагонали. Такой способ не только короче, но и делает выражения более наглядными.
Что делать, если матрица не квадратная?
Вспомогательная диагональ определена только для квадратных матриц. Если матрица прямоугольная, то её диагонали не определяются однозначно — либо не существует полной вспомогательной диагонали, либо она состоит не из n элементов. Чтобы решить задачу, матрицу нужно привести к квадратному виду — либо использовать подматрицу, либо пересчитать размерность, если это допустимо с точки зрения задачи.
Почему элементы вспомогательной диагонали нумеруются именно так — A[i, n−i−1]?
Нумерация в Mathcad начинается с нуля. Поэтому верхний правый элемент квадратной матрицы с размерностью n будет иметь индекс [0, n−1], а нижний левый — [n−1, 0]. Чтобы пройти по всем элементам этой диагонали, при каждом увеличении строки на единицу необходимо уменьшать номер столбца на единицу. Это и реализуется в выражении A[i, n−i−1], где `i` — индекс строки, а `n−i−1` — соответствующий индекс столбца.






