Обратная матрица – ключевой элемент в решении систем линейных уравнений и анализе линейных преобразований. Maple предлагает встроенные функции для вычисления обратной матрицы, что значительно ускоряет работу по сравнению с ручными методами.
Для быстрого получения обратной матрицы достаточно воспользоваться функцией MatrixInverse() из стандартной библиотеки Maple. Она принимает матрицу в виде объекта Matrix и возвращает ее обратную при условии, что определитель не равен нулю.
Чтобы минимизировать время вычислений, рекомендуется сначала проверить определитель через Determinant(). Если определитель равен нулю, попытка найти обратную матрицу приведет к ошибке. Также важно использовать тип данных Dense Matrix для ускорения операций, особенно при работе с большими матрицами.
Подготовка матрицы к вычислению обратной в Maple
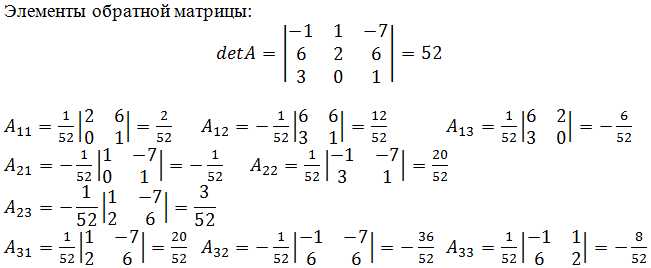
Для корректного нахождения обратной матрицы в Maple необходимо сначала создать матрицу в правильном формате. В Maple используется команда Matrix() из пакета LinearAlgebra. Матрица должна быть квадратной, иначе обратная не существует.
Перед вычислением обратной проверьте определитель матрицы командой Determinant(A), где A – ваша матрица. Если определитель равен нулю, обратная матрица отсутствует, и дальнейшие вычисления будут невозможны.
При вводе элементов матрицы рекомендуется использовать точные значения (дроби или целые числа) вместо десятичных приближений, чтобы избежать ошибок при вычислениях.
Если матрица задана как список списков, конвертируйте её в объект Matrix с помощью A := Matrix([[a11, a12], [a21, a22]]);. Для больших матриц оптимально задавать элементы программно или импортировать из файлов в форматах CSV или TXT с последующим преобразованием.
После подготовки и проверки матрицы её можно передать в функцию Inverse(A) для вычисления обратной. Рекомендуется использовать оператор with(LinearAlgebra): в начале сессии для удобства вызова функций.
Команда для нахождения обратной матрицы: inv()

В Maple функция inv() используется для вычисления обратной матрицы. Аргументом команды должна быть квадратная матрица, заданная в виде объекта типа Matrix.
Пример создания матрицы и вычисления обратной:
A := Matrix([[1, 2], [3, 4]]);
inv(A);
Команда inv(A) возвращает новую матрицу, которая является обратной к A, если она существует. В противном случае Maple выдаст ошибку или предупреждение, указывающее на необратимость матрицы.
Для ускорения работы с большими матрицами рекомендуется проверить определитель с помощью LinearAlgebra[Determinant](A). Если он равен нулю, обратной матрицы не существует, и вызов inv() бессмысленен.
При вычислении обратной матрицы для матриц с числовыми элементами Maple выполняет операции точно, используя рациональные числа, что повышает точность по сравнению с вычислениями в плавающей точке.
Для применения inv() внутри выражений можно использовать сокращённую форму A^(-1), которая эквивалентна вызову inv(A).
Проверка существования обратной матрицы с помощью Maple
Обратная матрица существует только для невырожденных матриц, то есть с ненулевым определителем. В Maple определить, можно ли найти обратную, достаточно просто – нужно вычислить детерминант.
Для матрицы A команда вычисления детерминанта выглядит так: Determinant(A);. Если результат равен нулю, обратной матрицы не существует. При отличном от нуля значении можно переходить к вычислению обратной матрицы.
Для автоматизации проверки можно использовать условный оператор, например:
if Determinant(A) <> 0 then Inverse(A) else "Обратная матрица не существует" end if;
Эта конструкция позволяет избежать ошибок при попытке инвертировать вырожденную матрицу и сразу получить информативный результат.
Если матрица большая и вычисление детерминанта занимает время, можно проверить ранг матрицы командой Rank(A);. Если ранг совпадает с размерностью матрицы, обратная существует.
Таким образом, в Maple для проверки обратимости матрицы достаточно вычислить детерминант или ранг, что обеспечивает быстрый и точный результат без лишних вычислений.
Обработка ошибок при вычислении обратной матрицы в Maple

В Maple для вычисления обратной матрицы используется функция MatrixInverse(A) или оператор A^(-1). Основная ошибка при работе с этими командами возникает, если матрица вырождена (необратима). В этом случае Maple выдаст сообщение об ошибке или вернёт выражение с параметром, указывающим на невозможность вычисления.
Чтобы предотвратить сбой программы, перед вызовом обратной матрицы рекомендуется проверить определитель матрицы с помощью Determinant(A). Если результат равен нулю, матрица необратима, и дальнейшие вычисления не имеют смысла.
Для автоматической обработки ошибок можно использовать конструкцию try ... catch ... end try, например:
try
invA := MatrixInverse(A);
catch
print(«Ошибка: матрица необратима или вычисление невозможно»);
end try;
Это позволяет избежать прерывания скрипта и вывести информативное сообщение. Альтернативно, можно использовать условие:
if Determinant(A) <> 0 then
invA := MatrixInverse(A);
else
print("Матрица необратима");
end if;
В случае работы с числовыми матрицами важно учитывать влияние ошибок округления. Если определитель близок к нулю, но не равен ему, стоит проверить условие числа с помощью evalf(Determinant(A)) с заданной точностью. При малых значениях можно либо увеличить точность вычислений, либо использовать метод регуляризации, например, добавив к диагонали небольшое значение (Tikhonov regularization).
Оптимизация размера и типа матрицы перед инверсией

В Maple скорость вычисления обратной матрицы напрямую зависит от её размера и структуры. Перед вызовом функции MatrixInverse важно исключить избыточные строки и столбцы. Для этого используйте команды LinearAlgebra:-RowReduce или LinearAlgebra:-PivotedMatrix – они помогают выявить и убрать линейно зависимые компоненты.
Обращайте внимание на тип матрицы: если она разреженная, применяйте функцию SparseMatrix. Это существенно сокращает время вычислений и потребление памяти. Для плотных матриц используйте тип Matrix, но избегайте преобразований с избыточными типами данных (например, не переводите целочисленные матрицы в числовые с плавающей точкой без необходимости).
Перед инверсией рекомендуется проверить определитель через LinearAlgebra:-Determinant. Если определитель близок к нулю, стоит применить регуляризацию или уменьшить размер матрицы за счёт удаления малоинформативных строк и столбцов.
Используйте подматрицы или блоки, если матрица блочно-разделима. Функции ExtractMatrix и BlockMatrix позволяют выделить меньшие части, инвертировать их отдельно и затем собрать итоговую обратную матрицу. Это уменьшает вычислительную нагрузку и повышает устойчивость результата.
Оптимизация типа и размера матрицы перед инверсией в Maple повышает эффективность алгоритмов, снижая время и ресурсы без потери точности.
Использование пакетов Maple для работы с матрицами
Для эффективной работы с матрицами в Maple рекомендуется использовать специализированные пакеты, предоставляющие расширенные функции и оптимизированные алгоритмы.
- LinearAlgebra – базовый пакет для работы с линейной алгеброй. Включает функции для вычисления обратной матрицы, определителя, ранга и др.
- linalg – устаревший пакет, заменённый на LinearAlgebra, но в некоторых версиях Maple поддерживается для совместимости.
- MatrixTools – дополнительный набор функций для работы с большими матрицами, полезен при работе с разреженными или блочными матрицами.
Для быстрого нахождения обратной матрицы в пакете LinearAlgebra используется функция Inverse(). Перед вызовом функции необходимо подключить пакет:
with(LinearAlgebra):
Inverse(A);где A – квадратная матрица. Функция автоматически проверяет невырожденность матрицы и выдаёт ошибку, если обратная матрица не существует.
При работе с большими матрицами полезно использовать функции, позволяющие предварительно проверить свойства матрицы:
Determinant(A);– вычисление определителя, чтобы убедиться, что он не равен нулю.Rank(A);– определение ранга для проверки полноты ранга.IsInvertible(A);– быстрый булевский тест на обратимость (доступен в некоторых версиях).
Для оптимизации вычислений с разреженными матрицами следует использовать пакет SparseMatrixTools, который снижает нагрузку на память и ускоряет операции.
Включение и использование пакетов происходит командой with(ИмяПакета):. Чтобы избежать засорения пространства имён, рекомендуется использовать команду в начале рабочей сессии.
Экспорт и сохранение обратной матрицы из Maple
После вычисления обратной матрицы в Maple важно сохранить результат для дальнейшего использования или передачи. Maple поддерживает несколько форматов экспорта, подходящих для различных целей.
- Сохранение в переменную:
Чтобы сохранить обратную матрицу в переменную, используйте присвоение:
invA := LinearAlgebra[MatrixInverse](A);Это упростит повторное использование без повторного вычисления.
- Экспорт в текстовый файл (например, CSV):
Maple позволяет сохранить матрицу в формате CSV для работы в других программах:
ExportMatrix := (M, filename) -> FileTools[Text][Export](filename, MatrixToList(M, 'list')):Пример вызова:
ExportMatrix(invA, "inverse_matrix.csv");Этот метод обеспечивает простую загрузку данных в Excel, Python и др.
- Экспорт в Maple-файл (*.mpl):
Для сохранения вычислений в собственном формате Maple используйте команду:
save invA "inverse_matrix.mpl";Позволяет впоследствии загружать переменную командой
read "inverse_matrix.mpl": - Экспорт в LaTeX:
Если требуется включить матрицу в научный документ, Maple генерирует LaTeX-код:
latex(invA);Результат можно скопировать и вставить в текст редактора с поддержкой LaTeX.
Рекомендуется перед экспортом проверить размер и формат матрицы, чтобы избежать ошибок при импорте в другие программы. Для больших матриц предпочтителен CSV, для научных публикаций – LaTeX.
Практические примеры нахождения обратной матрицы в Maple

Для быстрого вычисления обратной матрицы в Maple используется встроенная функция MatrixInverse. Рассмотрим конкретный пример: зададим матрицу
A := Matrix([[2, 1, 3], [0, 1, 4], [5, 2, 0]]);
Для получения обратной матрицы достаточно выполнить команду:
invA := MatrixInverse(A);
Maple сразу вернёт точное выражение для обратной матрицы. Если требуется численное приближение, используйте функцию evalf:
evalf(invA);
Для проверки корректности вычисления умножьте исходную матрицу на найденную обратную:
simplify(A . invA);
Результатом будет единичная матрица, что подтверждает правильность решения.
Если матрица имеет параметрический вид, например:
B := Matrix([[a, b], [c, d]]);
функция MatrixInverse(B); вернёт обратную матрицу в символическом виде, выраженную через параметры a, b, c, d, при условии, что определитель не равен нулю.
В случае больших разреженных матриц удобно использовать пакет LinearAlgebra[Sparse], который оптимизирует вычисления и экономит ресурсы.
Пример для разреженной матрицы:
with(LinearAlgebra[Dense]):
S := SparseMatrix(3, 3, [1, 3, 2], [2, 1, 3], [4, 5, 6]);
invS := MatrixInverse(S);
Таким образом, для эффективного и точного нахождения обратных матриц в Maple используйте MatrixInverse с последующей проверкой через умножение на исходную матрицу.
Вопрос-ответ:
Как в Maple быстро найти обратную матрицу для квадратной матрицы?
В Maple для вычисления обратной матрицы можно использовать встроенную функцию `MatrixInverse` из пакета LinearAlgebra. Сначала нужно загрузить пакет командой `with(LinearAlgebra):`, затем применить функцию к нужной матрице, например: `MatrixInverse(A)`. Это самый простой способ получить обратную матрицу, если исходная матрица невырожденная.
Что делать, если в Maple при попытке найти обратную матрицу появляется ошибка или сообщение о необратимости?
Ошибка при вычислении обратной матрицы часто возникает, если матрица является вырожденной, то есть её определитель равен нулю. Для проверки перед вычислением нужно найти определитель: `Determinant(A)`. Если результат равен нулю, обратной матрицы не существует. В таком случае стоит проверить исходные данные или использовать псевдообратную, например с помощью функции `MoorePenroseInverse`.
Можно ли в Maple найти обратную матрицу для матрицы с параметрами или символическими выражениями?
Да, Maple позволяет работать с матрицами, содержащими символы и параметры. Для таких матриц также применяется `MatrixInverse`, но результат будет выражением в терминах параметров. При этом важно учитывать, что обратная матрица существует только при условии, что определитель не обращается в ноль при заданных параметрах. Для проверки можно использовать условие `assume` или анализировать определитель отдельно.
Как оптимизировать вычисление обратной матрицы в Maple для больших матриц?
Для больших матриц лучше избегать прямого вычисления обратной, так как это может быть ресурсоёмко. В Maple можно использовать разложение LU с последующим решением систем уравнений, что быстрее и точнее. Также можно воспользоваться функцией `LinearSolve`, которая позволяет решить систему без явного вычисления обратной матрицы. Такой подход снижает нагрузку и уменьшает время вычислений.