Как в maple решить уравнение

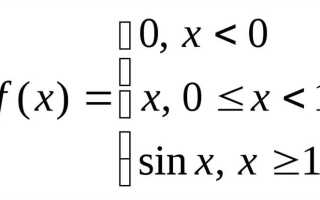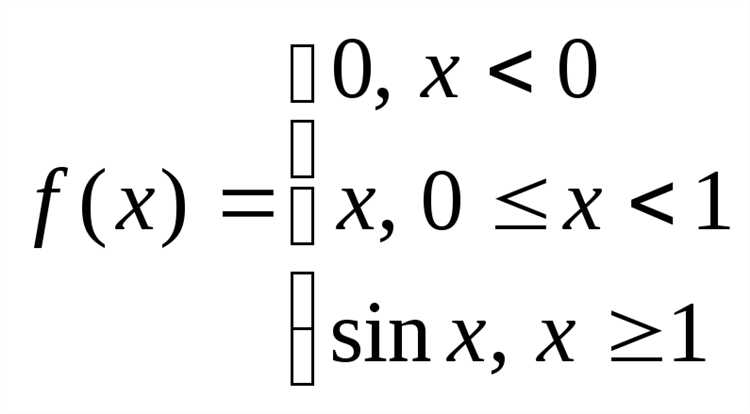
Maple – мощная среда для символических вычислений, которая позволяет решать уравнения всех типов: алгебраические, дифференциальные, трансцендентные. В отличие от обычных калькуляторов, Maple не просто вычисляет корни, но предоставляет подробные аналитические выражения, сохраняет параметры и позволяет управлять точностью решения.

Чтобы решить алгебраическое уравнение в Maple, используется команда solve. Например, команда solve(x^2 — 4 = 0, x) вернёт два точных корня: x = -2 и x = 2. При этом можно указывать переменные явно, если уравнение содержит несколько переменных. Maple также поддерживает решение систем уравнений: solve({x + y = 3, x — y = 1}, {x, y}).

Для численного решения применяется команда fsolve. Она особенно полезна при наличии трансцендентных уравнений, таких как sin(x) = x/2. Команда fsolve(sin(x) = x/2, x) вернёт приближённое значение корня. При необходимости можно указать интервал: fsolve(sin(x) = x/2, x = 0 .. 2), чтобы получить конкретный корень в заданной области.

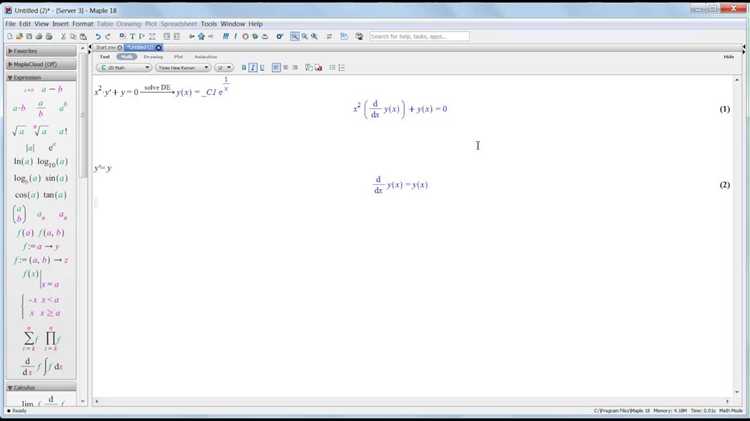
Решение дифференциальных уравнений осуществляется с помощью dsolve. Например, dsolve(diff(y(x), x) = y(x), y(x)) возвращает общее решение y(x) = _C1*exp(x). Для получения частного решения необходимо задать начальные условия: dsolve({diff(y(x), x) = y(x), y(0) = 1}, y(x)).

Maple позволяет работать и с параметрическими уравнениями, предоставляя аналитические выражения для корней в зависимости от параметров. Это делает его особенно удобным для математического моделирования и инженерных задач, где важна не только численная точность, но и структура решения.

Как решить линейное уравнение с одной переменной в Maple

Для решения линейного уравнения вида ax + b = 0 в Maple используется команда solve. Эта функция возвращает точное аналитическое значение переменной.

Пример: решим уравнение 3*x — 7 = 2.

Введите команду:

solve(3*x — 7 = 2, x);

Результат: x = 3. Maple автоматически выражает переменную x и упрощает результат.

Если необходимо сохранить результат в переменную, используйте:

sol := solve(3*x — 7 = 2, x);

Чтобы проверить решение, выполните подстановку с помощью команды subs:

subs(x = sol, 3*x — 7);

Ожидаемый результат: 2, что подтверждает правильность решения.

Уравнение можно вводить в любом алгебраическом виде. Maple автоматически упрощает выражения и приводит их к стандартной форме. Для символа умножения всегда используйте *.

Если коэффициенты содержат параметры, Maple вернёт решение в общем виде. Например:

solve(a*x + b = 0, x);

Результат: x = -b/a, при условии a ≠ 0.

Решение системы линейных уравнений с использованием команды solve

В Maple система линейных уравнений решается при помощи команды solve, принимающей список уравнений и переменных. Пример:

eq1 := 2*x + 3*y = 7:
eq2 := 4*x - y = 1:
solve({eq1, eq2}, {x, y});

Команда возвращает точное аналитическое решение. В данном примере результатом будет:

{x = 1, y = 1}

Рекомендации при использовании:

• Использовать фигурные скобки { } для задания системы уравнений – порядок не имеет значения.
• Все уравнения и переменные должны быть явно заданы. Пропуск переменной приведёт к решению в общем виде.
• Если переменных больше, чем уравнений, Maple вернёт общее решение с параметрами.
• Для вещественных решений добавить параметр RealDomain: solve({eq1, eq2}, {x, y}, RealDomain).

Для систем с большим числом уравнений рекомендуется предварительно упрощать выражения через simplify или collect, чтобы повысить читаемость и производительность.

Если необходимо получить численное приближение, использовать evalf:

evalf(solve({2*x + 3*y = 7, 4*x - y = 1}, {x, y}));

Для получения решения в виде списка уравнений, используйте опцию explicit=true:

solve({eq1, eq2}, {x, y}, explicit=true);

При работе с параметрическими системами используйте solve совместно с assume для задания условий на параметры:

assume(a::real, b::real):
solve({a*x + b*y = 1, x - y = 0}, {x, y});

Работа с квадратными уравнениями: извлечение корней и проверка

Для решения квадратного уравнения в Maple используется команда solve. Например, уравнение x^2 - 5*x + 6 = 0 решается так:

solve(x^2 - 5*x + 6 = 0, x);

Результат: 2, 3 – это корни уравнения. Maple возвращает их в явном виде, даже если они комплексные или иррациональные. Для работы с дискриминантом используйте discrim:

discrim(x^2 - 4*x + 1, x);

Результат: 12 – положительный дискриминант, следовательно, два действительных корня.

Для извлечения корней в символьной форме можно использовать solve без явных чисел, например:

solve(a*x^2 + b*x + c = 0, x);

Ответ будет содержать выражение с sqrt(b^2 - 4*a*c), что полезно для анализа параметров.

Проверка корней выполняется подстановкой в исходное уравнение с использованием subs и simplify:

simplify(subs(x=2, x^2 - 5*x + 6));

Если результат 0, корень верен. Аналогично проверяется второй корень.

Для численного уточнения решений используйте evalf:

evalf(solve(x^2 + x + 1 = 0, x));

Ответ: -0.5 + 0.8660254038*I, -0.5 - 0.8660254038*I – комплексные корни с десятичной точностью.

Чтобы явно указать, что уравнение имеет комплексные корни, примените isolve – он вернёт пустое множество, что подтверждает отсутствие целых решений:

isolve(x^2 + 1 = 0);

Как задать и решить параметрическое уравнение

В Maple параметрические уравнения задаются с использованием переменных и параметров, отличных от основной переменной. Для задания используйте оператор solve или fsolve в зависимости от типа решения (точного или численного). Параметры обозначаются обычными символами, и Maple рассматривает их как константы до явного указания.

Пример. Задать уравнение с параметром a:

eq := a*x^2 + 3*x - 1 = 0;
solve(eq, x);

Maple вернёт общее решение через a. Для получения решения при конкретном значении параметра:

subs(a = 2, eq);
solve(%, x);

Если требуется исследовать, при каких значениях параметра уравнение имеет действительные корни, используйте дискриминант:

disc := discriminant(lhs(eq), x);
solve(disc >= 0, a);

Для численного решения с конкретным параметром используйте:

fsolve(subs(a = -1.5, eq), x);

Системы параметрических уравнений задаются аналогично. Пример:

sys := [a*x + y = 1, x - a*y = 2];
solve(sys, {x, y});

Maple вернёт решение через параметр a. Чтобы определить, при каких a система имеет единственное решение, используйте определитель коэффициентов:

A := Matrix([[a, 1], [1, -a]]);
LinearAlgebra:-Determinant(A);
solve(%, a);

При значениях a, при которых определитель не равен нулю, система имеет единственное решение. Чтобы избежать неопределённостей, рекомендуется всегда проверять особые случаи с помощью assume или case analysis.

Применение команды fsolve для численного решения уравнений

Команда fsolve в Maple используется для численного решения нелинейных уравнений и систем. В отличие от solve, она возвращает приближённые значения корней с плавающей точкой. Это особенно полезно, когда аналитическое решение отсутствует или слишком громоздкое.

Синтаксис: fsolve(уравнение, переменная). Например, чтобы найти корень уравнения sin(x) = x/2, используйте fsolve(sin(x) = x/2, x). Результат – приближённое значение корня, например, fsolve вернёт 0.0, если корень близок к нулю.

Для уточнения диапазона поиска можно задать интервал: fsolve(sin(x) = x/2, x = -5 .. 5). Это ограничит область анализа и ускорит вычисления, особенно при наличии нескольких корней. При отсутствии корней в указанном интервале fsolve не вернёт результат.

Для систем уравнений используется формат: fsolve({уравнение1, уравнение2}, {переменная1, переменная2}). Пример: fsolve({x^2 + y^2 = 1, x = y}, {x, y}) даст одно из численных решений системы.

Если требуется повысить точность результата, используйте Digits: Digits := 20: перед вызовом fsolve. Это полезно в задачах, чувствительных к ошибкам округления.

Команда не гарантирует нахождение всех корней. Чтобы найти несколько решений, рекомендуется выполнять многократные вызовы fsolve с разными интервалами. Также следует учитывать, что fsolve работает только с уравнениями, содержащими вещественные корни – комплексные решения она не находит.

Решение уравнений с комплексными переменными

Для решения уравнений с комплексными переменными в Maple используется стандартная команда solve, которая учитывает комплексную область значений по умолчанию. Чтобы найти все комплексные корни, необходимо задать переменную как комплексную или явно указать соответствующее условие.

Пример решения уравнения z^2 + 1 = 0, где z – комплексная переменная:

solve(z^2 + 1 = 0, z);

Maple вернет два комплексных корня: z = I и z = -I, где I – мнимая единица. Если требуется работать с комплексными переменными более явно, можно задать переменную через assume:

assume(z, complex);

При решении более сложных уравнений с комплексными переменными рекомендуется использовать fsolve с опцией complex для численного поиска корней. Например, уравнение exp(z) = z:

fsolve(exp(z) = z, z, complex);

В случаях, когда уравнение содержит параметры, которые могут менять количество или тип корней, полезно применять команду allvalues для извлечения всех значений решения:

allvalues(solve(z^3 - 1 = 0, z));

Чтобы проанализировать распределение корней на комплексной плоскости, можно визуализировать найденные значения с помощью plottools[pointplot]. Для систем уравнений с комплексными переменными Maple допускает ввод переменных в виде пар действительной и мнимой части, что расширяет возможности численных методов.

Для уравнений с параметрами и комплексными переменными рекомендуется применять пакет Student[ComplexAnalysis], в котором доступны специализированные функции для комплексных преобразований и поиска корней. Важной практикой является проверка решений подстановкой с помощью eval для исключения посторонних корней.

Как задать систему нелинейных уравнений и найти все решения

В Maple система нелинейных уравнений задаётся списком или набором уравнений, объединённых в фигурные скобки. Для поиска всех решений применяют функцию solve или более мощный fsolve с параметром для множественных корней.

• Объявите переменные, например: vars := {x, y};
• Сформируйте систему, например:
  sys := {x^2 + y^2 = 1, x^3 - y = 0};
• Для точных решений вызовите:
  solve(sys, vars);
  – результат будет в виде списка всех корней, если они существуют в алгебраическом виде.
• Если решений много или аналитическое решение сложно, примените численный метод:
  fsolve(sys, vars, {x = -2 .. 2, y = -2 .. 2});
  – область поиска задаётся явно, чтобы найти все корни внутри заданного диапазона.
• Для систем с несколькими решениями рекомендуется использовать параметр allsolutions = true в fsolve для нахождения всех численных корней:

fsolve(sys, vars, allsolutions = true, {x = -2 .. 2, y = -2 .. 2});

Так Maple переберёт все области поиска и вернёт все корни внутри указанных границ.

• Проверяйте корректность ввода уравнений: каждое уравнение должно быть равенством (=), а не выражением.
• Если переменных много, укажите их все в списке или множестве при вызове solve или fsolve.
• Для повышения точности используйте параметр digits в fsolve.

Пример для поиска всех численных решений в диапазоне:

vars := {x, y};
sys := {x^2 + y^2 = 1, x^3 - y = 0};
fsolve(sys, vars, allsolutions = true, {x = -1.5 .. 1.5, y = -1.5 .. 1.5});

Анализ уравнений с условием: использование опции assuming

В Maple опция assuming позволяет уточнить область определения переменных при решении уравнений, что повышает точность и релевантность результата. Она применяется непосредственно в командах solve и fsolve, ограничивая множество решений заданными условиями.

Например, для уравнения sqrt(x) = 2 без условий Maple выдаст корень x = 4. Если добавить условие x > 0 через assuming, результат останется тем же, но при усложнении уравнения это поможет исключить нежелательные комплексные или отрицательные решения.

Синтаксис выглядит так:

solve(уравнение, переменная) assuming условие;

В условии можно задавать:

– неравенства (x > 0),

– принадлежность к множеству (x::real, y::integer),

– логические связки (x > 0 and y < 5).

Например, решение уравнения x^2 = 4 с ограничением x > 0:

solve(x^2 = 4, x) assuming x > 0;

Результат: x = 2, в отличие от полного решения x = ±2.

Использование assuming эффективно при работе с параметрическими уравнениями и системами, где важно учитывать контекст задачи. Оно исключает из рассмотрения неподходящие решения, ускоряя вычисления и упрощая интерпретацию результатов.

Рекомендуется использовать assuming при решении уравнений с параметрами, если известно ограничение на параметры или переменные, а также при анализе функций с областью определения, отличной от всей числовой оси.

Вопрос-ответ:

Как в Maple решить уравнение первого порядка с одной переменной?

В Maple для решения уравнения первого порядка с одной переменной используют команду `solve`. Например, чтобы найти корни уравнения \(2x + 3 = 7\), нужно написать `solve(2*x + 3 = 7, x);`. Эта команда выдаст значения переменной \(x\), удовлетворяющие уравнению. Если уравнение сложнее, можно использовать дополнительные параметры для уточнения решения.

Можно ли в Maple решать системы нелинейных уравнений? Как это сделать?

Да, Maple умеет работать с системами нелинейных уравнений. Для этого также применяется функция `solve`, но в качестве первого аргумента передаётся список уравнений. Например, чтобы решить систему \(\{x^2 + y^2 = 1, x — y = 0\}\), вводят `solve({x^2 + y^2 = 1, x — y = 0}, {x, y});`. Maple вернёт все пары \((x, y)\), которые удовлетворяют одновременно обоим уравнениям.

Как в Maple найти все корни многочлена с помощью команды solve?

Чтобы получить все корни многочлена, нужно использовать `solve` с указанием переменной. Например, для уравнения \(x^3 — 6x^2 + 11x — 6 = 0\) команда будет `solve(x^3 — 6*x^2 + 11*x — 6 = 0, x);`. Maple выдаст все вещественные и комплексные корни. Если интересуют только вещественные корни, можно дополнительно применить функцию `RealDomain` или ограничить решение с помощью условий.

Можно ли в Maple решать дифференциальные уравнения и какие команды для этого использовать?

В Maple есть инструменты для решения дифференциальных уравнений. Для обыкновенных дифференциальных уравнений используется команда `dsolve`. Например, для уравнения \(\frac{dy}{dx} = y\) вводят `dsolve(diff(y(x), x) = y(x), y(x));`. Maple выдаст общее решение или частное, если заданы начальные условия. Аналогично, для более сложных уравнений `dsolve` позволяет получить аналитические решения.

Как в Maple решить уравнение с параметрами и получить решение в зависимости от параметра?

Если уравнение содержит параметр, Maple позволяет выразить решение через него. Например, для уравнения \(ax + b = 0\) с параметрами \(a\) и \(b\), вводят `solve(a*x + b = 0, x);`. Maple выдаст ответ в виде \(x = -b/a\), где решение зависит от значений параметров. Важно учитывать условия, например, что \(a \neq 0\), чтобы решение имело смысл.