Как в mathcad решить уравнение

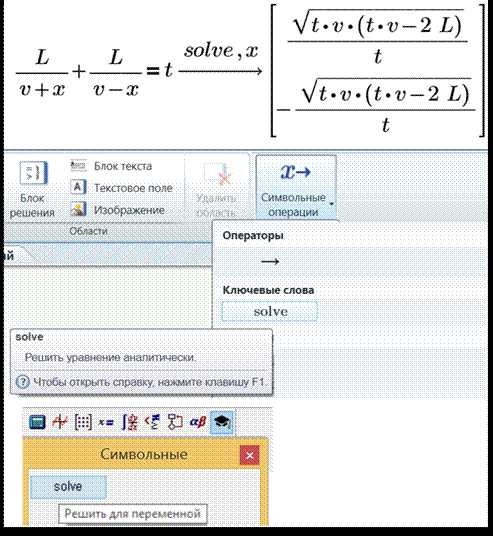
Mathcad предоставляет инструменты для решения алгебраических, дифференциальных и систем уравнений с точностью до заданных параметров. В основе работы лежит ввод уравнения в естественном математическом формате, что ускоряет настройку задачи и минимизирует ошибки.

Первый этап – выбор метода решения. Для нелинейных уравнений применяются встроенные численные алгоритмы, такие как метод Ньютона или секущих, которые запускаются через функцию solve. Для систем уравнений важно задать начальные приближения, чтобы гарантировать сходимость решения.

Вторая ключевая задача – корректная постановка переменных и ограничений. Mathcad позволяет вводить параметры с точностью до машинного эпсилон, что важно при вычислениях с малыми значениями или близкими корнями. Использование оператора given помогает задавать дополнительные условия, влияющие на результат.

Настройка среды Mathcad для работы с уравнениями

Перед началом решения уравнений в Mathcad важно оптимизировать интерфейс и параметры для удобства и точности вычислений. Первым шагом выберите режим документа с необходимой точностью вычислений – рекомендуются настройки с плавающей точкой двойной точности (Double Precision), обеспечивающей погрешность не выше 10^-15.

Перейдите в меню «Формат» → «Настройки» и установите стандартный стиль ввода математических выражений, включающий поддержку встроенных операторов и символов (например, знак корня √, степень и индексы). Для упрощения работы с уравнениями активируйте опцию автоматического распознавания операторов равенства и неравенств.

Настройте отображение числовых результатов через меню «Формат» → «Числовые форматы» с выбором фиксированного или экспоненциального формата, в зависимости от требуемого диапазона значений. Установите количество отображаемых десятичных знаков – для большинства инженерных задач оптимально от 4 до 6 знаков после запятой.

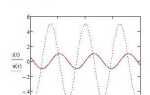
В разделе «Инструменты» включите панель быстрых функций, где доступны основные операторы для решения уравнений: solve, root, find. Это ускорит вставку необходимых блоков и формул. Рекомендуется закрепить панель для постоянного доступа.

Для удобства редактирования и проверки уравнений активируйте режим подсветки синтаксиса и автоматической проверки ошибок. Эта функция выявляет синтаксические неточности в реальном времени, что исключает ошибки при вычислениях.

Перед решением уравнений создайте рабочую область с четким разделением переменных, констант и итоговых решений. Используйте комментарии для пояснения ключевых шагов, чтобы избежать путаницы при повторном анализе документа.

Наконец, настройте параметры сохранения документа в формате, поддерживающем все математические объекты и свойства Mathcad, чтобы исключить потерю данных при повторном открытии файла.

Ввод и форматирование алгебраических уравнений

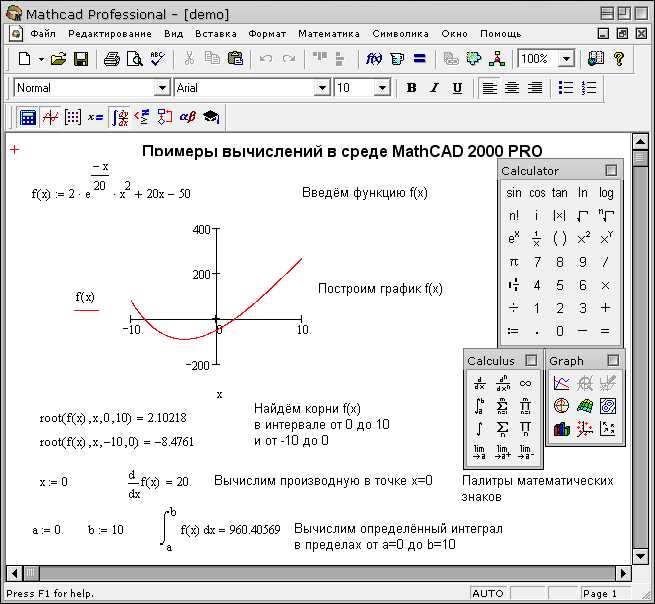
В Mathcad для ввода уравнений используйте область вычислений, активируемую нажатием клавиши «=» или щелчком в пустом месте рабочего листа. Алгебраические выражения вводятся в привычном математическом формате: переменные, операторы (+, -, *, /), степени с помощью ^ и функции. Для возведения в степень достаточно ввести, например, x^2.

Mathcad автоматически распознаёт математическую структуру и форматирует уравнения с подстрочными индексами, дробями и скобками корректно. Для группировки выражений применяйте круглые скобки (), которые корректно отображаются и учитываются при вычислениях.

Чтобы вставить дробь, используйте символ “/” между числителем и знаменателем, либо нажмите сочетание Ctrl+/, что откроет шаблон дроби для удобного ввода. Для степени с дробным показателем вводите числитель и знаменатель степени через символ дроби: например, x^(1/2) для квадратного корня.

Функции вводятся с использованием стандартных имен, например, sin(x), ln(x), sqrt(x). Mathcad автоматически распознаёт и форматирует их, отображая скобки и аргументы. Для ввода корня используйте функцию sqrt(), а не вручную вставляйте радикал.

Для обозначения неизвестных переменных используйте латинские буквы без пробелов. Mathcad чувствителен к регистру, поэтому x и X – разные переменные.

Если уравнение длинное, разбейте его на несколько строк с помощью клавиши Enter, при этом Mathcad сохранит связь между частями. Для отображения системы уравнений применяйте матричные выражения или используйте оператор «:=» для определения нескольких уравнений.

Использование функции solve для решения простых уравнений

В Mathcad для решения уравнений применяется функция solve. Она возвращает значение переменной, при котором уравнение обращается в ноль. Формат вызова: solve(уравнение, переменная).

Пример: чтобы найти корень уравнения x^2 — 4 = 0, вводят solve(x^2 - 4, x). Результат – x = ±2.

Функция работает только с уравнениями, в которых одна переменная. Если уравнение не выражено относительно переменной, предварительно рекомендуется преобразовать его так, чтобы переменная была явно выделена.

В случаях, когда уравнение содержит несколько корней, Mathcad возвращает один из них. Для поиска другого корня используют начальное приближение с помощью оператора guess.

При вводе уравнения важно соблюдать синтаксис Mathcad: операторы и переменные должны быть четко определены, а функции – корректно записаны. Ошибки в записи приведут к отсутствию решения или неправильному результату.

Для проверки решения после вызова solve подставьте найденное значение в исходное уравнение – результат должен быть близок к нулю.

Решение систем уравнений с несколькими переменными

Mathcad позволяет эффективно решать системы уравнений с несколькими переменными, используя встроенные функции и пошаговый подход.

Определите систему уравнений в виде функций, например: f1(x, y) := ..., f2(x, y) := .... Убедитесь, что переменные объявлены явно.
Используйте функцию find для решения системы: find(x, y, f1(x,y)=0, f2(x,y)=0). Mathcad возвращает численное приближение.
При наличии более двух уравнений и переменных применяйте функцию Root(), которая поддерживает системы с несколькими неизвестными.
Задайте начальные приближения переменных в функции Root() для повышения точности и ускорения сходимости.
Проверяйте корректность решения подстановкой найденных значений обратно в исходные уравнения.

Если система содержит нелинейные уравнения, убедитесь, что начальные приближения близки к реальному решению, иначе Root() может не сойтись.
Для анализа решения используйте графики функций или отображение значений ошибок |f1|, |f2|, ... в точках найденных корней.
Mathcad позволяет решать системы как алгебраические, так и дифференциальные, но дифференциальные требуют специализированных функций (rkfixed, odesolve).

Использование пошагового подхода с правильным заданием функций, выбором начальных условий и проверкой результатов обеспечивает надежное решение систем уравнений с несколькими переменными в Mathcad.

Настройка начальных приближений для численных методов

В Mathcad выбор начального приближения критически важен для устойчивости и скорости сходимости численных методов, таких как метод Ньютона или метод простой итерации. Начальное приближение вводится в виде числового значения или векторного массива в зависимости от задачи.

Для одиночных уравнений рекомендуется выбирать значение, близкое к ожидаемому корню, используя предварительный анализ графика функции с помощью встроенных графических инструментов Mathcad. Это позволяет избежать выхода алгоритма за пределы области определения и минимизировать количество итераций.

В системах уравнений начальные приближения задаются по компонентам векторного аргумента. Рекомендуется использовать приближённые решения, полученные аналитически или численно из упрощённых моделей. В Mathcad для передачи начального приближения используется оператор := с указанием вектора значений.

При работе с жёсткими системами или многократными корнями стоит уменьшить шаг итераций и уточнить начальное приближение, изменяя параметры функции и просматривая поведение решения в окрестности выбранной точки.

Mathcad позволяет сохранять и повторно использовать начальные приближения, что полезно при повторных вычислениях с изменёнными параметрами задачи. Это ускоряет процесс и снижает риск расходимости.

Если метод не сходится, рекомендуется проверить корректность и релевантность начального приближения, изменить его и повторить расчёт. В некоторых случаях полезно использовать несколько начальных приближений для поиска всех корней.

Обработка ошибок и проверка корректности решений

Mathcad позволяет автоматически выявлять и устранять ошибки в уравнениях благодаря встроенным функциям диагностики и логического контроля.

Используйте встроенную функцию isdefined() для проверки определения переменных перед расчетом. Это предотвращает ошибки из-за неопределенных значений.
При решении уравнений через solve() анализируйте сообщения об ошибках. Mathcad возвращает подробные сведения о типе ошибки (синтаксическая, арифметическая, логическая).
Проверяйте область определения функции вручную, особенно для корней и логарифмов, чтобы избежать вычислений вне допустимых значений.
Для уравнений с несколькими корнями используйте графический анализ функции, чтобы убедиться, что Mathcad не пропустил решения.
Проверяйте итоговые значения, подставляя их обратно в исходное уравнение с помощью операций подстановки и вычисления выражений.

Для повышения надежности расчетов:

Разбивайте сложные уравнения на части и проверяйте каждую на отдельность.
Используйте логические операторы и условия, чтобы обработать случаи, когда решение не существует или бесконечно.
Применяйте функцию abs() для контроля малых погрешностей при проверке решения (например, результат должен быть близок к нулю с точностью 10^-6).

В Mathcad рекомендуется всегда документировать шаги решения с комментариями, фиксировать предполагаемые значения переменных и использовать встроенный дебаггер для выявления ошибок на ранних этапах.

Экспорт и сохранение результатов решения уравнений

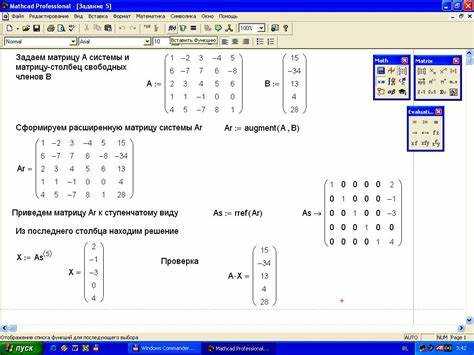
Для экспорта результатов в более универсальные форматы откройте File → Export. Рекомендуется использовать PDF, если требуется статичный отчет с сохранением оформления и графиков. При необходимости передачи численных данных в другие программы выберите формат Excel (.xlsx), который экспортирует таблицы и значения переменных.

Для экспорта отдельных фрагментов решения выделите нужный блок и используйте Copy as Image или Copy as MathML. Первый вариант сохраняет визуальное отображение, второй – позволяет вставлять формулы в редакторы, поддерживающие MathML.

Рекомендуется регулярно сохранять промежуточные результаты во избежание потери данных. Для автоматического резервного копирования активируйте опцию Auto-save в настройках Mathcad с интервалом не более 5 минут.

Вопрос-ответ:

Как в Mathcad задать уравнение для решения?

В Mathcad уравнение вводится с помощью оператора равенства (=). Для задания уравнения необходимо ввести выражение с переменной, например, x^2 + 3*x — 5 = 0. Затем можно использовать функции решения, указав уравнение и переменную, которую нужно найти.

Какие методы решения уравнений доступны в Mathcad и как выбрать подходящий?

Mathcad предлагает несколько способов решения уравнений: аналитический и численный. Аналитический метод подходит для простых уравнений с известными формулами решения, например, квадратных. Для более сложных или нелинейных уравнений применяется численное решение с помощью функций, таких как root или find. Выбор зависит от типа уравнения и требуемой точности результата.

Можно ли решать в Mathcad системы уравнений? Как это сделать пошагово?

Да, Mathcad позволяет решать системы уравнений. Для этого нужно последовательно ввести каждое уравнение в виде выражения с равенством, затем использовать функцию решения системы, передав ей список уравнений и переменных. В пошаговом режиме сначала вводятся все уравнения, потом указываются переменные для поиска, и, наконец, запускается вычисление. В результате получится набор значений переменных, удовлетворяющих системе.

Что делать, если Mathcad не находит решение уравнения или выдаёт ошибку?

В таких случаях стоит проверить корректность записи уравнения и диапазон поиска переменных. Если используется численный метод, возможно, нужно задать начальное приближение ближе к предполагаемому корню. Также важно удостовериться, что уравнение действительно имеет решение в заданной области. Иногда помогает разбиение задачи на более простые части или использование аналитического подхода, если он доступен.