Как вычислить производную в maple

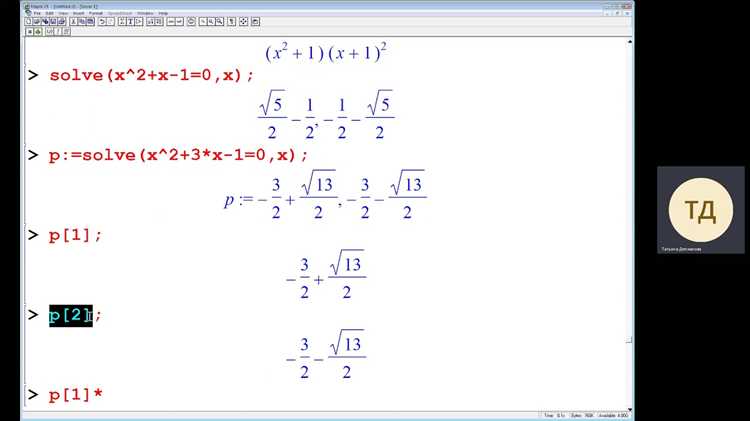
Maple предоставляет мощный инструмент для вычисления производных, позволяя обойтись минимальным набором команд. Основная функция для дифференцирования – diff, которая работает с любыми выражениями и переменными.

Для вычисления производной достаточно указать функцию и переменную, по которой производится дифференцирование. Например, diff(f(x), x) вернёт первую производную функции f по x. Maple автоматически упрощает результат, что позволяет сразу использовать его для дальнейших вычислений или построения графиков.

Если требуется найти производную более высокого порядка, достаточно добавить соответствующий параметр: diff(f(x), x$n$), где n – порядок производной. Такая лаконичность значительно ускоряет работу и снижает вероятность ошибок в вычислениях.

Как задать функцию для дифференцирования в Maple

В Maple функция задаётся через оператор := с использованием переменных. Например, f := x -> x^3 + 2*x^2 — 5; определяет функцию f(x). Обязательно указывайте переменную после стрелки «->», иначе Maple не распознает зависимость функции.

Для функций нескольких переменных используйте синтаксис с несколькими аргументами: g := (x,y) -> x^2 + y^2. Дифференцирование по конкретной переменной будет корректным только при такой записи.

Можно задать функцию через выражение, привязанное к переменной, например: f := x^2 + 3*x — 1. Однако при дифференцировании потребуется указывать переменную явно, что менее удобно и не рекомендуется для сложных функций.

Для упрощения работы с параметрами лучше сразу объявлять функцию через стрелочный синтаксис, чтобы избежать ошибок при вычислении производной и последующей подстановке значений.

Использование команды diff для вычисления производной

В Maple команда diff служит для точного и быстрого вычисления производных функций. Она поддерживает дифференцирование по одной или нескольким переменным с возможностью указания порядка производной.

• Синтаксис базовый: diff(функция, переменная) – вычисляет первую производную функции по указанной переменной.
• Производная высшего порядка: diff(функция, переменная$n$), где n – порядок производной, например, diff(f(x), x$3) – третья производная по x.
• Частные производные по нескольким переменным: diff(f(x,y), x, y) вычисляет смешанную производную по x и y.

Команда diff работает с выражениями как в символической форме, так и с заданными функциями. Для функций, определённых как f := x -> x^3 + 2*x;, рекомендуется использовать именно такой вид для корректного вычисления.

1. Определите функцию или выражение, например, f := x^4 + 3*x^2;
2. Вызовите производную: diff(f, x); – результат будет 4*x^3 + 6*x
3. Для функции с несколькими переменными: diff(x^2*y + y^3, x); вернёт 2*x*y

Для численных вычислений производных diff не применяется напрямую. В этом случае используют дополнительные пакеты или приближённые методы.

Вычисление производной сложной функции в Maple

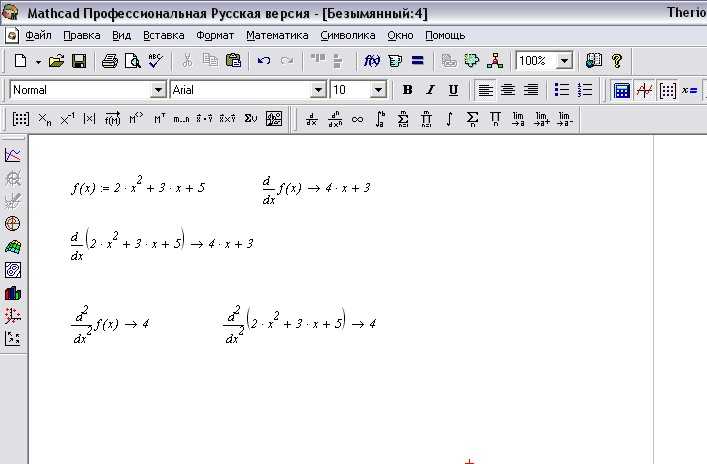
Для дифференцирования сложных функций в Maple применяется команда diff, позволяющая работать с многочленами, тригонометрическими, экспоненциальными и логарифмическими выражениями. Важно точно задать функцию с помощью :=, а не =, чтобы избежать вычисления сразу при объявлении.

Пример задания сложной функции:

f := x -> sin(x^2) * exp(x);

Для нахождения производной используйте diff с передачей функции и переменной:

df := diff(f(x), x);

Maple автоматически применит правило цепочки для внутренней функции x^2, корректно вычислив производную сложного выражения.

Если требуется вычислить производную высших порядков, укажите степень как третий аргумент:

diff(f(x), x $ 3);

Для упрощения результата полезно применять команду simplify, что делает выражение более читаемым и удобным для дальнейшего анализа.

При работе с несколькими переменными задавайте функцию с соответствующим числом аргументов и указывайте переменную дифференцирования явно, например:

g := (x,y) -> ln(x^2 + y^2);

diff(g(x,y), x);

В случаях, когда функция сложна для стандартного дифференцирования, можно разбить её на части, вычислить производные отдельно и затем объединить, что минимизирует ошибки и повышает контроль над процессом.

Производная от функции нескольких переменных в Maple

Для вычисления частных производных функций нескольких переменных в Maple применяется команда diff. Синтаксис включает функцию и переменные, по которым берутся производные. Например, для функции f:= (x,y) -> x^2*y + sin(x*y) частная производная по x вычисляется командой diff(f(x,y), x), а по y – diff(f(x,y), y).

Для производных высших порядков указываются переменные и количество дифференцирований через запятую. Так, вторая производная по x вычисляется как diff(f(x,y), x$2), смешанная – diff(f(x,y), x, y). Maple автоматически упрощает результат.

Если функция задана в явном виде, можно использовать команду D, создавая дифференциальный оператор. Для функции f оператор по x задается как Dx:= D[1](f), после чего вычисление частной производной сводится к вызову Dx(x,y).

Для символического дифференцирования по нескольким переменным одновременно применяется команда diff(f(x,y), [x,y]), возвращающая вектор частных производных.

В случаях, когда функция задана через выражение, удобно использовать явное указание переменных: diff(x^2*y + sin(x*y), x). Maple поддерживает дифференцирование по параметрам и функциям, включая производные по сложным выражениям.

Как вычислить производную высшего порядка

В Maple для вычисления производных высшего порядка используется функция diff. Для производной n-го порядка достаточно указать функцию, переменную и порядок дифференцирования.

Синтаксис:

diff(f(x), x$n), где f(x) – функция, x – переменная, n – порядок производной.

Пример вычисления второй производной функции f(x) = x^4 + 3*x^2:

diff(x^4 + 3*x^2, x$2);

Результат будет 12*x^2 + 6.

Если функция зависит от нескольких переменных, можно вычислить смешанную производную, например:

diff(f(x,y), x$2, y$1);

вычислит производную второго порядка по x и первого по y.

Для хранения результата производной в переменную следует использовать оператор присваивания, например:

d2 := diff(f(x), x$2);

Это удобно при дальнейших вычислениях или преобразованиях.

Автоматическое упрощение результата производной

В Maple вычисление производной с помощью команды diff не всегда приводит к окончательно упрощённому виду выражения. Для автоматического упрощения результата применяется функция simplify, которая сокращает выражения, упрощает дроби и устраняет избыточные скобки.

После вычисления производной рекомендуется сразу использовать simplify или simplify(<выражение>, symbolic) для более глубокого алгебраического упрощения. Опция symbolic позволяет Maple применять более сложные преобразования, учитывая свойства функций.

Если требуется сохранение структуры выражения, но с сокращением числовых коэффициентов, применяется combine, который объединяет подобные члены и выражения с одинаковыми основаниями. Для тригонометрических производных полезна функция trigsimp, автоматически преобразующая тригонометрические выражения к более компактному виду.

Для автоматизации процесса часто используют цепочку функций: diff → simplify → expand → combine. Такой подход позволяет получить максимально понятный и компактный результат без ручных преобразований.

Рекомендуется избегать использования только evalf после дифференцирования, так как это приводит к численной оценке, а не к упрощению аналитического выражения.

Пример:

simplify(diff(sin(x)^2 + cos(x)^2, x)) сразу возвращает 0, что свидетельствует о корректном распознавании тождеств и упрощении.

Сравнение численного и символьного дифференцирования в Maple

В Maple существуют два основных подхода к вычислению производных: численный и символьный. Каждый из них обладает специфическими особенностями и применяется в зависимости от задачи.

• Символьное дифференцирование выполняется командой diff. Оно дает точное аналитическое выражение производной, сохраняя функциональную зависимость.
• Численное дифференцирование реализуется через команды типа evalf(D(f)(x0)) или функции с конечными разностями. Здесь результат – приближенное значение производной в заданной точке.

Рекомендации по выбору метода в Maple:

1. Для анализа общих свойств функции, оптимизации или построения графиков предпочтительно использовать символьное дифференцирование, поскольку оно обеспечивает формулу с полной точностью.
2. Если функция задана сложным числовым алгоритмом или не имеет явного аналитического вида, численное дифференцирование позволяет получить производную в конкретной точке быстро и с контролируемой точностью.
3. Символьные производные могут привести к громоздким выражениям, что влияет на производительность. В таких случаях целесообразно вычислить производную символически, а затем численно оценить в нужных точках.
4. Численное дифференцирование требует настройки шага аппроксимации для минимизации ошибки, при этом Maple автоматически использует оптимальные значения, но при нестандартных задачах рекомендуется проверять устойчивость результатов.

Подводя итог, Maple обеспечивает эффективные инструменты для обеих техник, а выбор зависит от наличия аналитической формулы, требований к точности и скорости вычислений.

Экспорт результата производной из Maple для дальнейшей работы

Для передачи результата вычисления производной из Maple в другие приложения или документы используйте команды экспорта, ориентированные на нужный формат. Самый универсальный способ – сохранить выражение производной в виде строки с помощью команды StringTools[Trim](convert(diff(f(x), x), string)). Это позволяет получить читаемое текстовое представление производной.

Если необходимо экспортировать результат для систем компьютерной алгебры или программирования, используйте команду exportexpr или print`printf` с указанием формата. Например, для экспорта в LaTeX применяйте latex(diff(f(x), x)), что упростит интеграцию результата в научные публикации.

Для передачи данных в текстовые файлы Maple предлагает функцию save с указанием имени переменной и файла: save diff_result, "filename.m". В файле сохранится объект производной, который затем можно загрузить в другую сессию Maple через read "filename.m".

При необходимости интеграции с языками программирования (например, Python или MATLAB) используйте экспорт в формат MathML или XML через пакет CodeGeneration: CodeGeneration[Export](diff(f(x), x), format = mathml, filename = "derivative.xml"). Это обеспечивает корректное восприятие выражения другими системами.

Для быстрого копирования в буфер обмена применяйте команду copy(expr) после вычисления производной, что позволяет сразу вставить результат в текстовые редакторы или код без промежуточных файлов.

Вопрос-ответ:

Как вычислить производную функции в Maple простым способом?

В Maple для вычисления производной достаточно использовать встроенную команду diff. Нужно записать выражение функции, а затем вызвать diff с этим выражением и переменной, по которой берётся производная. Например, diff(x^3, x) выдаст 3*x^2.

Можно ли в Maple вычислить производную сложной функции, например, с тригонометрическими или экспоненциальными выражениями?

Да, Maple поддерживает вычисление производных для любых функций, включая тригонометрические, логарифмы, экспоненты и даже сложные составные выражения. Достаточно указать функцию целиком в команде diff. Например, diff(sin(x^2) + exp(x), x) Maple автоматически применит правила дифференцирования и выдаст результат.

Как получить производную функции в Maple с сохранением результата для дальнейших вычислений?

Чтобы сохранить вычисленную производную для последующего использования, достаточно присвоить результат переменной. Например, y := diff(x^4 + 2*x, x); После этого в переменной y будет храниться выражение производной, и его можно использовать в других вычислениях или построении графиков.

Возможно ли получить производную в Maple по нескольким переменным одновременно и как это сделать?

Да, Maple позволяет вычислять частные производные по разным переменным. Для этого в команде diff указывают функцию и переменные с количеством дифференцирований по каждой из них. Например, diff(f(x,y), x, y) вычисляет смешанную производную сначала по x, затем по y. Это удобно для работы с функциями нескольких переменных.