Как взять интеграл в maple

Maple – мощная среда для символьных вычислений, позволяющая находить определённые и неопределённые интегралы с полной детализацией. В отличие от калькуляторов, Maple предоставляет не только результат, но и промежуточные шаги, что важно для анализа методов интегрирования.

Чтобы найти интеграл в Maple, используется команда int(). Например, int(sin(x), x) возвращает -cos(x). Для определённого интеграла указываются пределы: int(x^2, x = 0..2). Команда Student[Calculus1][ShowSolution]() раскрывает пошаговое решение. Её можно применять к простым и составным выражениям, если заранее активировать пакет with(Student[Calculus1]).

Если выражение содержит параметры или требует подстановки, Maple позволяет задавать условия через assume() или assuming. Это особенно полезно при вычислении интегралов с переменными пределами или при наличии особенностей у подынтегральной функции. Например: int(1/(x^2 + a^2), x) при assuming a > 0 возвращает результат с арктангенсом.

Пошаговое решение может быть недоступно для интегралов, не имеющих элементарного первообразного. В таких случаях Maple предложит численный результат с помощью evalf(Int(…)) или приблизительную оценку через Student[NumericalAnalysis][SimpsonRule]().

Использование Maple для интегрирования экономит время при подготовке решений и разборе типовых задач. Особенно полезна функция Maplet для визуального отображения шагов, если активирован интерфейс с поддержкой графики. Это делает Maple удобным инструментом при обучении и подготовке к экзаменам.

Как вычислить определённый интеграл с помощью команды int

Для вычисления определённого интеграла в Maple используется команда int с указанием пределов интегрирования. Синтаксис: int(f(x), x = a..b);, где f(x) – подынтегральная функция, a и b – нижний и верхний пределы соответственно.

Пример: int(sin(x)^2, x = 0..Pi);. Maple вернёт результат Pi/2.

Если функция содержит параметры, Maple возвращает выражение с ними. Пример: int(exp(-a*x), x = 0..infinity); даёт 1/a при условии Re(a) > 0. Чтобы задать это явно, используйте assume(a > 0); перед вызовом int.

Для численного приближённого значения добавьте evalf: evalf(int(sqrt(1 + x^4), x = 0..2));.

Если необходимо увидеть пошаговое решение, используйте команду Student[Calculus1][ShowSolution](int(...)); с теми же аргументами.

Для обозначения бесконечности используйте infinity и -infinity. Пример: int(1/(1 + x^2), x = -infinity..infinity); даст Pi.

Если результат не выражается через элементарные функции, Maple оставит его в виде int(...). Пример: int(exp(-x^2), x = 0..1); остаётся в неопределённой форме, но evalf вернёт численное значение.

Как задать неопределённый интеграл и получить общий вид первообразной

Для вычисления неопределённого интеграла в Maple используется команда int. Синтаксис следующий:

int(выражение, переменная);

Например, чтобы найти общий вид первообразной функции sin(x), вводится:

int(sin(x), x);

Результат: -cos(x). Это и есть общая форма первообразной без добавления произвольной константы – Maple по умолчанию её не отображает.

• Для выражений, содержащих параметры, Maple выполняет интегрирование по указанной переменной. Пример: int(a*x^2, x); – результат (1/3)*a*x^3.
• Чтобы Maple явно показал шаги, используется команда Student[Calculus1][ShowSolution]. Пример:

with(Student[Calculus1]):
ShowSolution(int(x^2, x));

Пошаговое решение появится в виде последовательных преобразований.

При вводе сложных выражений обязательно используйте символы умножения * и корректные скобки. Пример: int((x+1)*exp(x), x);.

Если Maple не может найти элементарную первообразную, он возвращает выражение в форме int(...) без вычисления. Это означает, что интеграл выражается через специальные функции или не берётся в элементарных функциях.

• Для задания произвольной константы в ответе вручную прибавьте +C – Maple это не делает автоматически.
• Переменная должна быть явно указана. int(x^2); вызовет ошибку – нужно int(x^2, x);

Как задать переменные и пределы интегрирования вручную

В Maple для задания переменных и пределов интегрирования вручную используется команда int. Синтаксис: int(выражение, переменная=нижний..верхний).

Например, чтобы вычислить определённый интеграл функции x^2 по переменной x от 0 до 5, используйте:

int(x^2, x=0..5);

Для неопределённого интеграла указывайте только переменную без пределов:

int(sin(x), x);

Если переменных несколько, вложите интегралы друг в друга. Например, двойной интеграл по x от 0 до 1 и по y от 0 до 2:

int(int(x*y, y=0..2), x=0..1);

Порядок интегрирования важен. Меняя его, переписывайте пределы с учётом области интегрирования.

Для явного указания переменной используйте форму с квадратными скобками: int(f, [x=a..b]). Это полезно при множественном интегрировании, например:

int(f, [x=0..1, y=0..2]);

Если пределы содержат переменные, Maple обрабатывает их символически. Например:

int(x, x=a..b);

Для изменения переменной в уже введённой команде удобно использовать контекстное меню или повторный ввод с редактированием.

Как вычислить кратный интеграл в двумерном и трёхмерном случае

В Maple вычисление кратных интегралов выполняется с помощью команды int для определённых и неопределённых интегралов. Для кратных интегралов используется вложенная структура вызовов int или синтаксис с указанием нескольких переменных и границ в одной команде.

Пример 1: Двойной интеграл по прямоугольной области

Вычисление выражения ∬(x + y) dx dy, где x от 0 до 2, y от 1 до 3:

int(int(x + y, x = 0 .. 2), y = 1 .. 3);

Результат: 16

Пример 2: Двойной интеграл по области, заданной неравенствами

Интеграл ∬(x*y) dx dy по области x от 0 до y, y от 0 до 1:

int(int(x*y, x = 0 .. y), y = 0 .. 1);

Результат: 1/8

Пример 3: Тройной интеграл по параллелепипеду

Интеграл ∭(x + y + z) dx dy dz, где x от 0 до 1, y от 0 до 2, z от 0 до 3:

int(int(int(x + y + z, x = 0 .. 1), y = 0 .. 2), z = 0 .. 3);

Результат: 27

Пример 4: Тройной интеграл по области, заданной неравенствами

Область: x от 0 до y, y от 0 до z, z от 0 до 1. Интеграл ∭(x*z) dx dy dz:

int(int(int(x*z, x = 0 .. y), y = 0 .. z), z = 0 .. 1);

Результат: 1/24

Рекомендации

• Сначала указываются внутренние границы, затем внешние.
• Порядок интегрирования влияет на структуру границ, особенно при зависимых переменных.
• Для областей, заданных через неравенства, важно правильно выбрать пределы переменных, отражающие вложенность.
• Если используется int без указания границ, результатом будет символическое выражение.

Как упростить результат интегрирования с помощью встроенных функций Maple

После выполнения интегрирования в Maple результат может содержать громоздкие выражения, которые затрудняют дальнейшую работу. Для упрощения результата применяются следующие встроенные функции:

• simplify(expr) – основная команда для упрощения. Применяется к результату интеграла:

  simplify(∫(sin(x)^2, x))

  Maple вернёт x/2 - sin(2x)/4.

• combine(expr) – объединяет дроби, логарифмы, тригонометрические выражения:

  combine(ln(x) + ln(y))

  Возвращает ln(x*y).

• expand(expr) – раскрывает скобки и распределяет множители:

  expand(∫((x + 1)^2, x))

  Выдаёт интеграл от x^2 + 2x + 1.

• factor(expr) – факторизует выражение:

  factor(x^2 - 1)

  Возвращает (x - 1)(x + 1).

• convert(expr, form) – преобразует выражение к заданной форме:
  • convert(expr, exp) – превращает тригонометрические выражения в экспоненциальные;
  • convert(expr, trig) – обратно, экспоненты в синусы/косинусы;
  • convert(expr, radical) – преобразует степени в корни.
• normal(expr) – сокращает дробные выражения:

  normal((x^2 - 1)/(x - 1))

  Результат – x + 1.

• simplify(expr, symbolic) – активирует более глубокую символьную обработку:

  simplify(∫(1/(x^2 + 1)^2, x), symbolic)

  Даёт точную символьную форму без численного приближения.

Для сложных выражений полезно применять комбинации функций. Например:

simplify(combine(expand(∫((x + 1)^2/(x^2 + 1), x))))

Эта цепочка позволяет сначала раскрыть скобки, затем объединить дроби и упростить результат.

Как визуализировать область интегрирования и график функции

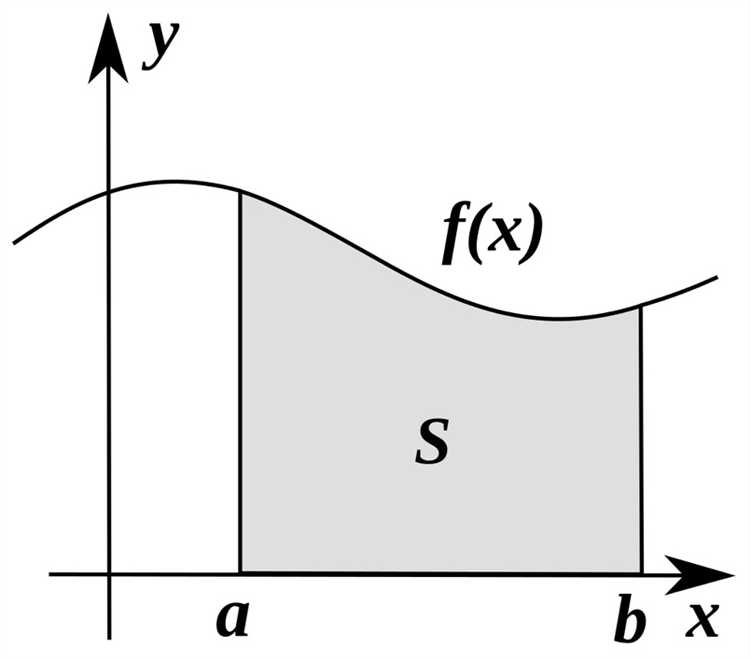
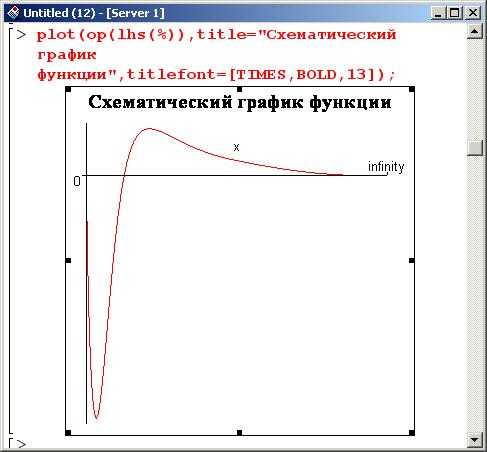
Для построения графика функции в Maple используется команда plot. Например, для функции f := x -> sin(x) график строится так: plot(f, x = 0 .. Pi). Важно указывать границы переменной для точного отображения.

Чтобы визуализировать область интегрирования в двойных интегралах, применяется команда plots[regionplot]. Она позволяет задать область в координатах, например: plots[regionplot](x^2 + y^2 ≤ 1, x = -1 .. 1, y = -1 .. 1) построит круг радиуса 1.

Для объединения графика функции и области интегрирования используют команду display из пакета plots. Сначала строят график функции через plot3d, затем создают график области с помощью plottools[polygon] или plots[regionplot], после чего объединяют через display([plot1, plot2]).

При построении трехмерного графика интегрируемой функции важно установить параметры сетки и прозрачность, чтобы не перекрывать область интегрирования. Например: plot3d(f(x,y), x=a..b, y=c..d, style=surface, transparency=0.5).

Для точного отображения границ интегрирования рекомендуется использовать явные уравнения или неравенства, соответствующие области. В случае сложных областей удобно комбинировать несколько условий в regionplot с логическими операторами.

Вопрос-ответ:

Как в Maple задать интеграл для пошагового решения?

Чтобы получить поэтапное вычисление интеграла в Maple, нужно сначала ввести выражение с командой интеграла, например, `int(f(x), x)`. Далее используется функция `Student[Calculus1]:` или команда `step` из пакета, позволяющего выводить промежуточные шаги. Важно подключить соответствующий пакет командой `with(Student[Calculus1]):` перед вычислением. После этого Maple покажет последовательность действий, которые он выполняет, чтобы найти интеграл.

Можно ли увидеть, как Maple разбивает сложный интеграл на более простые части?

Да, Maple умеет демонстрировать промежуточные этапы решения, включая разбиение интеграла на более простые слагаемые. Для этого используется специальный пакет, позволяющий отображать разложение по частям, замены переменных и применение основных правил интегрирования. При вычислении интеграла с помощью команды `Student[Calculus1][IntStep](…)` Maple покажет, какие преобразования он проводит, что помогает понять логику и структуру решения.

Как в Maple получить подробный разбор подстановок при интегрировании?

В Maple для этого можно использовать функцию из учебного пакета, которая раскрывает подстановки, сделанные в процессе решения. Обычно это пакет `Student[Calculus1]`. После загрузки пакета команда `IntStep` выведет, какие именно замены переменных или подстановки были применены, вместе с обоснованием. Это удобно для изучения метода подстановки и для понимания, как Maple упрощает интеграл перед вычислением.

Можно ли в Maple увидеть, как происходит интегрирование по частям с объяснениями?

Да, Maple может показать пошаговое выполнение метода интегрирования по частям, если использовать соответствующий учебный пакет. Вызов функции `Student[Calculus1][IntStep]` для интеграла, который требует этот метод, продемонстрирует, какую часть функции Maple выбрала в качестве u и dv, как вычисляются производные и интегралы, и как строится итоговое выражение. Это помогает понять логику метода на конкретных примерах.

Что делать, если Maple не показывает шаги решения интеграла?

Если шаги решения не выводятся, скорее всего, не подключен нужный пакет или используется команда, которая сразу даёт конечный результат без промежуточных этапов. Чтобы решить проблему, нужно выполнить команду `with(Student[Calculus1]):` и использовать функции из этого пакета, например, `IntStep`. Также стоит проверить, что интеграл можно разложить по шагам — иногда слишком сложные выражения требуют дополнительной подготовки или разбивки на части.

Как в Maple пошагово вычислить определённый интеграл с помощью встроенных команд?

В Maple для вычисления определённого интеграла сначала нужно задать функцию и пределы интегрирования. Например, если у вас функция f(x), а интеграл берётся от a до b, вводят команду вида `int(f(x), x = a .. b)`. Чтобы увидеть пошаговое решение, можно использовать пакет Student[Calculus1] и команду `Student[Calculus1]:StepIntegral(f(x), x = a .. b)`. Эта команда выведет последовательность действий: разбиение задачи, применение формул интегрирования и подстановку пределов. Если такой пакет не загружен, его можно подключить через `with(Student[Calculus1])`. После этого Maple покажет, как разбивается интеграл, какие правила используются, и как вычисляется конечный результат. Этот способ помогает понять, как происходит вычисление, и служит обучающим инструментом, если нужно разобраться в каждом этапе интегрирования.