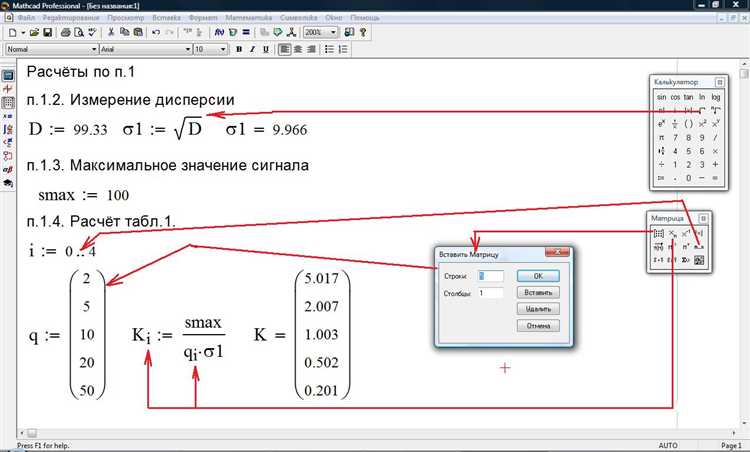
В Mathcad функция арккосинуса обозначается как arccos или acos и возвращает угол в радианах по значению косинуса. Диапазон допустимых значений аргумента – от -1 до 1, что соответствует области определения функции. При вводе выражения важно соблюдать синтаксис Mathcad, чтобы получить корректный результат.
Для вычисления арккосинуса в Mathcad достаточно использовать встроенную функцию: arccos(x), где x – числовое значение или выражение в допустимом диапазоне. Если аргумент выходит за пределы [-1,1], программа выдаст ошибку или неверное значение. Следует учитывать, что по умолчанию Mathcad возвращает угол в радианах, но при необходимости можно перевести результат в градусы с помощью оператора преобразования.
В практических примерах важно учитывать контекст использования: вычисление углов в тригонометрических задачах, обработка сигналов, геометрические построения. Для удобства и точности рекомендуется использовать встроенные средства Mathcad для проверки области определения аргумента и автоматического преобразования единиц измерения.
Синтаксис функции arccos в Mathcad и особенности ввода
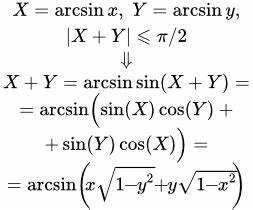
В Mathcad для вычисления арккосинуса используется функция arccos(x) или её синоним acos(x). Аргумент x должен быть числом или выражением, возвращающим число в диапазоне от –1 до 1, так как вне этого интервала значение функции не определено.
Для ввода функции arccos необходимо набрать arccos или acos, после чего автоматически появится пара круглых скобок. Внутрь скобок вводится аргумент функции. Mathcad воспринимает знаки и операции внутри скобок как стандартное математическое выражение.
Если аргумент – вектор или матрица, функция применится поэлементно, возвращая соответствующую структуру с арккосинусами элементов. Для корректной работы с массивами важно, чтобы все значения находились в допустимом диапазоне.
Ошибки при вводе чаще всего связаны с выходом аргумента за пределы интервала [–1, 1], в таких случаях Mathcad выдаст предупреждение о невозможности вычисления. Следует проверять область определения перед вызовом arccos.
Как вычислить арккосинус числа в градусах и радианах в Mathcad
В Mathcad функция арккосинуса обозначается как arccos(x) или acos(x). По умолчанию результат вычисляется в радианах. Для получения значения в градусах необходимо выполнить преобразование.
Чтобы вычислить арккосинус в радианах, достаточно записать выражение:
theta := arccos(x)
где x – число в диапазоне от -1 до 1, theta – угол в радианах.
Для перевода радианов в градусы используйте умножение на константу 180/π или встроенную функцию преобразования углов, если она доступна. Пример:
theta_deg := arccos(x) * 180 / π
В Mathcad π задаётся через встроенную константу π. Обязательно проверьте, что значение x не выходит за пределы допустимого диапазона, иначе функция вернёт ошибку.
Для упрощения работы можно определить пользовательскую переменную, например:
arccos_deg(x) := arccos(x) * 180 / π
Теперь вызов arccos_deg(0.5) вернёт угол в градусах.
Обработка ошибок при вводе значений вне диапазона функции arccos

Функция arccos в Mathcad корректно вычисляется только для аргументов в диапазоне от -1 до 1 включительно. Значения вне этого интервала вызывают ошибку вычисления или возвращают неопределённый результат. Для предотвращения сбоев следует реализовать проверку входных данных перед вызовом arccos.
В Mathcad для обработки таких ситуаций удобно применять условные операторы:
if (x < -1) or (x > 1) then "Ошибка: значение вне диапазона" else arccos(x)
Также полезно автоматизировать обработку с помощью функций, возвращающих осмысленный результат при ошибке, например, возвращая значение по умолчанию или предупреждение.
В случаях обработки массивов значений следует применять элементную проверку с использованием функции vector и операторов цикла, чтобы избежать прерывания вычислений из-за одного некорректного аргумента.
Использование arccos для решения тригонометрических уравнений в Mathcad
В Mathcad функция arccos обозначается как acos и вычисляет обратный косинус значения, возвращая угол в радианах или градусах в зависимости от установок документа. Для решения уравнения вида cos(x) = a, где a – заданное число, используйте выражение x := acos(a). Это даст один из возможных корней.
Так как функция косинуса периодична с периодом 2π, общее решение записывается через основное значение arccos и прибавление целых кратных 2π, а также с учётом симметрии косинуса:
x = ±acos(a) + 2πn, n ∈ ℤ
В Mathcad для генерации множества корней можно использовать оператор суммирования с параметром n или задать массив значений, например:
n := -3..3
x := acos(a) + 2π·n
x2 := -acos(a) + 2π·n
Данная запись выведет два массива решений, покрывающих оба набора корней уравнения.
При работе с углами в градусах сначала установите единицы измерения документа в градусы через меню, затем используйте функцию acos без дополнительных преобразований, результаты сразу будут в градусах.
Важно контролировать область определения функции arccos: аргумент должен лежать в интервале [-1,1]. Для значений вне этого диапазона Mathcad вернёт ошибку, что необходимо учитывать при подготовке уравнений к решению.
При составлении уравнений с несколькими тригонометрическими слагаемыми рекомендуется изолировать косинус одного выражения, чтобы применить acos к единственному числовому аргументу. В противном случае следует использовать численные методы решения, встроенные в Mathcad.
Примеры применения arccos для анализа данных и построения графиков
Функция arccos в Mathcad позволяет эффективно решать задачи, связанные с вычислением углов на основе известных косинусов, что востребовано в инженерных расчетах и научном анализе.
- Определение углов между векторами
При работе с трехмерными данными часто требуется найти угол между двумя векторами. В Mathcad это делается по формуле:
θ = arccos((A·B) / (|A|·|B|)). Для расчёта скалярного произведения и норм векторов применяются встроенные функции. Такой подход позволяет анализировать пространственные взаимосвязи, например, в механике и робототехнике. - Анализ фазовых сдвигов в сигналах
В электронике arccos помогает определить фазовый угол между сигналами на основе их корреляции. В Mathcad на основе измеренных данных косинусного сходства строится график зависимости фазы от времени, что упрощает диагностику и настройку систем.
- Вычисление углов наклона в геометрических моделях
Для анализа формы поверхности или профиля арки arccos используется для нахождения угла наклона между касательными и опорными линиями. В Mathcad строятся графики изменения угла по длине объекта, что важно при проектировании конструкций.
Для построения графиков с использованием arccos рекомендуется:
- Предварительно проверить область допустимых значений аргумента – она должна находиться в диапазоне [-1, 1].
- Использовать параметрические зависимости, чтобы график отражал изменения угла при варьировании исходных данных.
- Комбинировать arccos с функциями plot и create to plot для удобного отображения результатов и их анализа.
Особенности работы с комплексными числами и arccos в Mathcad
В Mathcad функция arccos поддерживает комплексные аргументы, что позволяет работать с числами, выходящими за пределы действительной оси. При вводе комплексного значения аргумента arccos возвращает комплексный результат, основанный на формуле:
arccos(z) = -i * ln(z + sqrt(z² — 1)), где z – комплексное число.
Важно учитывать: Mathcad использует главную ветвь комплексного логарифма, поэтому результаты могут иметь разрывы при переходе через ветвь. Для корректной интерпретации значений рекомендуется избегать вычислений на ветвях с неоднозначной трактовкой.
Для корректной работы с комплексными аргументами перед вызовом arccos необходимо убедиться, что входное значение задано в формате комплексного числа Mathcad, например, с использованием функции complex(x, y) или напрямую вводя выражение с i.
При анализе результатов arccos от комплексных чисел следует учитывать, что в Mathcad аргументы и результаты представлены в виде комплексных чисел с действительной и мнимой частями. Для получения отдельно действительной или мнимой части используют функции real() и imag().
Если необходимо ограничить вычисления в области действительных чисел, следует проверить условие |z| ≤ 1, иначе arccos перейдет в комплексную область, что может вызвать неожиданные результаты. В задачах с комплексными аргументами рекомендуется использовать встроенные средства визуализации, чтобы отслеживать поведение функции на комплексной плоскости.
Вопрос-ответ:
Как правильно ввести функцию arccos в Mathcad для вычисления обратного косинуса?
В Mathcad для вычисления арккосинуса используется функция acos(). Чтобы получить значение arccos(x), необходимо ввести acos(x), где x — число или выражение, для которого требуется найти обратный косинус. Важно, чтобы аргумент был в диапазоне от -1 до 1, иначе результат будет неопределён.
Можно ли получить результат функции arccos в градусах, а не в радианах в Mathcad?
Да, Mathcad по умолчанию выводит результат арккосинуса в радианах. Чтобы получить угол в градусах, нужно либо использовать встроенную функцию для преобразования радианов в градусы (например, умножить на 180/π), либо задать настройку угловой меры в Mathcad на градусы через меню параметров документа.
Что делать, если при вводе acos(x) в Mathcad появляется ошибка или неожиданное значение?
Ошибка может возникать, если значение x выходит за пределы допустимого диапазона [-1, 1]. В таких случаях функция acos() не может быть вычислена. Для устранения ошибки проверьте входные данные и убедитесь, что они соответствуют области определения арккосинуса. Также стоит проверить правильность написания функции и формат входных данных.
Как можно использовать arccos в Mathcad для решения тригонометрических уравнений?
В Mathcad функцию arccos удобно применять для нахождения угла, если известен косинус этого угла. Например, если уравнение содержит cos(θ) = a, то для решения можно записать θ = acos(a). После этого можно подставить конкретные значения или работать с выражениями, учитывая особенности области определения функции и диапазон углов.
Можно ли в Mathcad применять arccos к массивам данных или векторным переменным?
Да, Mathcad позволяет использовать функцию acos() для массивов или векторов. В этом случае функция применяется поэлементно ко всем значениям массива. Например, если у вас есть вектор значений косинусов, вызов acos() к этому вектору вернёт вектор углов. Главное — убедиться, что все элементы находятся в пределах от -1 до 1.