Mathcad предоставляет встроенные инструменты для точного ввода и решения дифференциальных уравнений, позволяя быстро формализовать модели динамических процессов. В отличие от текстовых редакторов, Mathcad использует математические выражения в привычном виде, что существенно упрощает работу с уравнениями, включающими производные различных порядков.
Для начала важно правильно определить переменные и функции, задать начальные или граничные условия, а затем использовать встроенную функцию ODE или аналогичные методы численного решения. Каждое дифференциальное уравнение записывается с использованием оператора производной d/dx() или его сокращений, что исключает ошибки интерпретации и ускоряет расчет.
Особое внимание уделяется синтаксису Mathcad: скобки, порядок операций и единицы измерения должны быть заданы корректно, чтобы избежать ложных результатов. Эта инструкция подробно описывает процесс от создания переменных до запуска численного решения, обеспечивая стабильность и точность вычислений без необходимости обращения к дополнительной литературе.
Запись дифференциальных уравнений в Mathcad: пошаговая инструкция
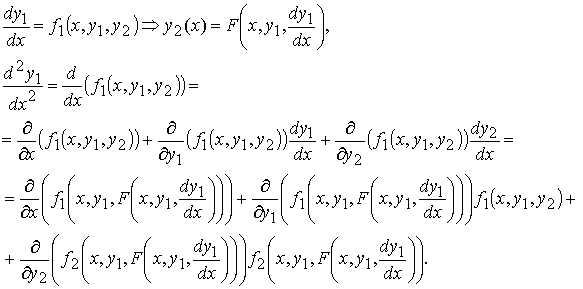
Для начала откройте новый рабочий лист Mathcad. Перейдите к месту, где планируете ввести уравнение.
Введите функцию, например, y(x), используя синтаксис: y(x) :=
Чтобы задать производную, используйте клавишу Ctrl + D (для версии Mathcad Prime) или кнопку производной на панели инструментов. Введите знак дифференцирования, например y'(x) для первой производной, y»(x) для второй.
Пример записи уравнения первого порядка: y'(x) = -2*y(x) + sin(x). Для более высокого порядка используйте y»(x) и укажите соответствующее равенство.
Если уравнение содержит несколько переменных, уточните, что дифференцирование происходит по x, например: ∂y/∂x или y'(x).
Для записи систем дифференциальных уравнений используйте массивы функций и массивы уравнений, вводя каждое уравнение с новой строки или отделяя точкой с запятой.
После ввода уравнения назначьте начальные условия через оператор :=, например y(0) := 1.
Проверьте синтаксис – Mathcad подсвечивает ошибки. Исправьте их до запуска вычислений.
Для численного решения примените встроенную функцию odeSolve, укажите уравнение, переменную и начальные условия.
Такой подход гарантирует корректное и точное введение дифференциальных уравнений в Mathcad без использования дополнительных скриптов.
Создание рабочего листа и настройка единиц измерения для уравнений

Откройте Mathcad и создайте новый пустой лист через меню «Файл» → «Создать». Для удобства работы сохраните файл с осмысленным именем сразу после создания.
Перед вводом уравнений задайте систему единиц. В Mathcad перейдите в меню «Документ» → «Настройки документа» → вкладка «Единицы». Здесь выберите базовые единицы для длины, массы, времени и других физических величин, соответствующие вашим расчетам. Например, если уравнения описывают механические процессы, установите метр, килограмм и секунду.
Для автоматического контроля размерностей включите опцию «Проверка единиц» в тех же настройках. Это позволит Mathcad выдавать предупреждения при некорректном использовании единиц в формулах.
Для каждого используемого параметра рекомендуется задать размерность вручную. Введите переменную, затем в строке ввода нажмите правой кнопкой мыши и выберите «Добавить размерность». Это гарантирует корректное преобразование единиц при вычислениях.
После установки единиц и переменных создайте структуру рабочего листа, четко разделяя блоки с дифференциальными уравнениями, начальными условиями и расчетами. Используйте комментарии, чтобы обозначить назначение каждого блока.
Ввод первого порядка дифференциального уравнения в Mathcad

Для записи дифференциального уравнения первого порядка в Mathcad необходимо определить функцию и её производную через оператор дифференцирования. Начните с задания переменной функции, например, y(x). Затем укажите производную, используя обозначение dy/dx или встроенную команду дифференцирования diff(y(x), x).
Чтобы задать уравнение, введите равенство с левой стороны – производную функции, а справа – выражение, задающее зависимость. Например, уравнение dy/dx = x + y в Mathcad записывается как diff(y(x), x) = x + y(x).
При работе с дифференциальными уравнениями первого порядка важно обозначить переменную независимой величины (например, x) и функцию y(x) строго через аргумент x. Без этого Mathcad не распознает производную правильно.
Для численного решения уравнения используйте встроенную функцию rkfixed или odesolve, указав начальное условие в виде y(x0) = y0. Перед этим убедитесь, что уравнение записано именно в дифференциальной форме через diff(y(x), x).
Ошибки при вводе чаще всего связаны с отсутствием аргумента у функции или неправильным указанием производной. Проверяйте, что все функции имеют корректный вид y(x), а дифференцирование применяется именно к функции, а не к переменной.
Запись системы дифференциальных уравнений с использованием векторов
Для записи системы дифференциальных уравнений в Mathcad с использованием векторов необходимо определить вектор переменных и вектор производных. Создайте вектор состояния, например, x(t), где каждый элемент соответствует одной из переменных системы.
Далее задайте вектор производных dx/dt как функцию от x(t) и, при необходимости, от независимой переменной t. Например: dx/dt := f(x, t), где f – векторная функция, описывающая правые части системы.
Для ввода вектора используйте квадратные скобки с элементами через запятую: x := [x₁, x₂, ..., xₙ]. Аналогично вектору производных: dxdt := [dx₁/dt, dx₂/dt, ..., dxₙ/dt].
При формулировке уравнений запишите каждую производную через соответствующее выражение. Например, для системы из двух уравнений: dx₁/dt := x₂ + sin(t), dx₂/dt := -x₁ + cos(t). Затем объедините их в вектор: dxdt := [dx₁/dt, dx₂/dt].
Используйте оператор присваивания := для определения функций и векторов. Убедитесь, что вектор функций совпадает по размерности с вектором переменных.
Для численного решения системы с помощью встроенной функции Mathcad rkfixed или rkvariable передайте вектор производных и начальные условия в виде векторов. Например: sol := rkfixed(dxdt, t, t0, t_end, x0), где x0 – вектор начальных значений.
Таким образом, запись системы с векторами упрощает работу с несколькими уравнениями и обеспечивает удобство передачи данных в численные методы решения.
Определение начальных условий для решения уравнений в Mathcad
В Mathcad начальные условия задаются непосредственно перед определением дифференциального уравнения или системы уравнений. Они необходимы для однозначного решения задачи Коши и должны соответствовать порядку уравнения. Например, для уравнения второго порядка требуется определить значения функции и её первой производной в начальной точке.
Начальные условия задаются в формате: y(x0) = y0, где x0 – точка начала отсчёта, а y0 – значение функции в этой точке. В Mathcad синтаксис для задания начальных условий используется в виде кортежа или массива, например, {y(x0) = y0, yʹ(x0) = y1} для второго порядка.
При вводе системы уравнений важно строго следовать порядку: каждое начальное условие должно быть связано с соответствующей переменной и её производной. Ошибки в индексации или отсутствии значения приводят к сбоям при решении.
Для удобства начальные условия часто задаются как отдельные переменные перед использованием функции rkfixed или odesolve. Это упрощает изменение параметров без переписывания основного уравнения.
Использование встроенной функции для численного решения дифференциальных уравнений
Mathcad предоставляет встроенную функцию rkfixed и rkvariable для численного решения дифференциальных уравнений методом Рунге-Кутты с фиксированным и переменным шагом соответственно. Эти функции подходят для систем первого порядка и позволяют задавать начальные условия и интервал интегрирования.
- Определите функцию производной в виде
f(t, y), гдеt– независимая переменная,y– вектор зависимых переменных. В Mathcad это делается через определение пользовательской функции, например:f := (t, y) → .... - Задайте начальные условия:
t0– начальное значение времени,y0– начальный вектор состояния. - Вызовите функцию решения:
y := rkfixed(f, t0, y0, t_end, step)илиy := rkvariable(f, t0, y0, t_end, tol), гдеt_end– конечное значение времени,step– шаг интегрирования (дляrkfixed),tol– точность (дляrkvariable). - Для извлечения решения по времени создайте вектор времени
t := t0, t0+step, ..., t_endи сопоставьте значенияyдля каждогоt.
Рекомендуется выбирать начальный шаг интегрирования step не более 1% от общего интервала, а для rkvariable установить tol в пределах от 10-4 до 10-6 для баланса точности и скорости.
Для систем уравнений с несколькими переменными y должен быть вектором, а функция f возвращать вектор производных соответствующего размера. Входные и выходные данные должны строго соответствовать размерности, иначе Mathcad выдаст ошибку.
Пример вызова для системы из двух уравнений:
f := (t, y) → [y₁ - 2·y₂; 3·y₁ + y₂] y := rkfixed(f, 0, [1; 0], 10, 0.1)
После вычисления результаты можно графически отобразить с помощью стандартных инструментов Mathcad для построения графиков, сопоставляя значения t и y.
Проверка правильности записи и визуализация результатов решения
После ввода дифференциального уравнения в Mathcad необходимо убедиться в корректности его записи. Начните с анализа единиц измерения: щёлкните по выражению правой кнопкой мыши и выберите пункт «Проверить единицы». Несоответствие размерностей укажет на структурную ошибку в уравнении.
Для проверки синтаксиса активируйте отображение ошибок. Mathcad автоматически подсвечивает некорректные выражения красным. Если уравнение записано правильно, рядом с ним отобразится знак равенства, а не стрелка вычисления.
Убедитесь, что переменные и функции определены до их использования. Mathcad требует строгой последовательности. Используйте оператор определения := для задания начальных условий и функций до основного уравнения.
Для численного решения применяйте встроенную функцию odeSolve. Убедитесь, что диапазон расчёта задан через переменную, например t := 0, 0.1 .. 10, и передан в решатель.
Визуализация результата осуществляется с помощью графика: создайте ось X, укажите независимую переменную (например, t), и ось Y – соответствующее решение (например, x(t)). Выберите вставку графика из панели инструментов, затем перетащите нужные переменные на оси. Для отображения нескольких решений используйте вектор-решения и обращайтесь к ним через индексы, например sol(t)₀, sol(t)₁.
Проверьте гладкость графика: резкие скачки или разрывы могут указывать на ошибки в исходной формуле или некорректно заданные начальные условия. Для уточнения решения уменьшите шаг интегрирования или скорректируйте параметры метода в настройках odeSolve.
Для финальной верификации сравните численное решение с аналитическим, если оно известно, или выполните обратную подстановку полученной функции в исходное уравнение с использованием производной diff. Совпадение левой и правой части уравнения подтвердит корректность решения.