Maple распознаёт логарифмы по базовой функции ln(x) для натурального логарифма и log, возвращая значение 2.
Для выражений вида a*log(x) + b*log(y) рекомендуется применять правило преобразования суммы в логарифм произведения: a*ln(x) + b*ln(y) = ln(xa·yb). В Maple это записывается как expand(logcombine(a*ln(x)+b*ln(y))), что позволяет упростить дальнейшие вычисления.
При необходимости заменить основание логарифма используют формулу перехода: log[b](x) = ln(x)/ln(b). В Maple вводят convert(log[x](b), ln) или вручную ln(x)/ln(b). Это гарантирует точность при работе с иррациональными или сложными основаниями.
Чтобы вывести выражение с логарифмом в символьном виде, используйте команду print или обёртку ‘`’, например: print(`log[2](x^3 — 1)`). Это сохраняет читаемость при создании отчётов и экспортe в LaTeX.
Задание оснований логарифмов через оператор log
В Maple оператор log позволяет задавать логарифмы с любым основанием. Синтаксис:
log(b, x)– логарифм числаxпо основаниюb.- При опускании первого аргумента (
log(x)) подразумевается натуральный логарифм.
Рекомендации по применению:
- Указывать основание явно:
- Пример:
log(2, 8)вернёт3. - Для десятичного основания:
log(10, x).
- Пример:
- Объединять с упрощением:
- Команда
simplify(log(a, a^5))выдаст5. - Для выражений вида
log(b, c)*dприменяйтеcombine:combine(log(3, 9)*2, `log`)→4.
- Команда
- Работа с переменными:
- Если основание и аргумент – символы, Maple не вычисляет численно:
log(p, q)остаётся в видеlog(p, q). - Для численного результата используйте
evalf:
evalf(log(2, 7))→2.80735.
- Если основание и аргумент – символы, Maple не вычисляет численно:
- Смена оснований в формулах:
- Перевод из одного основания в другое:
log(a, x) = log(b, x) / log(b, a).
Пример:simplify(log(2, x) - log(10, x)/log(10, 2))→0.
- Перевод из одного основания в другое:
- Автоматизация в пакетах:
- Используйте
interface(log)для просмотра настроек оператора. - Подключайте пакет
Student[Calculus1]для учебных задач:
with(Student[Calculus1]): log[b](x)– альтернативный синтаксис.
- Используйте
Использование встроенных функций для натурального логарифма

В Maple для вычисления натурального логарифма применяется функция ln. Она поддерживает аргументы любого гладкого выражения: числовых констант, символических параметров, рациональных и иррациональных функций. Для числовых входных данных ln возвращает вещественное значение с плавающей точкой, например:
> ln(5);
1.6094379124341003
Чтобы получить точное символьное представление примените опцию simplify или используйте evalf для контроля точности. Рекомендуется указывать точность через Digits:
> Digits := 30:
> evalf(ln(2), 20);
0.69314718055994530942
Для логарифмирования сложных выражений комбинируйте ln с операторами упрощения: combine объединит произведение под знаком логарифма в сумму логарифмов, а expand – разложит степени:
> combine(ln(x*y));
ln(x) + ln(y)
> expand(ln(x^3));
3·ln(x)
В задачах дифференцирования и интегрирования используйте D или знак апострофа для производных и int для интегралов; Maple автоматически применит правило производной ln’(x)=1/x:
> D(ln)(x);
1/x
> int(ln(x), x);
x·ln(x) − x
Для комплексных аргументов укажите контекст assume с доменом чисел, иначе Maple добавит ветвление через I*Pi:
> assume(x > 0):
> ln(x);
ln(x)
Комбинирование логарифмов с алгебраическими выражениями
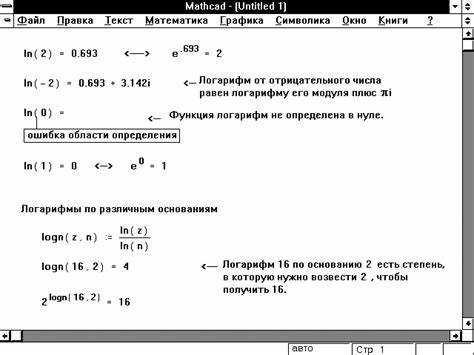
В Maple операцию объединения логарифмов удобно выполнять с помощью пакета simplify и ключевого параметра logcombine. Для выражения вида log(a) + log(b) достаточно вызвать:
simplify(log(a)+log(b), logcombine);
Результат автоматически превратится в log(a*b). Если в аргументах присутствуют дроби, например log(x/2) – log(3*y), то та же команда выдаст log(x/(6*y)).
Для выражений, где в степенях указаны переменные, например 2*log(x) – 3*log(y), перед объединением стоит привести коэффициенты к умножению внутри логарифма:
expr:=2*log(x) - 3*log(y):
expr1:=convert(expr, `*`); # логические множители
simplify(expr1, logcombine);
Maple преобразует к форме log(x^2/y^3) без ручного раскрытия степеней. Для смешанных случаев, например log(a) + 4*log(b/c), используйте последовательность:
expr:=log(a) + 4*log(b/c):
expr1:=expand(expr): # раскрывает множители
simplify(expr1, logcombine);
В сложных алгебраических подлогарифмических выражениях, включающих суммы или разности внутри аргументов (например, log(x+1) + log(x-1)), прямое объединение невозможно. В таких случаях предварительно разложите выражения на множители методом factor:
expr:=factor((x+1)*(x-1));
simplify(log(expr), logcombine);
Это даёт log(x^2-1). При работе с рациональными функциями используйте сочетание combine и simplify:
combine(log(expr), `*`);
simplify(%, logcombine);
Для контроля промежуточных шагов добавляйте опцию showsteps=true:
simplify(expr, logcombine, showsteps=true);
Таким образом, комбинация функций convert, expand, factor и simplify с параметром logcombine позволяет надёжно объединять логарифмы в любых алгебраических выражениях.
Преобразование логарифмических формул с simplify
Для упрощения логарифмических выражений в Maple используется команда simplify(expr, symbolic); с опцией symbolic, которая активирует применение логарифмических тождеств. Например,
simplify(ln(a) + ln(b), symbolic); даст ln(a*b), а simplify(2*ln(x) - ln(x^2), symbolic); упростит до 0, поскольку 2·ln(x)=ln(x^2).
Если требуется раскрыть степень внутри логарифма, используйте обратную опцию expandlog: simplify(expr, expandlog);. Например, simplify(ln(x^3), expandlog); вернёт 3·ln(x). Для комбинированного упрощения задайте список опций: simplify(expr, {symbolic, expandlog});.
При сложных формулах с разными основаниями удобно переводить все логарифмы в одно основание через функцию change_base(expr, a); до упрощения. Например,
expr := log[2](x) - log[5](y);
expr1 := change_base(expr, 10);
simplify(expr1, symbolic); выдаст результат в виде log(x)/log(2) - log(y)/log(5), после чего можно группировать с помощью simplify(..., symbolic);.
Для контроля порядка действий включайте опцию trigcomb, если формулы содержат тригонометрические и логарифмические сочетания: simplify(expr, {symbolic, trigcomb});. Это позволяет объединять выражения вида ln(sin(x)) + ln(cos(x)) в ln(sin(x)*cos(x)).
При работе с параметрами используйте assume или assuming для указания областей допустимых значений. Например,
simplify(ln(x-1) + ln(x+1) assuming x>1, symbolic); объединит в ln((x-1)*(x+1)) без ошибок.
Для пакетного применения к списку выражений используйте map(s -> simplify(s, symbolic), [expr1, expr2, expr3]);, что ускоряет обработку и сохраняет единообразие результатов.
Символьное дифференцирование логарифмических функций
Maple обеспечивает прямую работу с символическими выражениями, в том числе с логарифмами. Для получения производной логарифмической функции используется стандартная команда diff. Следует учитывать базу логарифма: по умолчанию Maple воспринимает функцию ln(x) как натуральный логарифм, а для логарифмов произвольного основания используется синтаксис log(b, x).
Для корректного дифференцирования в Maple важно заранее явно задать область определения переменных, чтобы избежать конфликтов с комплексными значениями. Рекомендуется использовать пакет assume(x, real, x>0) перед вызовом diff, если аргумент положителен по условию задачи.
| Описание | Команда Maple | Результат |
|---|---|---|
| Производная натурального логарифма | diff(ln(x), x); |
1/x |
| Производная логарифма по основанию 10 | diff(log[10](x), x); |
1/(x*ln(10)) |
| Логарифм функции от сложного аргумента | diff(ln(sin(x)^2 + 1), x); |
(2*sin(x)*cos(x))/(sin(x)^2+1) |
| Производная логарифма с произвольным основанием | diff(log(a, x^3 + 2), x); |
(3*x^2)/( (x^3+2)*ln(a) ) |
Для упрощения результата после дифференцирования рекомендуется применять функцию simplify или expand. Например, simplify(diff(log(x^2+1), x)); вернёт более компактную форму 2*x/(x^2+1). При необходимости можно использовать factor для выделения общих множителей в знаменателе или числителе.
В сложных выражениях удобно сочетать дифференцирование и автоматическое преобразование: simplify(diff(log(f(x)), x), symbolic); позволяет получить конечный результат в наиболее наглядной алгебраической форме.
Численное вычисление логарифмов с evalf
Для получения приближенных значений логарифмических выражений в Maple применяется функция evalf. Она преобразует символические результаты в числа с плавающей точкой заданной точности.
Синтаксис: evalf(expr, n), где expr – логарифмическое выражение, n – число значащих цифр (по умолчанию 10). Например, evalf(log(2), 15) возвращает значение 0.693147180559945 с точностью до 15 цифр.
Если требуется вычислить логарифм по произвольному основанию b, используйте переписывание через натуральный логарифм: evalf(log(x)/log(b), n). Пример: evalf(log(100)/log(5), 12) даст 2.86135311614678.
При работе с массивами или векторами применяйте map: map(u->evalf(log(u), 12), [1, 10, 100]) выдаст приблизительные значения 0, 2.302585093, 4.605170186.
Вложенные выражения сначала раскройте символически, затем применяйте evalf к итоговому результату. Например, evalf(exp(log(7)*3), 8) сначала вычисляет exp(3*ln(7)) символически, затем возвращает 343.000000.
При необходимости контроля точности удобно использовать Digits: изменить глобальную точность можно командой Digits:=20: перед вызовом evalf, что позволит выполнять вычисления со 20 значащими цифрами без явного указания второго аргумента.
Вопрос-ответ:
Как в Maple правильно записать логарифм двойного аргумента, например log(x*y)?
В Maple оператор log предполагает единый аргумент. Чтобы записать логарифм произведения x и y, используйте явную форму: log(x*y). Maple автоматически применит свойство логарифма произведения, если включена опция simplify. Для ручного разложения можно написать expand(log(x*y)), что даст log(x) + log(y).
Почему при вычислении log(0) в Maple возникает ошибка, и как её обойти?
Maple возвращает сообщение об ошибке, потому что логарифм нуля не определён в комплексе. Для проверки аргумента до вычисления применяйте условие: if x<>0 then log(x) else \"Не определено\" fi. Кроме того, можно определить собственную функцию-оболочку:mylog := proc(u) if u=0 then NULL else log(u) fi end proc;, что предотвратит аварийное завершение.
Как задать логарифм по произвольному основанию a, а не по e?
В Maple стандартный логарифм — натуральный. Для основания a используйте формулуlog[a](x) := log(x)/log(a).
Или сразу в вычислении: log(x)/log(a). Если требуется сделать это часто, объявите:alias(loga = u -> log(u)/log(a)); После этого можно писать loga(x).
Как в Maple упростить выражение с логарифмами, например log(x^2) − 2*log(x)?
Чтобы привести подобные члены, воспользуйтесь simplify или combine. Например:expr := log(x^2) - 2*log(x): simplify(expr);
Результатом будет 0, так как Maple понимает равенство. Команда combine(expr, 'log') попытается собрать все логарифмы в одну функцию, а expand(expr) — разложить произведения.
Можно ли в Maple вычислять логарифмы с комплексными аргументами и как отображать их разветвлённую структуру?
Да, Maple поддерживает комплексные логарифмы. По умолчанию log(z) возвращает главный аргумент: ln|z| + I*arg(z) в пределах (-π, π]. Для явного управления ветвями задайте параметр branch: interface(complexlog = true) активирует полный вывод в виде ln(z)+2*I*Pi*k, где k — целое число, обозначающее ветвь. Для конкретной ветви используйте функцию principalbranch(z, k), чтобы получить значение на ветви k.