Maple предоставляет широкий набор инструментов для создания и управления последовательностями, что позволяет эффективно работать с числовыми и символическими рядами. Для записи последовательности в Maple используют встроенную функцию seq, которая формирует элементы по заданному правилу и диапазону индексов.
Синтаксис функции seq имеет вид seq(выражение, индекс_от, индекс_до). В выражении можно использовать текущий индекс для построения каждого элемента. Например, seq(i^2, i=1..5) создаст последовательность квадратов первых пяти натуральных чисел.
Для более сложных случаев доступны вложенные последовательности и комбинирование seq с другими функциями Maple, такими как convert для преобразования результата в список или множество. Правильное использование индексов и выражений внутри seq позволяет добиться оптимальной производительности и точности при вычислении.
Создание простой числовой последовательности с помощью seq
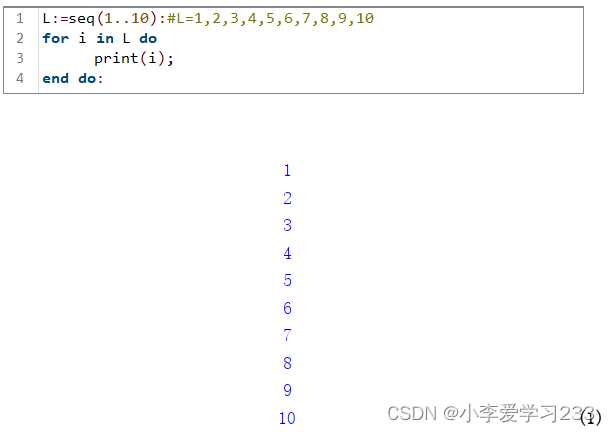
В Maple команда seq генерирует элементы последовательности по заданному правилу. Синтаксис базового вызова: seq(выражение, индекс, начало, конец). Здесь выражение – формула для вычисления каждого элемента, индекс – переменная, изменяющаяся от начала до конца.
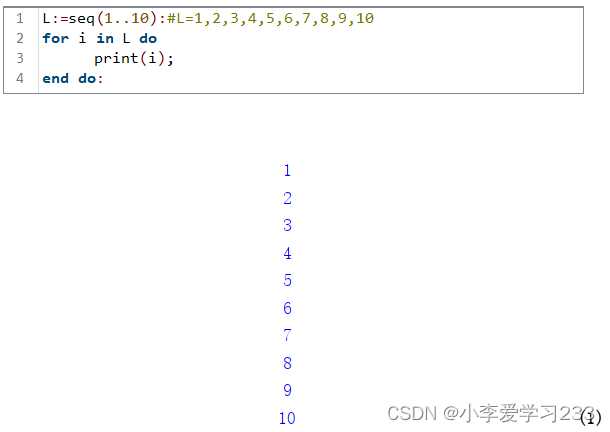
Пример создания последовательности целых чисел от 1 до 10:
seq(i, i, 1, 10);
Результат – список: 1, 2, 3, ..., 10.
Для создания арифметической прогрессии, например, с шагом 2, используют выражение с индексом:
seq(1 + 2*(i-1), i, 1, 10);
Если необходимо получить последовательность квадратов чисел от 1 до 5:
seq(i^2, i, 1, 5);
Результат: 1, 4, 9, 16, 25.
Для создания последовательности с нестандартным шагом индекса используйте конструкцию с параметром шага, например:
seq(i, i = 1 .. 10 by 2);
Здесь индекс i принимает значения 1, 3, 5, 7, 9.
Чтобы получить элементы в убывающем порядке, укажите уменьшение индекса:
seq(i, i, 10, 1, -1);
Результат: 10, 9, 8, ..., 1.
Рекомендуется использовать seq для генерации числовых списков при построении циклов и вычислении выражений, где требуется последовательное изменение параметра.
Использование генераторов для создания сложных последовательностей
В Maple генераторы представляют собой мощный инструмент для построения последовательностей с нестандартными закономерностями. Их основная особенность – ленивое вычисление элементов по мере запроса, что позволяет эффективно работать с бесконечными или очень длинными рядами.
Для создания генератора используется ключевое слово generator и оператор yield, который возвращает очередной элемент последовательности без выхода из функции. Такой подход позволяет формировать элементы по сложным алгоритмам, включая циклы с условными ветвлениями и вычислениями на предыдущих шагах.
Пример генератора для последовательности, в которой каждый следующий элемент равен сумме двух предыдущих, выглядит так:
seqGen := generator() -> do
local a := 0, b := 1, temp;
while true do
yield(a);
temp := a + b;
a := b;
b := temp;
end do;
end
Для извлечения элементов из генератора применяется функция next. Например, вызов next(seqGen()) вернёт первый элемент, повторные вызовы – последующие.
Для генерации элементов с динамическими условиями можно использовать параметры внутри генератора, что расширяет гибкость. Например, генератор, формирующий последовательность по формуле с переменным множителем, принимает этот множитель в качестве аргумента.
Рекомендуется комбинировать генераторы с функциональными конструкциями Maple, такими как map и select, чтобы дополнительно фильтровать или трансформировать последовательности без предварительного полного вычисления.
Использование генераторов особенно эффективно при работе с алгоритмами, где количество элементов заранее неизвестно или зависит от внешних условий, а также при моделировании математических процессов с неограниченным числом шагов.
Запись рекуррентных последовательностей и их вычисление
В Maple рекуррентные последовательности задаются с помощью функции rsolve или операторов рекуррентного определения. Для записи рекуррентного соотношения используется синтаксис уравнения, в котором значение последовательности выражается через предыдущие члены. Например, для последовательности Фибоначчи:
seq := a(n) = a(n-1) + a(n-2):
Необходимо указать начальные условия в виде списка:
conds := a(0) = 0, a(1) = 1:
Вычисление общего решения выполняется командой:
rsolve({seq, conds}, a(n));
Для численного вычисления значений последовательности применяют функцию seq или оператор for. Например, получить первые 10 значений можно так:
seq(rhs(rsolve({seq, conds}, a(n))), n=0..9);
Если требуется рекурсивное вычисление без нахождения общего выражения, используют функцию Vector или массив, в который поочередно записываются значения:
vals := Vector(10):
vals[1] := 0: vals[2] := 1:
for i from 3 to 10 do
vals[i] := vals[i-1] + vals[i-2]:
end do:
vals;
В Maple важно четко задавать индексацию, так как по умолчанию индексы начинаются с 1. Если начальные условия заданы с нуля, следует учитывать сдвиг индексов при вычислениях.
Для сложных рекуррентных систем допустимо использование многострочных определений и функций с несколькими аргументами. В таких случаях rsolve работает аналогично, возвращая аналитическое решение при наличии такового.
Рекомендуется всегда проверять корректность начальных условий и совместимость с рекуррентным соотношением, чтобы избежать ошибок вычисления и получить точное решение.
Определение последовательностей с условными операторами
В Maple для задания последовательностей с условными операторами применяют конструкцию seq совместно с оператором if. Это позволяет создавать элементы последовательности, меняющиеся в зависимости от индекса.
Основной синтаксис выглядит так: seq(if условие then выражение1 else выражение2 end if, индекс, начало, конец). Условие проверяется для каждого значения индекса, после чего формируется соответствующий элемент.
Например, последовательность, где чётные индексы принимают значение 0, а нечётные – индекс, задаётся так:
seq(if i mod 2 = 0 then 0 else i end if, i = 1..10).
В сложных случаях можно использовать вложенные операторы if для нескольких условий, либо оператор elif, например:
seq(if i < 5 then i^2 elif i < 8 then 2*i else 0 end if, i = 1..10).
Рекомендуется использовать оператор if в форме с явным end if, чтобы избежать синтаксических ошибок при многострочных условиях или вложениях.
Для повышения читаемости и удобства поддержки кода лучше разбивать сложные условия на отдельные логические блоки с комментариями.
Если условие зависит от нескольких переменных, рекомендуется предварительно определить вспомогательные функции или процедуры, а затем использовать их внутри seq.
Применение функций для преобразования элементов последовательности
В Maple преобразование элементов последовательности выполняется с помощью применения функций к каждому элементу. Для этого используют операторы и встроенные команды, позволяющие создавать новые последовательности на основе исходных.
Основные способы преобразования:
- map – функция, применяющая заданную функцию к каждому элементу списка или последовательности. Синтаксис:
map(f, seq), гдеf– функция,seq– исходная последовательность. - seq с функцией внутри – генерация новой последовательности с вычислением выражения для каждого индекса. Например,
seq(f(i), i=1..n)создаст последовательность из значенийf(i). - listtools:-map – расширенная версия
map, работающая с разными структурами и предоставляющая дополнительные опции.
Рекомендации по использованию:
- Для простых преобразований, таких как возведение в степень, умножение или сложение, используйте
mapс анонимной функцией или именованной процедурой. - При необходимости создавать последовательность по формуле, предпочтительнее использовать
seqс выражением, зависящим от индекса. - Если требуется изменить тип данных элементов (например, перевод из числового в строковый формат), функция преобразования должна явно это учитывать.
- Для обработки вложенных списков применяйте рекурсивные функции с
mapилиlisttools:-map, задавая глубину обхода.
Пример использования map для возведения каждого элемента последовательности [1, 2, 3, 4] в квадрат:
map(x -> x^2, [1, 2, 3, 4]);
Пример генерации последовательности, где каждый элемент равен двойному индексу:
seq(2*i, i=1..5);
Для преобразования с учетом условий можно использовать конструкции вида:
map(x -> `if`(x mod 2 = 0, x/2, x*3+1), seq(1..10));
Применение функций к элементам последовательности в Maple позволяет эффективно создавать и модифицировать данные, что облегчает последующий анализ и вычисления.
- Сохранение последовательностей в текстовый файл
Для записи последовательности в файл используйте командуfprintfилиExport.Пример:
seq := [seq(i^2, i=1..10)]; file := fopen("sequence.txt", WRITE); for i in seq do fprintf(file, "%d\n", i); end do; fclose(file);Такой подход удобен для простого хранения числовых данных.
- Экспорт в CSV формат
CSV подходит для импорта данных в табличные редакторы и статистические программы.
Используйте:
Export("sequence.csv", seq, "CSV");При экспорте списков или матриц каждая строка будет представлять собой отдельную запись с разделителем-запятой.
- Сохранение в Maple Worksheet
Для сохранения последовательности вместе с вычислениями используйте команды сохранения рабочего листа (файл .mw). Это сохраняет не только данные, но и формулы и графики.
Для отображения последовательности в удобном формате можно использовать функцию cat или преобразовать последовательность в строку:
seq := [seq(i!, i=1..7)];
str := StringTools:-Join(seq, ", ");
cat("Последовательность факториалов: ", str);
latex(seq);
Последовательность будет преобразована в математическую формулу, удобную для вставки в документы.
— Используйте экспорт в бинарные форматы или делите данные на части для оптимизации скорости записи.
— Для последовательностей с большой точностью предпочтителен текстовый формат с контролем формата чисел (например, с фиксированным количеством знаков).
— Автоматизируйте экспорт с помощью процедур, чтобы минимизировать ошибки.
Автоматизация записи последовательностей через процедуры Maple
Процедуры в Maple позволяют эффективно создавать и записывать последовательности с минимальным объемом кода. Для автоматизации используйте конструкцию proc, принимающую параметры, определяющие вид и длину последовательности.
Например, процедура для записи арифметической прогрессии задается как:
ArithmeticSeq := proc(a, d, n) local i; seq(a + (i-1)*d, i=1..n); end proc:
Здесь a – первый элемент, d – разность, n – количество элементов. Аналогично можно создать процедуру для геометрической прогрессии:
GeometricSeq := proc(a, r, n) seq(a * r^(i-1), i=1..n); end proc:
Для записи более сложных последовательностей, например, рекурсивных, используйте локальные переменные и цикл:
RecursiveSeq := proc(n) local i, s; s := [1, 1]; for i from 3 to n do s := [op(s), s[-1] + s[-2]]; od; s; end proc:
Чтобы избежать повторного вычисления значений, храните результаты в локальных структурах данных внутри процедуры. Используйте параметризацию для изменения поведения без редактирования кода.
Интегрируйте процедуры в скрипты Maple для пакетной генерации и анализа последовательностей. Автоматизация снижает количество ошибок и упрощает масштабирование вычислений.
Отладка и проверка корректности записанных последовательностей
Для проверки корректности последовательностей в Maple применяйте функцию `seq` с ключевым аргументом, например, ограничьте длину с помощью `seq(…, 1..n)` и визуально сверяйте с ожидаемыми элементами. Ошибки часто возникают из-за неверных индексов или синтаксиса, поэтому используйте команду `print` для промежуточного контроля значений.
Вычислите несколько первых элементов вручную и сравните с результатом выполнения кода. При работе с рекурсивными определениями рекомендуется проверять базовые случаи, чтобы исключить бесконечные циклы или неправильные начальные значения.
Для выявления логических ошибок используйте встроенную функцию `evalb`, которая возвращает логический результат проверки равенства элементов последовательностей. Также полезна команда `convert(…, list)`, позволяющая преобразовать последовательность в список для более удобного анализа.
Если последовательность зависит от параметров, варьируйте их значения и проверяйте устойчивость результата. Ошибки в формулах выявляются сравнением с аналитическими выражениями или стандартными функциями Maple, например, `simplify` помогает упростить выражения и выявить скрытые ошибки.
Используйте оператор `assuming` для проверки условий определения последовательности, особенно когда переменные ограничены диапазонами или типами данных. Автоматизированное тестирование с использованием цикла `for` и сравнений элементов ускорит выявление несоответствий.
Вопрос-ответ:
Как в Maple создать последовательность с использованием функции seq?
В Maple для создания последовательности применяется команда seq. Формат записи: seq(выражение, переменная, начальное_значение, конечное_значение). Например, seq(i^2, i, 1, 5) создаст последовательность квадратов чисел от 1 до 5: 1, 4, 9, 16, 25.
Можно ли сохранить результат работы seq в список или массив, и как это сделать?
Да, результат seq можно сохранить в структуру данных, например, в список или массив. Чтобы получить список, используется функция convert: convert(seq(i, i=1..5), list). Для создания массива применяется функция Array вместе с seq: Array(seq(i, i=1..5)). Это позволяет удобно работать с элементами последовательности.
Как сформировать последовательность с шагом, отличным от 1, в Maple?
В Maple в стандартной функции seq шаг по умолчанию равен 1, однако можно задать шаг через альтернативные конструкции. Например, используя генератор списка с условием, либо используя индекс с выражением для переменной. Например: seq(2*i, i=0..4) создаст последовательность 0, 2, 4, 6, 8, где шаг переменной i равен 1, а выражение умножает i на 2. Для шага, например, 0.5, можно использовать функцию seq с плавающей точкой и затем округлять или фильтровать значения.
Какие типичные ошибки встречаются при записи последовательностей в Maple, и как их избежать?
Одной из частых ошибок является неправильное указание границ индекса, например, если конечное значение меньше начального. Также ошибка — использование неподходящего типа данных для переменной индекса. Следует внимательно проверять синтаксис: скобки, двоеточия и запятые. Если результат не тот, что ожидался, стоит проверить выражение внутри seq, поскольку оно формирует каждый элемент последовательности.
Можно ли использовать вложенные последовательности в Maple, и как это реализовать?
Да, в Maple можно создавать вложенные последовательности с помощью вложенных вызовов seq. Например: seq(seq(i+j, j=1..3), i=1..2) создаст последовательность из значений для i=1 и i=2, где каждый i генерирует три значения для j. Результат будет: 2,3,4,3,4,5. Для удобства восприятия часто применяют дополнительные функции, чтобы получить матрицу или список списков.
Как в Maple записать последовательность с помощью команды seq и задать ей конкретное число элементов?
Для создания последовательности в Maple используется команда seq. Формат записи следующий: seq(выражение, переменная = начальное_значение..конечное_значение). Например, чтобы получить последовательность из десяти элементов вида 2, 4, 6, …, 20, нужно написать seq(2*i, i=1..10). Здесь переменная i принимает значения от 1 до 10, а выражение 2*i задаёт формулу для каждого элемента.
Как сохранить последовательность в виде списка или массива для дальнейшей работы в Maple?
Чтобы сохранить сгенерированную последовательность, её необходимо преобразовать в структуру данных, например, список или массив. Для преобразования в список используется функция [$seq(...)]. Например, L := [$seq(i^2, i=1..5)] создаст список из квадратов чисел от 1 до 5: [1, 4, 9, 16, 25]. Для создания массива можно применить команду Array(1..n, [список элементов]). Если требуется дальнейшая работа с отдельными элементами, список и массив удобны для индексированного доступа.