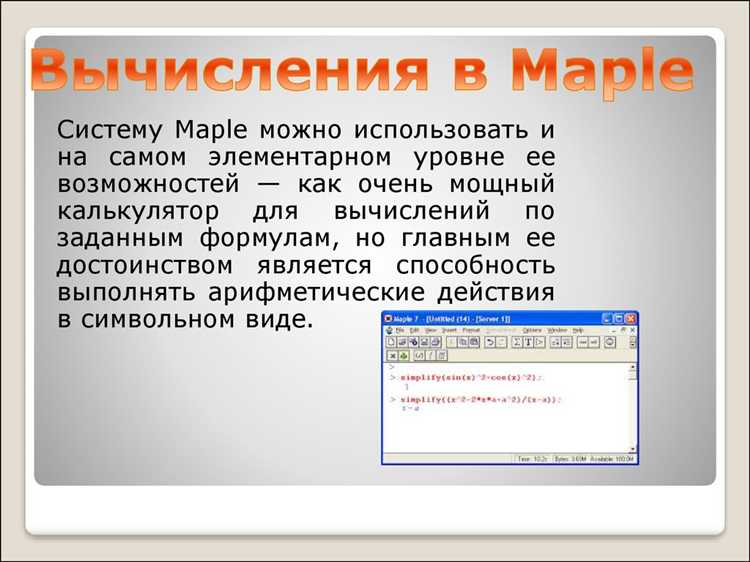
Для точного решения системы уравнений в Maple необходимо соблюдать определённый синтаксис при вводе выражений. Важно использовать символы равенства := для присваивания и = для обозначения уравнений внутри системы. Каждое уравнение записывается в виде уравнение = 0 или левая_часть = правая_часть, а все уравнения объединяются в списке или множестве через запятую и заключаются в квадратные или фигурные скобки.
Для системы с несколькими переменными нужно определить список неизвестных, которые подлежат решению, и передать их функции solve или fsolve. Пример правильного ввода: solve({x^2 + y = 4, x — y = 1}, {x, y}). Отсутствие фигурных скобок или неправильное разделение уравнений приведёт к ошибкам при вычислениях.
Maple допускает использование операторов логического И and или амперсанда & для записи условий системы, но рекомендуется придерживаться фигурных скобок с запятыми, так как это более однозначно трактуется программой. Также важно учитывать, что функции, содержащие несколько уравнений, не должны включать лишних пробелов и специальных символов, которые могут нарушить синтаксис. Соблюдение этих правил гарантирует корректное и быстрое получение решений.
Синтаксис записи уравнений в Maple
В Maple уравнения записываются с использованием оператора равенства =. Для обозначения уравнения необходимо использовать двойное равенство ==, которое отличает уравнение от присваивания.
- Правильная запись уравнения:
x^2 + 3*x == 5 - Неправильная (присваивание):
x^2 + 3*x = 5
При составлении систем уравнений каждое уравнение отделяется запятой, а вся система заключается в фигурные скобки { }. Такой формат позволяет функции solve или fsolve корректно обработать систему.
- Пример системы из двух уравнений:
{x + y == 2, x - y == 0}
Переменные не требуют предварительного объявления, но для удобства решения рекомендуется указывать список переменных явно в функции решения: solve({уравнения}, {переменные}).
Операции следует записывать согласно стандартным правилам Maple:
- Степени обозначаются символом
^, например,x^3. - Дроби можно писать через косую черту, например,
(x + 1)/(x - 1). - Математические функции –
sin(x),exp(x),ln(x)и т.д., – пишутся с обычным синтаксисом вызова.
Запрещается использовать одинарное равенство для выражения уравнений, иначе Maple воспримет это как присваивание и выведет ошибку или неверный результат.
Использование фигурных скобок для систем уравнений
В Maple система уравнений задается через фигурные скобки {}, что позволяет объединить несколько уравнений в один объект. Такой формат обязателен для функций, работающих с системами, например, solve или fsolve.
Для корректного задания системы необходимо внутри фигурных скобок перечислить уравнения через запятую, например: {x + y = 2, x — y = 0}. Maple воспринимает это как набор равенств, а не как объединение в одно сложное уравнение.
При работе с системами в фигурных скобках допускается использовать уравнения с несколькими переменными, включая параметры. Важно, чтобы каждое уравнение было логически завершенным выражением с оператором равенства =.
Фигурные скобки обеспечивают точное разграничение между уравнениями и предотвращают ошибки интерпретации, которые могут возникнуть при использовании круглых скобок или списков []. Например, выражение solve({x^2 + y^2 = 1, x — y = 0}) корректно распознает систему, а solve([x^2 + y^2 = 1, x — y = 0]) может привести к ошибкам.
При составлении больших систем рекомендуется структурировать их внутри фигурных скобок, а не объединять уравнения через логические операторы, чтобы упростить последующий анализ и решение.
Обозначение переменных и параметров в системе
В Maple переменные системы уравнений задаются как символы, например, x, y, z. Они должны совпадать с теми, которые встречаются в уравнениях, иначе система не распознается корректно. Параметры в уравнениях рекомендуется обозначать отдельными символами, отличными от переменных, чтобы избежать конфликтов при решении.
При объявлении системы используйте список переменных как второй аргумент функции solve или fsolve, например, solve({u+v=1, u-v=2}, {u, v}). Параметры не включайте в этот список, их значения задавайте отдельно или оставляйте неопределенными для последующего анализа.
Не используйте числовые индексы в именах переменных (x1, x2), если планируется обрабатывать систему векторно. В таких случаях предпочтительно применять списки или массивы, например, x[1], x[2], что обеспечивает корректную работу встроенных функций Maple.
Для параметров, которые принимают конкретные значения, используйте оператор присваивания перед решением системы, например, a := 3. Это исключит неоднозначности при интерпретации уравнений и позволит получить численное решение.
Избегайте одновременного использования одинаковых имен для переменных и параметров, чтобы предотвратить перезапись значений и ошибки в вычислениях. В случае необходимости параметр можно обозначить через заглавные буквы, например, A, B, а переменные – через строчные.
Запись линейных и нелинейных уравнений
В Maple система уравнений задаётся списком или множеством выражений, каждое из которых должно быть приведено к виду равенства. Линейные уравнения записываются с использованием стандартного синтаксиса, например:
{2*x + 3*y = 5, 4*x - y = 1}
При этом важно отделять уравнения запятыми и использовать фигурные скобки для объединения в систему. Переменные указываются явно, без дополнительных символов. В случае с линейными уравнениями коэффициенты должны быть числовыми или параметрическими константами, Maple корректно воспринимает их без дополнительных преобразований.
Для нелинейных уравнений можно использовать аналогичный формат, но с учётом функций и степеней. Например, система:
{x^2 + y = 3, sin(x) - y^2 = 0}
записывается так же, без изменений в структуре, что позволяет однозначно интерпретировать уравнения при решении. Важно соблюдать синтаксис функций Maple: sin(x), exp(y), ln(z) и т.д.
Если уравнения содержат параметры, их нужно определять заранее или включать в систему в явном виде. Например:
{a*x + y = b, x^2 + y^2 = c}
где a, b, c – параметры, значение которых можно задавать отдельно через оператор assume или в момент вызова решателя.
При записи системы избегайте использования выражений, не являющихся равенствами, например, выражений с двойным равенством (== в смысле логического сравнения) или неявных функций без равенства. Правильный формат – это уравнения, каждое из которых имеет слева и справа чётко выраженную часть.
Передача системы уравнений в функцию solve
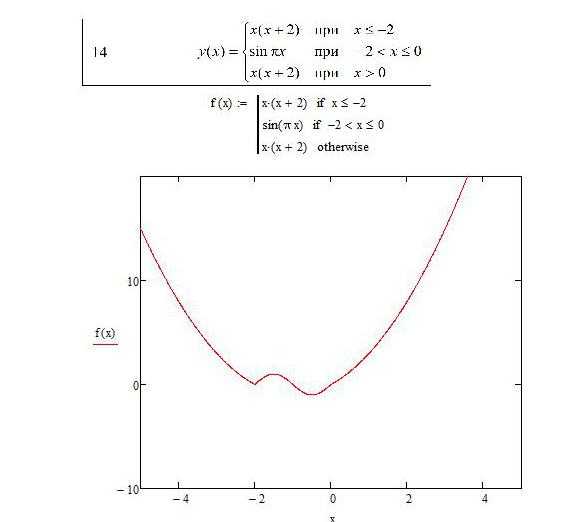
В Maple функция solve принимает систему уравнений в виде списка или множества. Для однородных уравнений запись должна содержать каждое уравнение с оператором равенства =, например: {x + y = 3, 2*x - y = 5}. Рекомендуется использовать фигурные скобки для группировки, так как это явно указывает Maple, что передается именно система, а не отдельное выражение.
Переменные, по которым производится решение, следует передавать вторым аргументом функции solve в виде списка: [x, y]. Это исключает неоднозначность, особенно при наличии параметров или дополнительных неизвестных.
Если система содержит нелинейные уравнения, синтаксис не меняется, но для удобства проверки решений рекомендуется использовать allvalues для получения всех корней. Для линейных систем достаточно базового вызова с системой в фигурных скобках и списком переменных.
Пример корректного вызова:
solve({x^2 + y = 4, x - y = 1}, [x, y]);
Важно: передавать уравнения в формате выражений без явного оператора равенства (:=) нельзя, иначе Maple воспримет это как присваивание, что приведет к ошибке.
Для систем с большим числом уравнений удобно формировать список уравнений программно и передавать в solve целиком. Использование списков и множеств с операторами равенства обеспечивает точное определение системы и корректный разбор Maple.
Работа с параметрическими системами уравнений
В Maple для решения систем уравнений с параметрами рекомендуется использовать структурированный ввод, где параметры явно обозначены как символы без присвоенных значений. Например, система с параметрами a и b записывается так: {eq1, eq2, ...}, где eq1 := x + a*y = b.
Для решения параметрических систем следует применять команду solve или fsolve с указанием параметров в списке неизвестных. Если требуется анализ решений при различных значениях параметров, целесообразно использовать оператор subs для подстановки конкретных значений после получения общего решения.
Важный момент – указывать условия на параметры, особенно если от них зависит тип решения (например, чтобы избежать деления на ноль). Это реализуется через добавление неравенств в команду solve с использованием опции assuming.
Для упрощения работы с параметрическими системами полезна функция parameters, которая позволяет получить список параметров, встречающихся в системе, и избежать конфликтов с переменными.
При численном решении параметрических систем с помощью fsolve рекомендуется фиксировать параметры до вызова функции, чтобы исключить неоднозначность интерпретации и обеспечить устойчивость вычислений.
Для построения графиков решений при изменении параметров используйте циклы с подстановкой разных значений параметров и сохранением результатов в списках или массивах. Это позволит эффективно визуализировать зависимость решений от параметров.
Проверка правильности записи системы в Maple
Для убедительной проверки корректности записи системы уравнений в Maple следует использовать функцию is() или попытаться найти решение с помощью solve(). Важно проверить, что все переменные определены и не содержат опечаток. Система должна быть задана в формате списка, например: sys := {eq1, eq2, eq3};.
После ввода системы выполните команду indets(sys) для выявления всех использованных переменных и констант. Если функция возвращает лишние символы, это указывает на ошибки в записи.
Используйте lhs(eq) - rhs(eq) для каждой записи, чтобы убедиться, что уравнения корректно оформлены в виде равенств. Ошибкой считается отсутствие оператора равенства или неправильное его расположение.
Команда evalc(simplify(subs(vars, eq))) применена к каждому уравнению помогает выявить синтаксические ошибки и логические несоответствия, если подставить тестовые значения для переменных.
При решении системы solve(sys, vars) в случае пустого результата или сообщения об ошибке следует проверить соответствие количества уравнений и переменных, а также типы уравнений – они должны быть алгебраическими или дифференциальными, в зависимости от задачи.
Для больших систем рекомендуется использовать algsys := convert(sys, list); и пройтись по каждому уравнению отдельно, чтобы локализовать ошибки.
Вопрос-ответ:
Как правильно задать систему уравнений в Maple, если в ней несколько переменных?
Для записи системы с несколькими переменными в Maple нужно использовать фигурные скобки, внутри которых перечислить уравнения через запятую. Например, система с уравнениями для переменных x и y записывается так: {x + y = 2, x — y = 0}. Это помогает программе корректно понять, что перед ней именно система, а не отдельные выражения.
Можно ли в Maple записать систему уравнений с параметрами и как это сделать?
Да, в Maple возможно указать параметры внутри системы уравнений. Параметры можно обозначить как обычные переменные и включить в уравнения. Главное — убедиться, что при решении вы явно указываете, какие переменные надо искать, а какие считать заданными параметрами. Например, если система содержит параметр a, то уравнения записываются как {a*x + y = 3, x — a*y = 1}. При вызове команды решения следует указать переменные, например solve({…}, {x, y}), чтобы Maple не пытался решать относительно параметра a.
Как в Maple задать систему уравнений для последующего численного решения?
Для численного решения системы сначала необходимо корректно записать уравнения в виде множества или списка, а затем использовать функцию fsolve вместо solve. Например, если система записана как {x^2 + y^2 = 1, x — y = 0}, то для численного решения используется вызов fsolve({x^2 + y^2 = 1, x — y = 0}, {x, y}). Это позволит найти численные приближённые значения переменных. При этом важно задать переменные, по которым идет поиск, и при необходимости указать диапазон значений для решения.
В чем ошибка, если Maple не распознает систему уравнений, и как ее исправить?
Часто проблема возникает из-за неправильного синтаксиса — например, использование круглых скобок вместо фигурных, отсутствие запятых между уравнениями или неправильное обозначение равенства (нужно использовать знак =, а не :=). Для корректного распознавания системы следует применять фигурные скобки вокруг всех уравнений, разделять их запятыми и использовать знак равенства (=) для выражения уравнений. Также стоит проверить, что переменные в системе объявлены или используются последовательно.