Как можно решить нелинейное уравнение в mathcad

Нелинейные уравнения встречаются во множестве инженерных и научных задач: от моделирования сложных физических процессов до вычисления параметров экономических моделей. В отличие от линейных, они могут содержать экспоненты, логарифмы, тригонометрические функции и другие выражения, что делает их решение значительно сложнее. Mathcad предоставляет мощный инструментарий для поиска решений таких уравнений, обеспечивая наглядность вычислений и удобство работы с аналитическими и численными методами.

В Mathcad доступны несколько методов решения нелинейных уравнений, включая численные подходы, такие как метод Ньютона-Рафсона и метод секущих, а также аналитические решения при наличии явных формул. Преимуществом использования Mathcad является возможность легко переключаться между методами и моментально видеть результат в графической и численной форме. Это особенно важно при решении уравнений с множеством корней или сложной структурой функций.

Одним из ключевых инструментов Mathcad является оператор root, позволяющий быстро находить корни уравнений при указании начального приближения. В сочетании с интерактивными графиками можно не только вычислить корни, но и визуализировать процесс сходимости метода. Это упрощает анализ поведения функции и поиск наиболее оптимального решения.

Далее в статье будут рассмотрены основные методы решения нелинейных уравнений в Mathcad, детально разобраны примеры с пошаговыми инструкциями и рекомендациями по улучшению сходимости численных алгоритмов.

Пошаговое решение нелинейных уравнений с использованием функции Find в Mathcad

Функция Find в Mathcad позволяет находить решения нелинейных уравнений или систем уравнений численными методами. Для корректного использования необходимо задать начальные приближения, поскольку метод основан на итеративных вычислениях, зависящих от исходной точки поиска.

Рассмотрим пошаговое решение на примере уравнения:

\[x^3 — 5x + 3 = 0\]

Шаг 1: Определение переменной и начального приближения.

В Mathcad создается переменная x и задается начальное приближение, например, x := 1. Это значение влияет на сходимость и выбор корня, поэтому его стоит подбирать, опираясь на график функции или аналитический анализ.

Шаг 2: Определение уравнения.

Необходимо ввести уравнение в Mathcad в виде выражения:

\[f(x) := x^3 — 5x + 3\]

Шаг 3: Применение функции Find.

Для поиска решения используется следующая конструкция:

\[x := Find(f(x))\]

Mathcad выполняет численный поиск, начиная с заданного приближения, и вычисляет значение x, удовлетворяющее уравнению.

Шаг 4: Проверка решения.

Для проверки можно подставить найденное значение обратно в уравнение:

\[f(x) = 0\]

Если результат близок к нулю (погрешность зависит от настроек точности в Mathcad), решение корректно.

Шаг 5: Поиск дополнительных корней (если необходимо).

Для поиска других корней измените начальное приближение и повторите вычисления. Например, установите x := -2 и снова вызовите Find(f(x)).

Функция Find удобна для быстрого нахождения корней, но требует внимательного выбора начальных значений для успешной сходимости.

Метод Ньютона в Mathcad: реализация и особенности применения

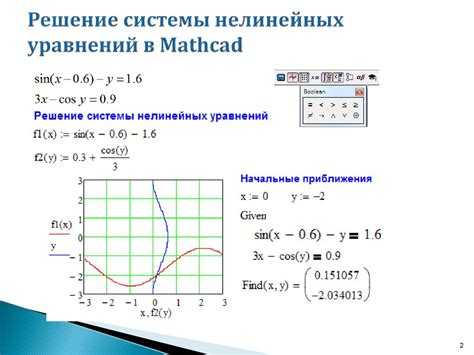
Для решения уравнения вида f(x) = 0 в Mathcad необходимо задать функцию f(x) и её производную f'(x). Это можно выполнить с помощью стандартных операторов дифференцирования или вручную, если выражение достаточно сложное. Начальное приближение x₀ выбирается на основе графического анализа или экспертных оценок, чтобы избежать сходимости к неподходящим корням или дивергенции.

Итерационная формула метода Ньютона:

xₙ₊₁ = xₙ — f(xₙ) / f'(xₙ)

В Mathcad последовательные значения xₙ можно вычислять с использованием оператора «Given… Find». Для этого задаётся начальное приближение, функция, её производная и критерий остановки итераций, например, по величине изменения решения или значению функции на текущем шаге. Также можно использовать блок «solve block» для автоматического вычисления при заданных условиях.

Особенности применения метода Ньютона в Mathcad:

1. Скорость сходимости. Метод обладает квадратичной сходимостью при условии, что начальное приближение достаточно близко к искомому корню.

2. Чувствительность к начальному приближению. Некорректный выбор x₀ может привести к дивергенции или нахождению другого корня.

3. Проблемы на точках экстремума. Если производная f'(x) обращается в ноль в процессе итераций, метод может потерять сходимость.

4. Комплексные корни. Mathcad позволяет использовать метод Ньютона для поиска комплексных корней, если начальное приближение задано в комплексной форме.

5. Графический анализ. Визуализация функции и её касательных в Mathcad помогает наглядно оценить процесс сходимости и скорректировать начальное приближение при необходимости.

Метод Ньютона в Mathcad удобен для быстрого и наглядного поиска решений нелинейных уравнений, однако требует внимательного выбора начальных данных и понимания поведения функции вблизи предполагаемого корня.

Применение метода секущих для решения уравнений в Mathcad

Метод секущих представляет собой численный способ нахождения корня нелинейного уравнения вида f(x) = 0. В отличие от метода Ньютона, он не требует вычисления производной функции, что делает его удобным для функций со сложной аналитической формой. В Mathcad реализация метода секущих достигается с помощью итеративных вычислений с заданием начальных приближений.

Для применения метода секущих в Mathcad необходимо:

1. Определить уравнение f(x) = 0. Например:

f(x) := x^3 — 4x + 1

2. Задать два начальных приближения x0 и x1, которые находятся вблизи предполагаемого корня. Например:

x0 := 0

x1 := 1

3. Ввести итеративную формулу метода секущих:

x(n+1) := x(n) — f(x(n)) * (x(n) — x(n-1)) / (f(x(n)) — f(x(n-1)))

4. Настроить критерий остановки. В Mathcad это можно реализовать с помощью цикла, например, до тех пор, пока |x(n+1) — x(n)| < ε, где ε – заданная точность.

x_root := x(n+1)

Метод секущих в Mathcad демонстрирует быструю сходимость при удачном выборе начальных приближений. Однако, если точки x0 и x1 лежат слишком далеко от корня или функция имеет разрывы, метод может не сойтись. В таких случаях следует пересмотреть начальные значения или воспользоваться другими методами, например, методом бисекции.

Использование функции Root в Mathcad для поиска корней уравнений

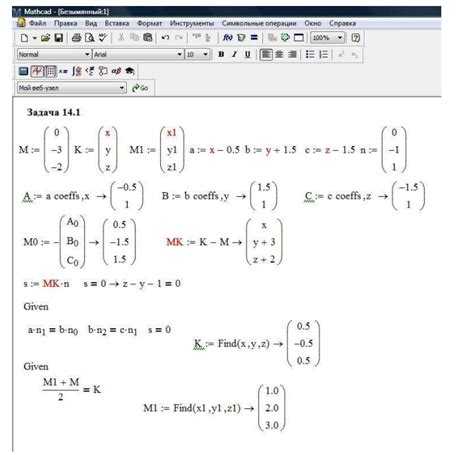
Функция Root в Mathcad предназначена для нахождения корней нелинейных уравнений. Она позволяет находить такие значения переменной, при которых выражение обращается в ноль. Синтаксис функции следующий:

Root(f(x), x, x₀)

Здесь:

f(x) – нелинейная функция, для которой ищется корень;
x – переменная уравнения;
x₀ – начальное приближение (предполагаемое значение корня).

Mathcad использует метод Ньютона для уточнения значения корня, начиная с указанного приближения x₀. Чем ближе это значение к реальному корню, тем быстрее будет достигнуто решение. Если функция имеет несколько корней, результат зависит от выбора начального приближения.

Пример использования функции:

f(x) := x^3 - 4x + 1
x₀ := 1
x_root := Root(f(x), x, x₀)

В этом случае Mathcad найдет корень уравнения x³ — 4x + 1 = 0, начиная поиск с точки x = 1.

Для повышения точности можно изменить начальное приближение или преобразовать уравнение. Например, при наличии нескольких корней можно попробовать разные значения x₀, чтобы найти другие решения.

Если корень не найден, Mathcad выдаст сообщение об ошибке. Это может означать неправильный выбор начального приближения или отсутствие корней в заданной области. В таких случаях рекомендуется построить график функции для оценки положения корней.

Решение систем нелинейных уравнений в Mathcad: подходы и примеры

Given…Find: используется для поиска численных решений системы уравнений. Mathcad автоматически применяет численные методы, такие как метод Ньютона или модифицированные итерационные алгоритмы.
Minimize/Maximize: позволяет решать задачи оптимизации, которые могут включать условия в виде нелинейных уравнений. Применяется, если необходимо найти экстремумы при заданных ограничениях.

Для решения системы необходимо:

Определить уравнения в аналитическом виде.
Использовать блок Given для задания условий.
Вызвать функцию Find(x, y, ...), передав переменные системы.
Mathcad вернёт численные значения переменных, удовлетворяющие всем уравнениям.

Пример:

Given
x^2 + y^2 = 25
x - y = 5
Find(x, y)

После выполнения расчёта Mathcad вернёт значения x = 5 и y = 0, удовлетворяющие системе. При изменении условий или добавлении уравнений Mathcad автоматически пересчитает значения.

Если решение не существует или система противоречива, Mathcad отобразит сообщение об ошибке. Для более сложных систем рекомендуется задавать начальные приближения с помощью оператора Given:

Given
x^2 + y^2 = 25
x - y = 5
x = 7  // начальное приближение
y = 2  // начальное приближение
Find(x, y)

Использование начальных значений ускоряет сходимость и повышает вероятность нахождения корней в области интереса. Это особенно полезно при наличии нескольких решений или сложной нелинейной зависимости.

Графический метод нахождения решений в Mathcad: визуализация и анализ

Графический метод в Mathcad заключается в построении графиков функции и визуальном определении точек пересечения с осью абсцисс, что соответствует корням уравнения. Для этого необходимо задать уравнение как функцию, например, f(x):= x^3 - 2x - 5, и построить ее график в интервале, где ожидаются решения.

Для точной визуализации рекомендуется использовать команду plot с тщательно выбранным диапазоном по оси X, например, от -3 до 3, и достаточным числом точек дискретизации (не менее 200) для плавности кривой. Это обеспечивает более точное определение приблизительных значений корней.

После построения графика можно визуально оценить количество и расположение решений. Для их уточнения применяется команда root, где начальное приближение берется исходя из графического анализа. Mathcad позволяет интерактивно изменять параметры графика, например масштаб и сетку, что облегчает анализ поведения функции около корней.

Важный аспект – проверка устойчивости решения. Изучение производной функции в точках пересечения (через команду diff) помогает определить, насколько корень устойчив к изменению параметров. Если производная близка к нулю, решение может быть чувствительным, что требует дополнительного численного анализа.

Графический метод полезен для начального поиска решений и выявления особенностей функции, таких как экстремумы и точки перегиба, влияющие на количество корней. При работе с системой нелинейных уравнений строятся графики всех функций одновременно, и пересечения их кривых указывают на общие решения.

Проверка и интерпретация полученных решений в Mathcad

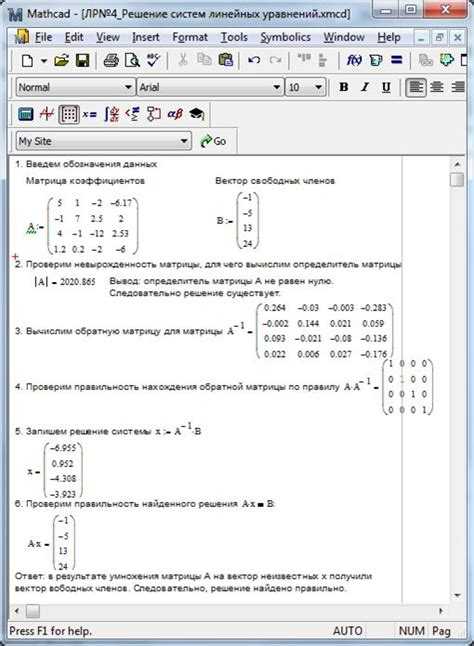
После получения корней нелинейного уравнения в Mathcad необходимо подтвердить их корректность и оценить качество решения. Первый шаг – подстановка найденных значений в исходное уравнение с помощью выражения, вычисляющего остаток (разницу между левой и правой частями). Если абсолютное значение остатка превышает 10^-6, результат требует дополнительной проверки или уточнения параметров численного метода.

Для визуальной оценки целесообразно построить график функции в окрестности найденного решения. Если график пересекает ось абсцисс строго в точке корня, это подтверждает решение. При наличии нескольких корней использование Mathcad функции root позволяет проверить устойчивость решения при различных начальных приближениях.

Интерпретация результатов включает анализ контекста задачи и проверку на физическую или математическую приемлемость корней. Например, отрицательные значения, если они невозможны по условию, должны быть исключены. В случае сложных уравнений рекомендуется проводить чувствительный анализ, изменяя параметры и фиксируя вариации решений.

Для автоматизации проверки в Mathcad можно задать массив решений и с помощью оператора vector проверить функцию на каждом элементе, что ускоряет анализ множества корней. При необходимости следует использовать встроенные функции для вычисления производной и оценивать поведение функции в окрестности решения, что помогает выявить кратные корни или точки перегиба.

Автоматизация поиска решений в Mathcad с использованием программирования

Для автоматизации поиска решений нелинейных уравнений в Mathcad применяется встроенный язык программирования с возможностью создания пользовательских функций и циклов. Такой подход позволяет ускорить вычисления и повысить точность результатов, минимизируя ручные ошибки.

Основные шаги для автоматизации:

Определение функции – задайте уравнение или систему в виде функции с входными параметрами.
Выбор метода решения – используйте встроенные функции Mathcad, например, root или solve, либо реализуйте численные методы (метод Ньютона, бисекции) программно.
Написание управляющего цикла – создайте цикл с условием остановки по достижению заданной точности или по количеству итераций.
Обработка исключений – добавьте проверку на сходимость и условия выхода из цикла для предотвращения зацикливания.

Пример программного кода на Mathcad для решения уравнения методом Ньютона:

NewtonMethod(x₀, ε, maxIter) :=
x := x₀
for i in 1..maxIter do
f := yourFunction(x)
df := derivative(yourFunction)(x)
if abs(f) < ε then
return x
x := x - f / df
return "Не сошлось"

Рекомендации по эффективной автоматизации:

Используйте в функциях параметризацию, чтобы менять уравнения без переписывания кода.
Внедряйте логирование итераций для диагностики проблем с сходимостью.
Оптимизируйте вычисления, избегая повторных вычислений одинаковых выражений.
При решении систем уравнений применяйте векторные и матричные операции Mathcad для повышения производительности.

Автоматизация позволяет интегрировать поиск решений в сложные вычислительные проекты, где требуется многократный анализ при изменении параметров, что значительно расширяет возможности использования Mathcad в инженерных и научных задачах.

Вопрос-ответ:

Какие основные методы решения нелинейных уравнений доступны в Mathcad?

В Mathcad можно применять несколько способов для решения нелинейных уравнений. Среди них наиболее распространены метод Ньютона (касательных), метод простых итераций и встроенные численные функции, такие как root или find. Каждый метод имеет свои особенности: например, метод Ньютона требует производной функции и быстрее сходится при хорошем приближении, а метод простых итераций проще, но может требовать больше шагов. Также в Mathcad можно решать системы уравнений и работать с уравнениями с параметрами.

Как правильно задавать уравнение для решения в Mathcad, если оно содержит несколько переменных?

Если уравнение включает несколько неизвестных, необходимо либо зафиксировать значения всех переменных, кроме одной, либо использовать встроенные функции для систем уравнений. Например, функция root позволяет искать корни с начальным приближением для каждой переменной. В Mathcad также удобно задавать систему уравнений с помощью векторного или матричного представления, что упрощает работу с несколькими переменными и позволяет получить решение сразу для всего набора уравнений.

Какие ошибки часто встречаются при решении нелинейных уравнений в Mathcad и как их избежать?

Распространенные ошибки связаны с неправильным выбором начального приближения, что может привести к отсутствию сходимости или нахождению ложного корня. Также встречается неправильный ввод функции или опечатки, из-за которых Mathcad не может корректно вычислить выражение. Чтобы этого избежать, важно тщательно проверять исходные данные, использовать адекватные приближения и, при необходимости, графически оценивать поведение функции перед запуском численных методов. Дополнительно полезно отслеживать предупреждения и сообщения об ошибках, которые выдает программа.

Можно ли решать нелинейные уравнения с параметрами и как отследить влияние параметров на решения в Mathcad?

Да, Mathcad позволяет решать уравнения, содержащие параметры. Для этого параметры задаются как переменные с фиксированными значениями, которые можно изменять. После нахождения решения для одного набора параметров можно быстро поменять их значения и получить новое решение. Чтобы отследить, как параметры влияют на корни уравнения, удобно использовать таблицы значений или графики, которые отображают зависимости корней от параметров. Такой подход помогает анализировать поведение уравнения при различных условиях.

Какие примеры задач можно решить с помощью нелинейных уравнений в Mathcad и какие методы при этом подходят лучше всего?

С помощью Mathcad можно решать широкий круг задач: от нахождения точек пересечения кривых до расчетов устойчивости конструкций, задач химической кинетики и экономических моделей. Для задач с гладкими функциями и доступными производными хорошо подходит метод Ньютона, так как он быстро сходится. Если производные сложно найти или функция задана неявно, удобнее применять метод простых итераций или встроенные численные алгоритмы root и find. Важно подбирать метод в зависимости от специфики задачи и особенностей уравнения.

Какие методы решения нелинейных уравнений доступны в Mathcad и в каких случаях каждый из них лучше применять?

В Mathcad предусмотрено несколько способов для решения нелинейных уравнений, включая метод касательных (Ньютона), метод простой итерации, метод бисекции и секущих. Метод Ньютона обычно используют при наличии производной функции и достаточно близком начальном приближении к корню, поскольку он обеспечивает быструю сходимость. Метод бисекции более надежен и прост, но требует задания интервала, где функция меняет знак. Метод простой итерации подходит, если уравнение можно преобразовать к виду, удобному для итерационного процесса, но он может сходиться медленно. Метод секущих похож на метод Ньютона, но не требует вычисления производной, что полезно, если производная трудна для нахождения. Выбор метода зависит от особенностей задачи, гладкости функции и доступности производной.