MATLAB предоставляет мощный и лаконичный синтаксис для создания матриц различных размеров и типов. Однострочное задание матрицы с помощью квадратных скобок [] позволяет быстро определить как векторы, так и многомерные массивы. Пробелы или запятые используются для разделения элементов по строке, а точка с запятой – для перехода на следующую строку.
Для генерации числовых последовательностей часто применяются выражения вида start:step:end. Например, 1:2:9 создаст строковый вектор [1 3 5 7 9]. Если шаг не указан, он считается равным единице. Функция linspace(a, b, n) используется для получения равномерно распределённых значений между a и b в количестве n штук.
Создание нулевых, единичных и случайных матриц осуществляется с помощью функций zeros, ones, rand и randn. Например, вызов zeros(3, 4) создаёт матрицу 3×4, заполненную нулями. Аналогичным образом, ones(2) создаёт квадратную 2×2 матрицу из единиц, а randn(5) – массив из нормальных случайных величин размером 5×5.
Для сборки сложных структур используется функция cat, а также вертикальное и горизонтальное объединение с помощью [A; B] и [A, B]. Чтобы задать диагональную матрицу, применяется diag, а для единичной матрицы – eye. Такие подходы позволяют гибко управлять структурой данных и подготавливать их к последующей обработке.
Инициализация матрицы с заданными значениями
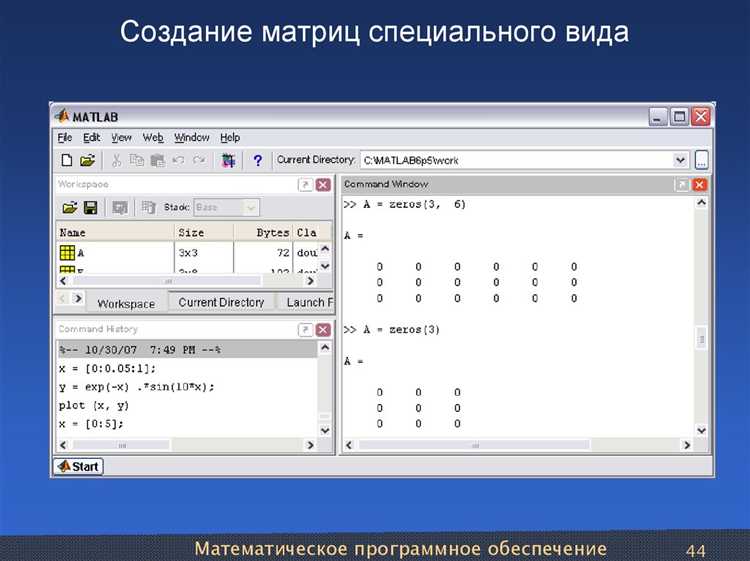
В MATLAB матрицу с фиксированными значениями удобно создавать с помощью квадратных скобок. Элементы в строке разделяются пробелами или запятыми, строки – точкой с запятой. Например, A = [1 2 3; 4 5 6; 7 8 9] формирует матрицу 3×3.
Для создания строковых матриц используют кавычки: S = ["a" "b"; "c" "d"]. Все элементы должны иметь одинаковую длину либо использовать char-массивы с выравниванием: C = ['cat'; 'dog'].
Для чисел с плавающей точкой можно задавать значения с экспонентой: B = [1e-3, 2.5, -4e2]. Комплексные числа вводятся через i или j: Z = [1+2i, 3-4j].
Для предопределения структуры матрицы можно использовать функции zeros, ones, eye, затем заменить нужные элементы вручную: M = zeros(3); M(1,1) = 5.
Для инициализации на основе выражений используйте двоеточие или linspace: X = 1:0.5:3 создаёт строку с шагом 0.5, L = linspace(0, 1, 5) – вектор из пяти равномерно распределённых значений от 0 до 1.
Используйте фигурные скобки для ячеек: C = {1, 'text'; rand(2), pi}. Такой способ подходит для хранения разнотипных данных в одной структуре.
Создание нулевых, единичных и случайных матриц
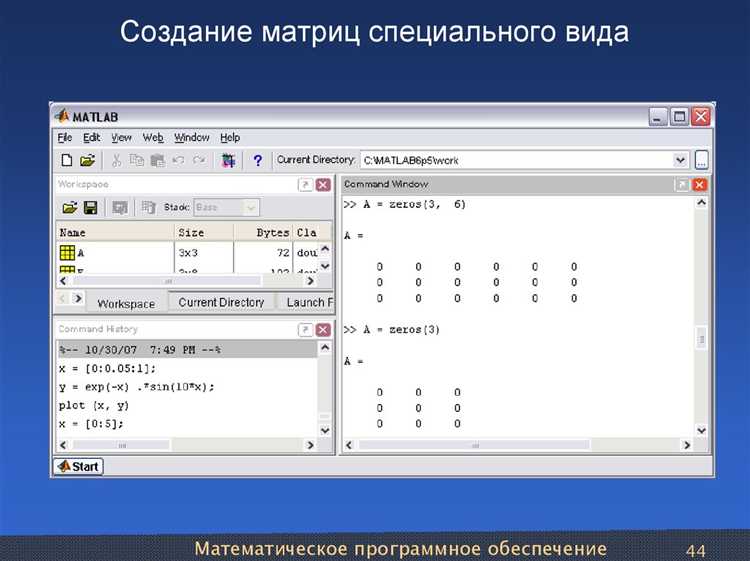
Для генерации матриц с предопределённой структурой в MATLAB используются встроенные функции zeros, ones и rand. Эти функции позволяют создавать массивы нужного размера без необходимости вручную заполнять значения.
Нулевая матрица создаётся с помощью команды zeros. Синтаксис zeros(m, n) формирует матрицу размером m на n, где все элементы равны нулю. Для трёхмерных массивов используется zeros(m, n, k). Чтобы создать вектор, достаточно одного аргумента: zeros(n, 1) – столбец, zeros(1, n) – строка.
Единичная матрица генерируется функцией ones. По структуре она аналогична zeros. Например, ones(3) создаёт квадратную матрицу 3×3, полностью заполненную единицами. Применяется для инициализации весов в нейросетях и других случаев, где требуется одинаковое начальное значение.
Случайная матрица создаётся функцией rand, возвращающей значения с равномерным распределением от 0 до 1. Пример: rand(4, 2) – матрица 4×2 со случайными числами. Для получения значений в другом диапазоне используется линейное преобразование: a + (b - a) * rand(m, n), где a и b – границы диапазона. Чтобы зафиксировать генерацию для повторного использования, применяют rng(seed).
Использование этих функций позволяет точно контролировать размер и содержимое создаваемых матриц, минимизируя вероятность ошибок при инициализации данных в вычислительных задачах.
Использование функций linspace и colon для генерации строк

В MATLAB функции linspace и оператор : применяются для создания строк с равномерным шагом, но отличаются по принципу работы и областям применения.
linspace(a, b, n)– генерирует строку изnэлементов, равномерно распределённых отaдоbвключительно. Применяется, когда нужно задать точное количество точек.a:h:b– создает строку отaдоbс шагомh. Используется, когда важен шаг между значениями, а не их количество.
Примеры:
linspace(0, 1, 5)возвращает[0 0.25 0.5 0.75 1]0:0.25:1возвращает то же самое, но результат зависит от точности вычислений, особенно при дробных шагах
Рекомендации:
- Для численного моделирования с фиксированным числом точек используйте
linspace– он гарантирует включение правой границы. - Для циклов и дискретных шагов применяйте
:, особенно при работе с целыми числами. - Избегайте
:с дробными шагами, если требуется высокая точность – используйтеlinspaceвместо этого. - При построении графиков, где требуется равномерное распределение, предпочтительнее
linspace, чтобы избежать накопления ошибки округления.
Выбор между этими инструментами зависит от задачи: linspace – для количества, : – для шага.
Формирование матриц с помощью функции reshape
Функция reshape в MATLAB используется для изменения размерности массива без изменения его данных. Исходный массив заполняется по столбцам, и новая матрица также формируется по столбцам.
Синтаксис: B = reshape(A, m, n) преобразует массив A в матрицу размером m × n, при условии, что numel(A) == m*n.
Пример: пусть A = 1:12; – строковый вектор. Команда reshape(A, 3, 4) вернёт матрицу:
| 1 | 4 | 7 | 10 |
| 2 | 5 | 8 | 11 |
| 3 | 6 | 9 | 12 |
Для многомерных массивов допустимо указание более двух размеров: reshape(A, d1, d2, ..., dn). Например, reshape(1:8, 2, 2, 2) создаёт трёхмерный массив.
Если размер не известен заранее, один из аргументов можно задать как []. MATLAB сам вычислит соответствующее значение. Пример: reshape(1:10, [], 5) создаёт матрицу 2 × 5.
При работе с reshape важно учитывать порядок элементов. Если требуется построчная перестановка, необходимо использовать транспонирование перед или после reshape.
Не допускается использование reshape для изменения общего количества элементов. Нарушение этого условия вызывает ошибку выполнения.
Добавление строк и столбцов к существующей матрице
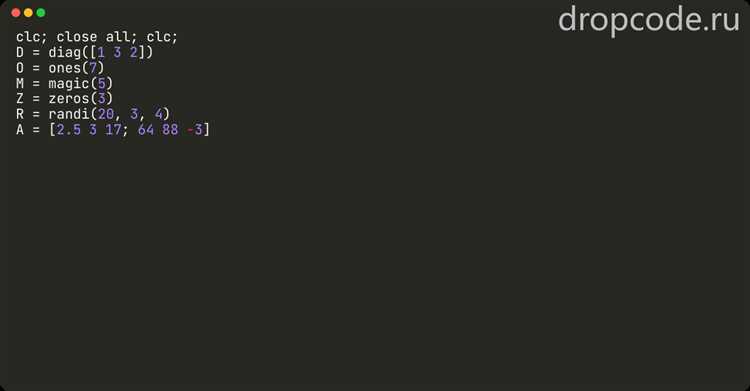
В MATLAB добавление строк или столбцов к матрице выполняется путём индексной операции присваивания. Если имеется матрица A размером 3×3, добавление новой строки осуществляется так: A(4,:) = [10 20 30]. MATLAB автоматически расширяет матрицу, заполняя недостающие элементы нулями, если индекс превышает текущие размеры.
Чтобы добавить столбец, используется следующая форма: A(:,4) = [100; 200; 300]. Важно, чтобы количество элементов в векторе совпадало с числом строк в A, иначе возникнет ошибка несовместимости размеров.
Добавление нескольких строк сразу: A(end+1:end+2,:) = [40 50 60; 70 80 90]. Аналогично для столбцов: A(:,end+1:end+2) = [400; 500; 600; 700; 800], если A имеет 5 строк.
Рекомендуется использовать end+1 вместо явного указания размеров – это упрощает масштабирование кода. При необходимости добавления нулевой строки: A(end+1,:) = 0, если требуется только структура без значений.
Для симметричных операций полезна функция padarray из Image Processing Toolbox, но она не входит в базовый MATLAB. При добавлении строк/столбцов внутри матрицы используйте конкатенацию: A = [A(1:2,:); newRow; A(3:end,:)] – вставка строки между второй и третьей строками.
Следует избегать поэлементного расширения в цикле, так как это приводит к фрагментации памяти. Эффективнее заранее определить итоговый размер матрицы и использовать индексацию для присвоения.
Чтение матриц из внешних файлов в формате.txt и.csv
Для загрузки матриц из файлов .txt и .csv в MATLAB применяются специализированные функции с учётом структуры данных. В файлах .txt матрицы часто записываются с разделителями – пробелами, табуляцией или запятыми, тогда как .csv предполагает запятые как разделители по умолчанию.
Чтение из .txt осуществляется с помощью функции dlmread или readmatrix. Например, mat = dlmread('data.txt', '\t'); загружает матрицу, где столбцы разделены табуляцией. При использовании readmatrix можно не указывать разделитель явно, если файл содержит стандартные разделители:
mat = readmatrix('data.txt');
Если в файле присутствуют заголовки или смешанные типы данных, предпочтительно использовать readtable с последующим преобразованием в массив через table2array.
Чтение из .csv оптимально выполняется функцией readmatrix или csvread. csvread устарела и не поддерживает пропущенные данные, поэтому рекомендуется readmatrix:
mat = readmatrix('data.csv');
Если в файле содержатся заголовки, необходимо пропустить строки с помощью параметра opts:
opts = detectImportOptions('data.csv');
opts.DataLines = 2;
mat = readmatrix('data.csv', opts);
При работе с большими файлами для повышения скорости можно использовать memory mapping или читать данные частями через datastore.
Важно проверять корректность размеров загруженной матрицы и приводить данные к нужному типу с помощью double, single или int* при необходимости. Для текстовых данных, включающих числа с плавающей точкой, правильный выбор кодировки файла и разделителя гарантирует точную загрузку.
Вопрос-ответ:
Какие способы создания матриц доступны в MATLAB?
В MATLAB можно создавать матрицы несколькими способами: вручную, задавая элементы через квадратные скобки с разделением пробелами или точками с запятой для строк, использовать встроенные функции, такие как zeros для нулевой матрицы, ones для матрицы из единиц, eye для единичной матрицы, а также создавать матрицы с помощью функций rand и randn для случайных чисел. Кроме того, можно задавать матрицы с помощью циклов или считывать из файлов.
Как задать матрицу 3×3 с элементами от 1 до 9 без перечисления всех чисел?
Для создания матрицы 3×3 с элементами от 1 до 9 можно использовать функцию reshape: сначала создать вектор с числами от 1 до 9 с помощью 1:9, а затем преобразовать его в матрицу нужного размера с помощью reshape(1:9, 3, 3). Важно помнить, что MATLAB заполняет матрицу по столбцам, поэтому итоговая матрица будет выглядеть так:
1 4 7
2 5 8
3 6 9
Можно ли создавать матрицы с разным типом данных в MATLAB?
В MATLAB матрица — это массив чисел одного типа, поэтому элементы внутри одной матрицы должны иметь одинаковый тип данных (например, все double или все int). Для хранения данных разных типов лучше использовать таблицы или структуры. Если попытаться создать матрицу с элементами разных типов, MATLAB автоматически приведёт все значения к одному общему типу, чаще всего к типу с большей точностью.
Как создать матрицу с помощью циклов в MATLAB?
Создание матрицы с помощью циклов заключается в инициализации пустой матрицы нужного размера, например, через zeros, а затем заполнении её значениями в циклах for. Например:
mat = zeros(3,3);
for i = 1:3
for j = 1:3
mat(i,j) = i + j;
end
end
Такой код создаст матрицу, где каждый элемент равен сумме индексов строки и столбца. Такой подход полезен, когда значения элементов вычисляются по определённой формуле.
Как задать матрицу с элементами, отличающимися на постоянную величину, используя MATLAB?
Для создания матрицы с элементами, изменяющимися на постоянную величину, можно использовать функции linspace или colon. Например, чтобы создать строку из 5 элементов, начинающуюся с 2 и с шагом 3, пишут: 2:3:14 (результат — [2 5 8 11 14]). Для матрицы можно комбинировать такие векторы с функцией repmat или использовать meshgrid для двумерных последовательностей. Эти методы позволяют быстро задавать матрицы с регулярными шаблонами значений.