Как найти экстремум функции mathcad

В Mathcad реализованы численные методы нахождения экстремумов, позволяющие вычислить минимум или максимум функции одной или нескольких переменных без аналитического дифференцирования. Ключевым инструментом служит встроенная функция minimize или maximize, которые работают с заданной функцией и начальными приближениями для переменных.

Для корректной работы метода требуется заранее задать начальное приближение – вектор или скаляр, от которого начинается поиск. Выбор точки старта существенно влияет на результат, особенно при наличии нескольких локальных экстремумов. Поэтому рекомендуется визуализировать график функции или выполнить предварительный анализ, чтобы избежать попадания в ложный экстремум.

Функции minimize и maximize принимают на вход определённую пользователем функцию и вектор начальных значений. Например, при поиске минимума функции двух переменных f(x, y), необходимо определить её как f := (x, y) → выражение, и затем вызвать minimize(f, [x₀, y₀]). Возвращаемый результат – вектор значений переменных, при которых достигается минимум.

Следует учитывать, что Mathcad использует итерационные численные методы, основанные на градиентных алгоритмах. Это означает, что функции должны быть непрерывными и желательно гладкими в области исследования. Разрывы или участки с неограниченными производными могут привести к сбоям или некорректным результатам.

Для ограничения области поиска можно воспользоваться логикой внутри самой функции, например, возвратить очень большие значения за пределами допустимого диапазона, тем самым «наказав» нежелательные участки пространства. Это особенно полезно при решении задач с ограничениями, поскольку встроенные функции экстремизации не поддерживают явные ограничения.

Построение графика функции для визуального определения экстремума

Mathcad предоставляет встроенные инструменты для построения графиков, позволяющие точно локализовать экстремальные точки функций. Графическое представление особенно эффективно при анализе сложных функций, где аналитический способ затруднён или невозможен.

1. Определите диапазон переменной, охватывающий предполагаемую область экстремума. Например, для функции f(x) = x·sin(x) выберите интервал от −10 до 10.
2. Создайте массив значений аргумента:
   • Введите: x := −10, −9.9..10
   • Mathcad автоматически интерпретирует шаг равным 0.1
3. Определите функцию: f(x) := x·sin(x)
4. Постройте график:
   • Вставьте 2D-график
   • На ось X – перетащите массив x
   • На ось Y – f(x)
5. Увеличьте масштаб интересующих участков с подозрением на экстремум, например, область около x = 0, x ≈ ±7.

Для повышения точности:

• Уменьшите шаг массива x до 0.01 или 0.001
• Используйте перетаскивание курсора на графике для выделения области с резкими изменениями значений

Если график показывает наличие локального минимума или максимума, зафиксируйте координаты этих точек и переходите к численному поиску экстремума, используя встроенные функции minimize и maximize.

Использование функции maximize для поиска максимума

Функция maximize в Mathcad предназначена для нахождения максимального значения функции при заданных ограничениях и начальных приближениях. Она возвращает значения переменных, при которых функция достигает локального максимума.

Синтаксис: maximize(f(x), x), где f(x) – целевая функция, x – переменная или вектор переменных. Используется только внутри блока Given-Find, совместно с условиями на переменные.

Перед применением maximize необходимо задать начальные значения переменных, иначе Mathcad не сможет построить область поиска. Пример:

x := 1
maximize(f(x), x)

Если функция зависит от нескольких переменных, необходимо использовать вектор переменных и задать начальные значения для каждой. Пример:

x := 1
y := 2
maximize(f(x, y), [x, y])

Для корректной работы необходимо ограничить область поиска с помощью неравенств. Без ограничений результат может быть недостоверным. Ограничения задаются перед вызовом maximize в блоке Given:

Given
x > 0
x < 10
maximize(f(x), x)

Функция не гарантирует нахождение глобального максимума – только локального вблизи начальной точки. Рекомендуется тестировать разные стартовые значения для повышения достоверности результата.

Применение функции minimize для нахождения минимума

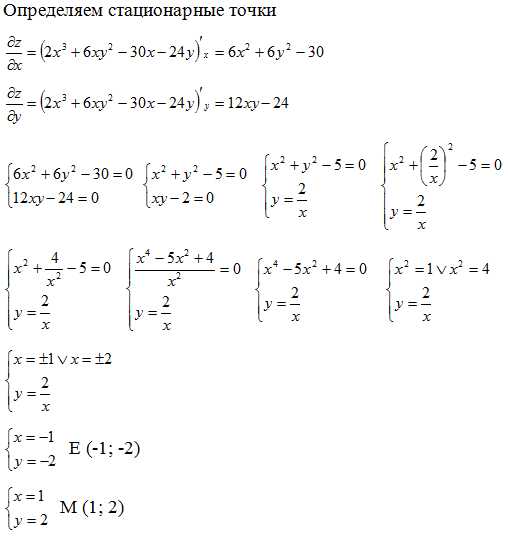
Функция minimize в Mathcad используется для численного поиска минимума многофакторной функции. Она возвращает значения переменных, при которых достигается минимальное значение целевой функции. Функция требует начального приближения и определения переменных оптимизации с помощью оператора :=.

Синтаксис: minimize(f(x), x), где f(x) – скалярная функция, а x – вектор начальных значений переменных.

Перед использованием minimize необходимо определить все переменные и параметры функции. Рекомендуется использовать хорошо подобранные начальные приближения, особенно при наличии нескольких локальных минимумов. Для заданий с ограничениями функция minimize не подходит – в таких случаях используется minerr.

Пример задачи:

f(x, y) := (x - 3)^2 + (y + 1)^2
xy := [0, 0
]
result := minimize(f(xy[0,0], xy[1,0]), xy)

В результате result содержит координаты точки минимума: [3, -1].

Если необходимо минимизировать функцию от большего числа переменных, используйте вектор начальных значений соответствующей размерности. Mathcad выполняет оптимизацию методом квазиньютоновского типа, поэтому функции должны быть гладкими и дифференцируемыми.

Рекомендуется проверять полученное решение подстановкой в исходную функцию для контроля корректности. Также полезно визуализировать поведение функции с помощью графиков до и после оптимизации.

Указание начального приближения и его влияние на результат

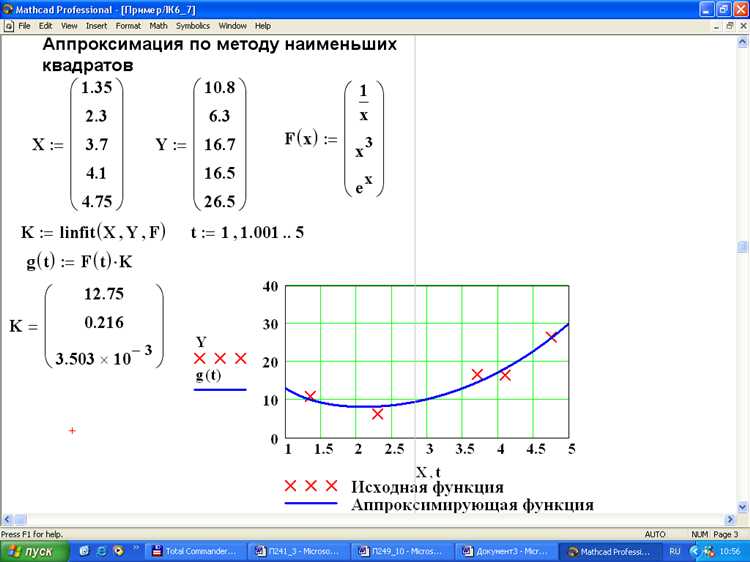
В Mathcad поиск экстремума функции осуществляется численными методами, которые требуют задания начального приближения. Этот параметр критически важен, так как определяет, к какому локальному экстремуму сойдётся алгоритм. При отсутствии подходящего приближения метод может не сойтись вовсе или вернёт значение, не соответствующее ожидаемому экстремуму.

Например, при использовании функции minimize(f(x), x), Mathcad применяет градиентный спуск. Если начальная точка находится вблизи седловой точки или плато, производная становится близкой к нулю, и алгоритм прекращает работу без нахождения минимума. Аналогичная ситуация наблюдается с maximize при поиске максимума.

Рекомендуется перед применением оптимизационных функций анализировать поведение функции графически: построить f(x) в диапазоне интереса и вручную определить участки, где вероятно расположение экстремума. Начальное приближение следует выбирать максимально близко к предполагаемому экстремуму, чтобы уменьшить риск попадания в нежелательный локальный минимум или максимум.

Для функций с несколькими экстремумами необходимо запускать оптимизацию с разных стартовых точек. Это позволяет определить все возможные локальные экстремумы и выбрать из них глобальный. Например, при поиске минимума функции f(x) = x⁴ — 3x³ + 2, начальные приближения x := 0 и x := 2 приводят к разным результатам: ≈1.08 и ≈2.62 соответственно.

В случае многомерных функций (f(x, y, …)) выбор начального приближения становится ещё более критичным. Рекомендуется использовать визуализацию уровня функции или проводить срезы по переменным для оценки рельефа и подбора начальных координат.

Ошибки округления и выбор плохой стартовой точки особенно чувствительны при плоских экстремумах. В таких ситуациях необходимо увеличивать точность расчётов (TOL) и при необходимости масштабировать переменные.

Решение задач с ограничениями при поиске экстремума

В Mathcad задачи поиска экстремума с ограничениями решаются с использованием встроенной функции maximize или minimize совместно с системой уравнений, определяющих допустимую область. При этом ограничения задаются в виде логических выражений внутри блока Given.

Для примера, пусть требуется найти максимальное значение функции f(x, y) = x·y при ограничениях: x + y ≤ 10, x ≥ 0, y ≥ 0. В Mathcad необходимо ввести блок Given и задать условия:

Given

y ≥ 0

Затем используется вызов maximize(f(x, y), (x, y)), при этом переменные x и y должны быть объявлены как неизвестные ранее в том же блоке.

Если ограничения выражаются в виде уравнений (например, x² + y² = 25), используется метод Лагранжа. В этом случае создается система из уравнений: градиент функции равен градиенту ограничения, умноженному на множитель Лагранжа. Решение проводится с помощью функции solve или блока Find с соответствующими уравнениями.

Для повышения стабильности решений с ограничениями рекомендуется:

• Задавать начальные приближения как можно ближе к предполагаемому экстремуму.
• Проверять выполнение ограничений вручную после получения результата.
• Использовать явно заданные границы через условные выражения, а не только через уравнения.

Mathcad не поддерживает неявные ограничения напрямую, поэтому для сложных условий рекомендуется их явная трансформация или использование вспомогательных переменных.

Анализ ошибок и диагностика некорректных решений

Наиболее частая ошибка при поиске экстремума в Mathcad – неправильный выбор начального приближения. Функция minimize или maximize чувствительна к исходной точке: при многомодальных функциях она может привести к локальному экстремуму вместо глобального. Рекомендуется анализировать график функции перед использованием численных методов.

Вторая типичная проблема – отсутствие сходимости. Если Mathcad возвращает ошибку «No solution was found», это может указывать на разрыв функции, вертикальную асимптоту в области поиска или слишком резкий градиент. В таких случаях необходимо изменить начальные условия, сократить область поиска или использовать сглаженную аппроксимацию функции.

Неправильная передача аргументов – ещё один источник некорректных решений. Функции оптимизации требуют строго определённого синтаксиса: аргументы должны быть заданы в виде вектора, а сама функция – принимать вектор как входной параметр. Например, f(x):=x[0]^2+x[1]^2 корректно, а f(x,y):=x^2+y^2 – нет.

Ошибки единиц измерения также критичны. Mathcad учитывает размерности, и несовпадение единиц в аргументах и функции приводит к отказу алгоритма. Всегда приводите переменные к безразмерному виду или строго следите за единицами.

Для диагностики рекомендуется: построить график функции в предполагаемой области экстремума, проанализировать поведение градиента, использовать оператор trace для отслеживания промежуточных значений, а также сравнивать результаты с аналитическими методами там, где это возможно.

Вопрос-ответ:

Как найти максимум функции в Mathcad, если у неё несколько переменных?

Для поиска максимума функции от нескольких переменных в Mathcad можно использовать встроенную функцию **maximize(f(x, y, …), x, y, …)**. Однако она требует указания начальных приближений для всех переменных. Важно, чтобы начальные значения были выбраны достаточно близко к предполагаемому экстремуму, иначе результат может оказаться локальным, а не глобальным максимумом. Mathcad использует численные методы, поэтому результат зависит от начальных условий и формы функции.

Можно ли использовать Mathcad для нахождения экстремума дискретной функции?

Mathcad в основном рассчитан на работу с непрерывными функциями. Для дискретных данных лучше использовать перебор значений с помощью массива и функции поиска максимального или минимального значения. Например, можно создать вектор значений функции и применить **max(vector)** или **min(vector)**. Если необходима не только величина, но и соответствующий аргумент, то придётся использовать оператор **position** или сравнение значений вручную через цикл или логическое условие.

Почему Mathcad иногда находит минимум вместо максимума (или наоборот)?

Mathcad использует численные алгоритмы для поиска экстремумов, и результат может зависеть от выбора начальных значений. Если используется функция **maximize**, но начальное приближение ближе к минимуму, Mathcad может «сойтись» именно к нему, особенно если максимум находится далеко или его область притяжения меньше. Чтобы этого избежать, стоит исследовать график функции и выбирать начальные условия осознанно. Также полезно попробовать несколько стартовых точек и сравнить результаты.

Чем отличаются функции maximize и minerr в Mathcad при поиске экстремума?

Функция **maximize** используется напрямую для поиска максимального значения функции при заданных переменных. **minerr**, в свою очередь, минимизирует выражение ошибки — чаще всего это отклонение от заданного значения или условия. **minerr** может применяться, когда нужно найти параметры, при которых функция достигает определённого поведения (например, равенство нулю). В случае поиска минимума или максимума напрямую **maximize** и **minimize** проще и нагляднее, но **minerr** даёт больше гибкости при настройке условий.

Как понять, экстремум ли найденной точки — максимум, минимум или седловая точка?

Mathcad сам по себе не проводит анализ второго порядка, чтобы различать типы экстремума. Если функция имеет несколько переменных, можно использовать численное приближение для оценки частных производных второго порядка (второй производной или гессиана). Это позволит определить характер точки. В более простых случаях достаточно построить график функции в окрестности найденной точки — если поведение функции указывает на рост или убывание от неё, можно судить о типе экстремума.