Как в mathcad задать производную

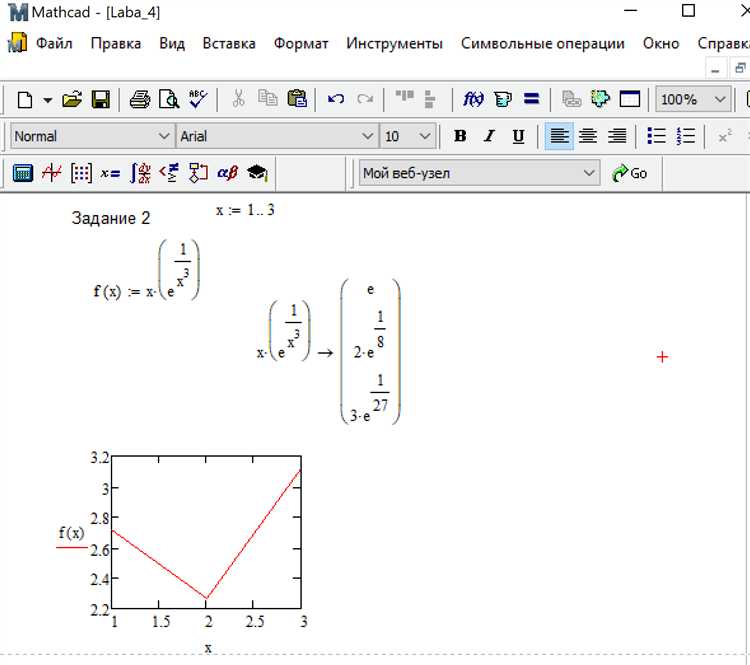
В Mathcad производная функции задаётся через встроенные операторы, которые обеспечивают точные численные и символьные вычисления. Для вычисления производной первого порядка достаточно использовать оператор дифференцирования с символом апострофа (‘) после имени функции. Например, f'(x) возвращает значение производной функции f в точке x.

Для определения производной в конкретной точке удобно применять оператор deriv, который принимает три аргумента: функцию, переменную и значение точки. Такой подход гарантирует точное численное значение, что особенно важно при сложных аналитических выражениях.

Mathcad также поддерживает вычисление производных высших порядков, используя повторное применение апострофов, например, f»(x) для второй производной. При необходимости можно задать производную вручную через пределы или определить её с помощью встроенных инструментов символической обработки, что повышает гибкость при работе с нестандартными функциями.

Определение символической производной в Mathcad

Для вычисления символической производной в Mathcad необходимо использовать встроенные функции работы с символьной алгеброй. В основе лежит оператор d(), который позволяет задать производную по переменной для заданного выражения.

• Синтаксис: d(выражение, переменная), где выражение – функция или выражение, а переменная – символ, по которому берется производная.
• Перед использованием оператора убедитесь, что переменная объявлена как символьная, а не числовая.
• Для этого в Mathcad достаточно ввести переменную без присваивания числового значения, или использовать функцию symbol() для явного задания символа.

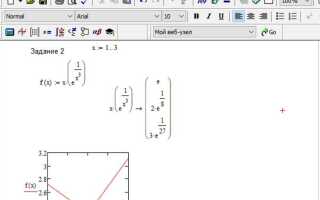
Пример вычисления производной функции f(x) = x^3 + 2x по переменной x:

1. Объявить переменную: x := symbol().
2. Задать функцию: f := x^3 + 2*x.
3. Вычислить производную: df_dx := d(f, x).

В результате Mathcad выведет выражение 3*x^2 + 2, что является аналитической формой производной.

Для производных высших порядков указывается дополнительный аргумент – порядок производной. Например, вторая производная функции:

• d(f, x, 2) – вторая производная по x.

Mathcad также позволяет использовать оператор производной непосредственно к выражению без необходимости создавать отдельную функцию, что ускоряет расчет и упрощает структуру документа.

Задание численной производной с помощью оператора D

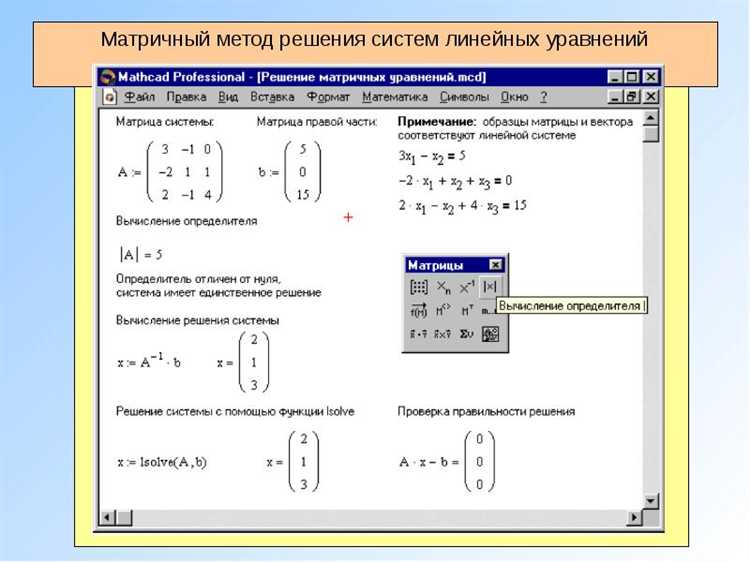
В Mathcad оператор D применяется для вычисления численных производных функций, заданных в виде дискретных данных или выражений. Формат записи производной: D(f(x), x), где f(x) – функция или массив значений, x – переменная.

Для корректной работы оператор D требуется равномерная сетка значений переменной. Если точки заданы неравномерно, вычисления производной могут дать искажения. В таких случаях рекомендуется использовать интерполяцию функции перед применением D.

Оператор D вычисляет первую производную, используя разностные методы, учитывая соседние точки. Для второго порядка производной применяется запись D(D(f(x), x), x). Mathcad автоматически определяет шаг сетки из входных данных.

Для функций, определённых аналитически, предпочтительно задавать выражение напрямую, чтобы оператор D применялся к формуле, а не к таблице значений. Это повышает точность и скорость вычислений.

Чтобы получить производную по конкретной точке, необходимо указать точку в аргументах: D(f(x), x, x0), где x0 – значение переменной, в котором вычисляется производная. Если точка не указана, Mathcad вернёт массив значений производной по всей сетке.

При работе с массивами оператор D возвращает массив производных, соответствующий размерности входных данных, за исключением граничных элементов, где точность может снижаться.

Использование функции diff для вычисления производных

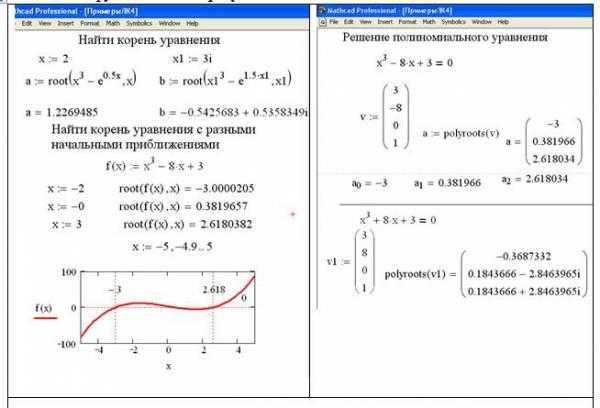
В Mathcad функция diff применяется для численного вычисления производной функции, заданной дискретно или аналитически. Ее синтаксис: diff(выражение, переменная, порядок, шаг), где обязательны первые два параметра.

Параметр выражение – это функция или числовой вектор значений функции. переменная – независимая переменная, по которой берется производная. порядок указывает, какую производную считать (по умолчанию 1). шаг задает величину приращения переменной (необязательный параметр, по умолчанию выбирается автоматически).

Для аналитических функций рекомендуется использовать символическую форму записи: например, diff(sin(x), x) вернет выражение косинуса. При численных данных функция вычисляет производную методом конечных разностей с учетом заданного шага.

Важно, что точность численного дифференцирования напрямую зависит от параметра шаг. Слишком большой шаг снижает точность, слишком маленький увеличивает ошибки округления. Рекомендуется подбирать оптимальный шаг экспериментально, начиная с порядка 0.01 или 0.001 от диапазона переменной.

Для высоких порядков производных указывайте параметр порядок явно, например, diff(f(x), x, 2) вычисляет вторую производную. При этом необходимо следить за достаточным количеством точек данных для корректного результата.

Использование diff эффективно для быстрой оценки производных при анализе графиков и численных экспериментах, когда аналитическое дифференцирование затруднено или невозможно.

Настройка порядка производной в выражениях Mathcad

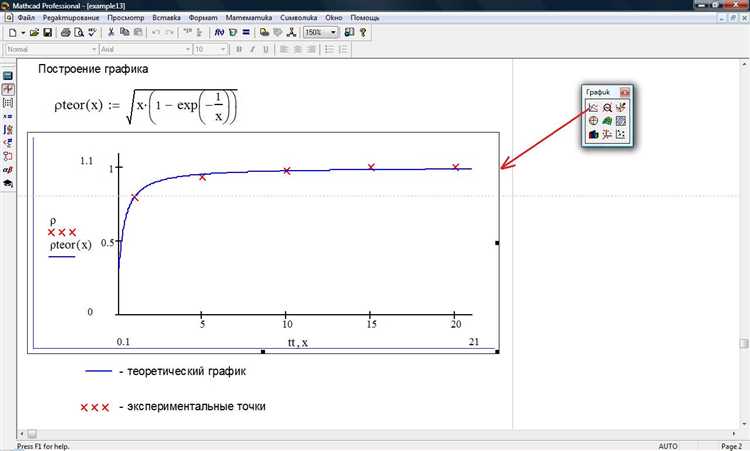
Для задания порядка производной в Mathcad используется символ дифференцирования с указанием индекса степени. Стандартный синтаксис – оператор дифференцирования, например, d/dx, с последующим числом, обозначающим порядок, в виде верхнего индекса или функции diff.

При вводе производной высокого порядка применяют функцию diff(f(x), x, n), где n – целое число, определяющее порядок. Это позволяет вычислить производную произвольного порядка без необходимости многократного применения оператора d/dx вручную.

Для удобства и визуальной наглядности можно использовать встроенные элементы Mathcad: при вводе выражения производной нажатием сочетания клавиш Ctrl+Shift+D открывается диалог для выбора переменной и порядка. В поле порядка указывайте нужное значение, начиная с 1.

В выражениях с несколькими переменными дифференцирование по определённой переменной настраивается через дифференциальный оператор с её указанием, а порядок задаётся дополнительным параметром функции diff, например diff(f(x,y), y, 2) – вторая производная по y.

Важно учитывать, что Mathcad различает полные и частные производные, поэтому для частных производных обязательно указывать переменную, а порядок – через аргумент функции diff.

При построении графиков с производными высокого порядка рекомендуется предварительно сохранить результат вычисления в отдельную переменную для повышения скорости обновления и упрощения дальнейших вычислений.

Применение производных к пользовательским функциям

В Mathcad производные можно задавать не только для встроенных функций, но и для пользовательских, что расширяет возможности анализа. Для этого необходимо определить функцию с помощью оператора := и указать аргументы в круглых скобках.

Для вычисления производной функции f(x) по переменной x используют оператор дифференцирования ‘ (штрих) после имени функции, например, f'(x). При этом Mathcad автоматически применит правила дифференцирования к формуле, заданной пользователем.

Если функция многомерная, например, f(x,y), производную можно взять по конкретной переменной, указав её через запятую: ∂f/∂x или обозначив частную производную как diff(f(x,y),x). Для сокращения записи удобно использовать встроенную функцию diff.

При работе с пользовательскими функциями рекомендуется явно прописывать все переменные и использовать понятные имена, чтобы избежать ошибок в дифференцировании. Кроме того, Mathcad корректно обрабатывает сложные выражения, содержащие тригонометрические, экспоненциальные и логарифмические функции.

Если нужно вычислить производную в конкретной точке, достаточно подставить значение аргумента после дифференцирования, например, f'(2). Mathcad выдает численное значение без дополнительного преобразования.

Для более сложных задач, например, когда функция зависит от параметров, дифференцирование выполняется по выбранной переменной без изменения параметров. Это полезно при построении аналитических выражений для оптимизации и моделирования.

Графическое отображение производной на примере функции

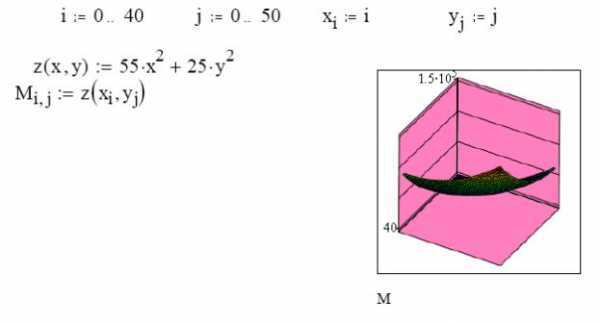
Для визуализации производной функции в Mathcad необходимо сначала определить исходную функцию. Например, зададим функцию f(x) := x^3 - 4x^2 + 6x - 2. Далее вычислим её производную с помощью оператора дифференцирования: fʹ(x) := diff(f(x), x).

После этого создадим график исходной функции, используя стандартный инструмент построения графиков. В окне построения указываем диапазон значений переменной x, например от 0 до 4, чтобы охватить важные особенности функции.

Для наложения графика производной на тот же координатный тракт создайте второй график с функцией fʹ(x) в том же диапазоне. Важно задать разные цвета для графиков, чтобы четко различать исходную функцию и её производную.

Для повышения информативности добавьте на график ключевые точки, например, точки экстремумов исходной функции, которые соответствуют нулевым значениям производной. Найти эти точки можно решением уравнения fʹ(x) = 0 в Mathcad с помощью функции root().

Используйте возможность Mathcad изменять масштаб и сетку графика для детального рассмотрения поведения функции и её производной в области интереса. Таким образом, визуализация позволяет сразу увидеть взаимосвязь между функцией и её наклоном в каждой точке.

Работа с частными производными в Mathcad

В Mathcad частные производные вычисляются с помощью встроенной функции частного дифференцирования, обозначаемой как ∂ или partial. Для задания частной производной необходимо явно указать переменную, по которой происходит дифференцирование.

Синтаксис частной производной в Mathcad выглядит так: ∂(f(x,y), x) – производная функции f по переменной x, при этом y считается постоянной. Аналогично, ∂(f(x,y), y) вычисляет производную по y.

Для функций с более чем двумя переменными можно задавать частные производные по любым переменным, перечисленным в аргументах функции. При необходимости вычисления смешанных производных используется вложенный вызов, например, ∂(∂(f(x,y), x), y) – вторая производная сначала по x, затем по y.

Mathcad позволяет использовать частные производные как символические выражения и сразу подставлять численные значения переменных, что удобно для анализа и визуализации. Для численного вычисления производных достаточно определить функцию и подставить значения переменных в выражение частной производной.

При работе с частными производными важно задавать функции в явном виде и избегать неопределённостей, чтобы Mathcad корректно распознал переменные дифференцирования. Также следует учитывать, что Mathcad чувствителен к синтаксису, поэтому скобки и порядок аргументов должны строго соответствовать требованиям.

Отладка и проверка правильности вычисления производных

Для подтверждения корректности вычисления производной в Mathcad важно использовать системный подход, основанный на конкретных проверках и сравнениях.

1. Аналитическое сравнение с известными производными.

   • Для элементарных функций (например, sin(x), exp(x), x^n) вручную вычислите производную и сравните с результатом Mathcad.

2. Численная проверка производной через конечные разности.

   • Рассчитайте производную в точке x0 с помощью Mathcad.
   • Параллельно вычислите численное приближение производной по формуле (f(x0+h) — f(x0))/h при достаточно малом шаге h (например, h=10^-6).
   • Сравните результаты, учитывая возможную погрешность численного метода.

3. Проверка на нескольких точках.

   • Вычислите производную в нескольких точках из области определения функции.
   • Проанализируйте закономерность изменения производной: отсутствие резких скачков для гладких функций или соответствие особенностям функции.

4. Использование графиков для визуальной проверки.

   • Постройте график исходной функции и ее производной на одном интервале.
   • Проверьте, что касательная к функции в точке x0 совпадает с наклоном графика производной в этой точке.

5. Проверка дифференцирования сложных выражений.

   • Разложите сложную функцию на составные части и проверьте производные каждой из них отдельно.
   • Сравните производную сложной функции с результатом по правилу дифференцирования произведения, частного или композиции.

6. Валидация через альтернативные методы Mathcad.

   • Используйте как символьное, так и численное дифференцирование и сравните результаты.
   • Если присутствует встроенный модуль CAS, проверьте вычисления через него.

Соблюдение этих процедур позволяет обнаружить ошибки в формулировках функций, в выборе аргументов, а также выявить возможные баги в настройках Mathcad.

Вопрос-ответ:

Как в Mathcad задать производную функции с помощью стандартных операторов?

В Mathcad можно определить производную функции, используя встроенный оператор дифференцирования. Для этого достаточно написать функцию, а затем применить к ней символ апострофа (‘) или функцию deriv. Например, если задана функция f(x), производная будет записываться как f'(x) или deriv(f(x), x). Такой подход позволяет быстро получить аналитическое выражение производной без необходимости вручную рассчитывать пределы.

Можно ли в Mathcad вычислить производную в конкретной точке?

Да, Mathcad позволяет вычислять значение производной функции в заданной точке. После задания производной символом апострофа или функцией deriv достаточно подставить нужное значение аргумента. Например, если f'(x) — производная, то f'(2) вернет численное значение производной в точке x=2. Это удобно для анализа поведения функции в отдельных точках.

Как задать производную высших порядков в Mathcad?

Для вычисления производных второго и более высоких порядков в Mathcad используется многократное применение оператора апострофа или параметр функции deriv. Например, вторая производная функции f(x) записывается как f»(x) или deriv(f(x), x, 2). Число после x указывает порядок дифференцирования. Это позволяет получать точные выражения для сложных функций и анализировать их поведение с учетом кривизны и других характеристик.

Можно ли задать производную функции, заданной таблично, а не аналитически?

Если функция задана набором дискретных значений в виде таблицы, то для вычисления производной в Mathcad применяют численные методы. Например, можно использовать оператор разностных частных или встроенные функции для численного дифференцирования, которые приближенно рассчитывают производную на основе значений функции в соседних точках. Такой способ не дает аналитической формулы, но позволяет получить приближенные результаты для дальнейшего анализа.

Как правильно использовать оператор deriv для сложных функций с несколькими переменными в Mathcad?

В Mathcad оператор deriv позволяет вычислять частные производные функций нескольких переменных. При задании функции f(x, y) для получения производной по x нужно использовать deriv(f(x, y), x), а для производной по y — deriv(f(x, y), y). Это особенно полезно при работе с многомерными задачами, где важно понимать изменение функции по каждому параметру отдельно. Можно также комбинировать дифференцирование по разным переменным для получения смешанных производных.