Как выделить мнимую и действительную часть в mathcad

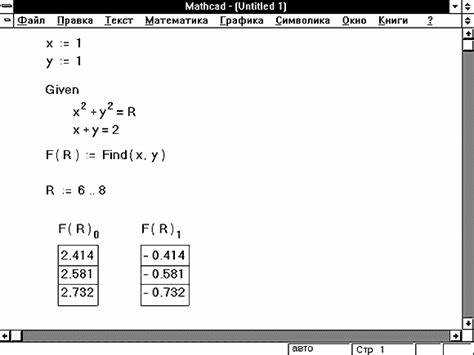
Mathcad предоставляет встроенные функции для точного разделения комплексных чисел на действительную и мнимую части. Для выделения действительной части используется функция real(), а для мнимой – imag(). Эти функции возвращают числовые значения, что позволяет применять их в дальнейших вычислениях и построении графиков.

При работе с комплексными выражениями важно учитывать формат ввода данных: Mathcad воспринимает комплексные числа в форме a + b*i, где i – мнимая единица. Ошибки при вводе, например, пропуск знака умножения перед i, могут привести к некорректным результатам при выделении частей.

Рекомендуется использовать функции real() и imag() совместно с проверкой типа данных с помощью iscomplex(). Это позволяет избежать ошибок при обработке чисто действительных чисел и повысить надежность расчетов в инженерных задачах.

Работа с комплексными числами в Mathcad: базовые операции

В Mathcad комплексные числа задаются через оператор "i" (мнимая единица). Например, комплексное число 3 + 4i вводится как 3 + 4*i. Для создания комплексных чисел можно использовать и функцию complex(x, y), где x – действительная часть, y – мнимая.

Сложение и вычитание комплексных чисел выполняются стандартно через знаки + и -. Умножение и деление обозначаются * и /. При делении Mathcad автоматически упрощает выражение и сохраняет результат в комплексном виде.

Для получения действительной части комплексного числа используют функцию real(z), а для мнимой – imag(z). Модуль комплексного числа вычисляется функцией abs(z), а аргумент – arg(z), где z – комплексное число.

Комплексное сопряжение реализуется через функцию conj(z). При работе с векторами и матрицами комплексных чисел Mathcad позволяет выполнять операции поэлементно, сохраняя размерность и тип данных.

Для преобразования из полярной формы в алгебраическую используют функцию rect(r, θ), где r – модуль, θ – аргумент (в радианах). Обратное преобразование в полярную форму – polar(z), возвращает вектор из двух элементов: модуль и аргумент.

Использование функции real() для получения действительной части

В Mathcad функция real() извлекает действительную часть комплексного числа, представленную в стандартном формате. Она принимает на вход переменную или выражение с комплексным значением и возвращает число без мнимой составляющей.

Для корректного применения real() важно учитывать формат входных данных. Например, при работе с комплексными переменными, созданными через оператор i или j, функция возвращает числовое значение реальной части без округления и преобразований. Результат сохраняет числовой тип данных.

Пример использования: real(3 + 4*i) = 3. При работе с вектором или матрицей комплексных чисел real() применяется поэлементно, возвращая массив из действительных частей.

Если аргумент функции является вещественным числом, результатом будет то же число без изменений, что позволяет использовать real() универсально без дополнительной проверки типа.

В случаях, когда комплексное значение задано в тригонометрической или экспоненциальной форме, для получения действительной части сначала рекомендуется привести выражение к алгебраической форме, используя функции rect() или аналогичные, а затем применить real().

При вычислениях с переменными, содержащими погрешности или числовые приближения, функция real() не изменяет точность, но для чистоты результата можно дополнительно использовать округление.

Применение функции imag() для извлечения мнимой части

В Mathcad функция imag() служит для получения мнимой составляющей комплексного числа. Она принимает на вход числовое выражение с комплексным значением и возвращает только мнимую часть в виде вещественного числа.

Для корректной работы imag() необходимо убедиться, что аргумент действительно содержит мнимую компоненту. Если входное значение – чисто действительное число, результатом будет ноль. В случае комплексных переменных или выражений с комплексными коэффициентами функция извлечёт коэффициент при мнимой единице.

Функция особенно полезна при анализе комплексных сигналов и решении задач с комплексными корнями. В расчетах, где требуется разделить комплексные результаты на действительную и мнимую части, imag() позволяет изолировать мнимую часть без дополнительных преобразований.

Рекомендуется использовать imag() совместно с функцией real(), если необходимо получить полный анализ комплексного значения. При работе с векторными или матричными данными imag() автоматически применяется поэлементно, что упрощает обработку больших массивов комплексных чисел.

В практических вычислениях следует учитывать, что численные погрешности могут приводить к незначительным отклонениям мнимой части от нуля, даже если теоретически она отсутствует. Для фильтрации таких значений рекомендуется вводить пороговые значения, например, считать мнимую часть нулём при |imag(x)| < 10^-12.

Обработка комплексных выражений в матричных и векторных данных

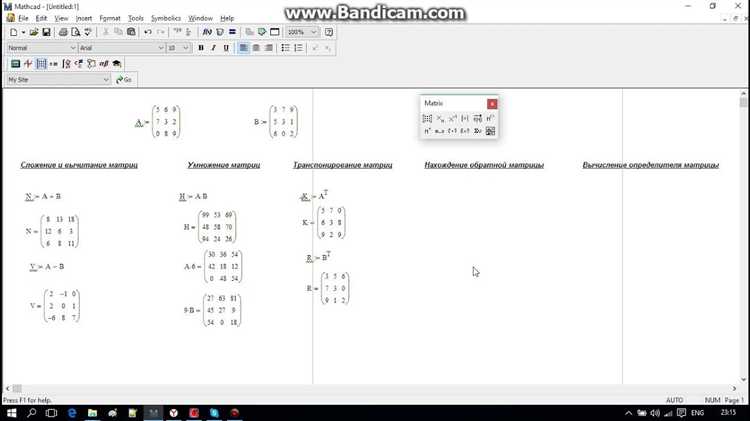
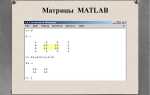
В Mathcad комплексные значения могут быть представлены в матрицах и векторах, что позволяет выполнять параллельные вычисления над множеством данных. Для выделения действительной и мнимой части в таких структурах используются функции real() и imag(), которые работают поэлементно.

При работе с матрицами важно учитывать размерность: применение real() или imag() к матрице возвращает матрицу тех же размеров, где каждый элемент соответствует соответствующей части исходного комплексного числа. Это упрощает дальнейшую обработку, например, построение графиков или расчет статистических характеристик по отдельным компонентам.

Для векторов последовательность действий аналогична. Обработка комплексного вектора с помощью real() и imag() позволяет получить два отдельных вектора, которые можно использовать для анализа амплитудно-фазовых характеристик или для последующих арифметических операций.

При необходимости комбинировать данные рекомендуется избегать смешивания комплексных и вещественных чисел в одном массиве без явного преобразования, чтобы не возникало ошибок при вычислениях. Рекомендуется применять функции complex() для создания комплексных чисел из отдельно заданных действительной и мнимой частей.

Для оптимизации производительности при работе с большими матрицами стоит использовать встроенные функции Mathcad, избегая циклов и ручной обработки элементов. Встроенные операции векторизации значительно ускоряют вычисления и упрощают код.

Автоматическое разделение комплексных чисел при вычислениях

Mathcad автоматически обрабатывает комплексные числа, разделяя их на действительную и мнимую части без дополнительного вмешательства пользователя. При вводе комплексного выражения система воспринимает его как объект с двумя компонентами – Re и Im, что позволяет использовать встроенные функции для их выделения.

Для выделения действительной части достаточно применить функцию Re(), а для мнимой – Im(). Mathcad вычисляет и отображает соответствующие компоненты по мере выполнения расчетов, что обеспечивает точность и прозрачность промежуточных результатов. Это особенно важно при работе с выражениями, содержащими переменные и сложные арифметические операции.

В случае операций с комплексными функциями Mathcad сохраняет корректное распределение действительной и мнимой частей, исключая ошибки, связанные с ручным разделением. Автоматическое выделение облегчает анализ сигналов, электрических цепей и систем с комплексными параметрами, ускоряя построение моделей и их проверку.

Отображение мнимой и действительной частей на графиках Mathcad

Для построения графиков действительной и мнимой частей комплексной функции в Mathcad необходимо сначала получить эти составляющие с помощью встроенных функций real() и imag(). Например, если переменная z содержит комплексное значение, real(z) вернёт действительную часть, а imag(z) – мнимую.

При создании графиков используйте отдельные оси Y для действительной и мнимой частей, чтобы избежать наложения данных. Для этого создайте два отдельных графика или используйте функцию plot с двумя наборами данных, где первый отображает real(z), второй – imag(z).

Для улучшения восприятия рекомендуется добавлять легенды, указывая, какая кривая соответствует действительной части, а какая – мнимой. Подписи осей должны содержать обозначения, например, «Re» и «Im», чтобы исключить неоднозначность.

В случаях, когда анализ проводится по переменной времени или частоты, на оси X указывайте соответствующую физическую величину с правильными единицами измерения. Это позволит получить интерпретируемые графики и упростит анализ.

Если функция меняется в широком диапазоне значений, используйте масштабирование осей или логарифмические оси для отображения всех особенностей. Mathcad поддерживает настройку масштабов в настройках графика.

Для сложных вычислений с комплексными функциями используйте массивы значений, предварительно вычисляя действительную и мнимую части, и передавайте их в графическую функцию. Это ускорит построение и позволит избежать ошибок.

Использование операторов и функций для комбинирования частей числа

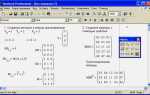
В Mathcad для получения комплексного числа из его действительной и мнимой частей применяются специальные операторы и функции, обеспечивающие точный контроль над формированием результата.

• Оператор комплексного сложения: используется для прямого сложения действительной и мнимой частей, например, Re + i·Im, где Re и Im – действительная и мнимая части соответственно.
• Функция complex()complex(Re, Im). Это обеспечивает явное и читаемое создание комплексного значения.
• Использование оператора i: в Mathcad символ i обозначает мнимую единицу. Умножение мнимой части на i корректно формирует комплексную часть, что позволяет использовать выражения вида Re + i*Im без дополнительных функций.