Как задать функцию в wolfram mathematica

Wolfram Mathematica – это мощная система для вычислений, которая позволяет создавать функции для решения самых разных задач. В этой статье мы рассмотрим, как правильно задать функцию в Mathematica, чтобы она работала эффективно и без ошибок. Важно понимать структуру и синтаксис, так как это позволяет избежать распространенных проблем, таких как неправильные результаты или сбои в коде.

Основным инструментом для определения функции в Mathematica является конструкция Function. Однако важно не только правильно ее использовать, но и понимать, как настраивать параметры функции для получения нужного результата. Если ваша цель – создание функции с несколькими переменными, Mathematica предлагает гибкие механизмы для их обработки и передачи значений.

В первой части руководства мы разберем, как задать простую функцию с одной переменной. Для этого достаточно использовать обычный синтаксис f[x_] := expression, где x_ – это паттерн для входного параметра, а expression – то, что возвращает функция при вызове. В следующем шаге мы покажем, как расширить эту технику на более сложные случаи, например, функции с несколькими параметрами и условными операторами.

Как задать функцию в Wolfram Mathematica: пошаговое руководство

Для того чтобы создать функцию в Wolfram Mathematica, необходимо следовать простому алгоритму. Рассмотрим основные шаги, начиная с самого простого примера.

Шаг 1. Создание базовой функции

Для определения функции в Mathematica используется синтаксис f[x_] := выражение, где f – имя функции, x_ – аргумент функции, а выражение – то, что функция должна вернуть. Например, для создания функции квадрата числа напишем:

f[x_] := x^2

Теперь при вызове f[3] будет возвращено значение 9.

Шаг 2. Определение функции с несколькими аргументами

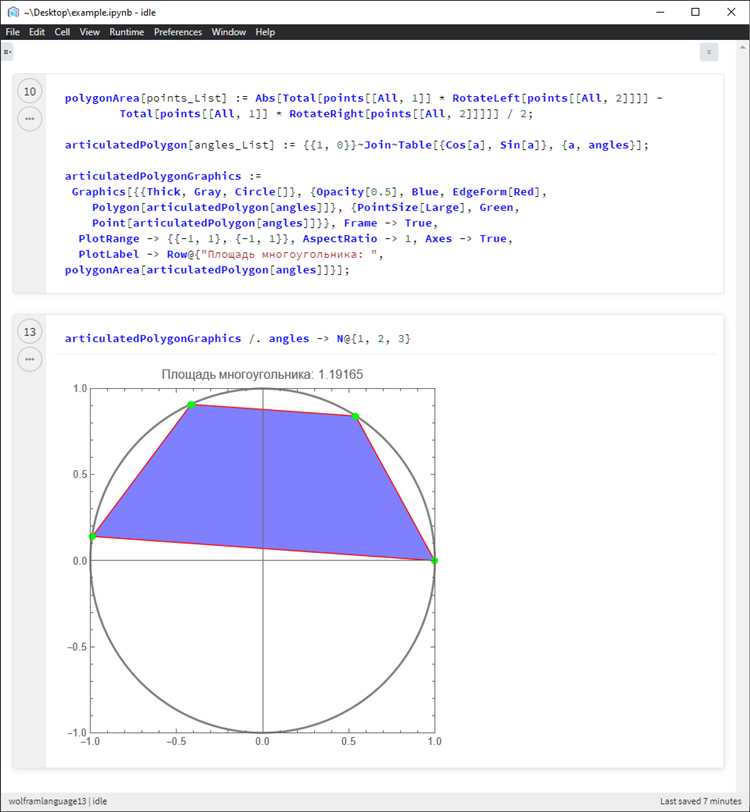
Для функции с несколькими аргументами синтаксис такой же. Например, для функции, которая складывает два числа, нужно использовать следующий код:

g[x_, y_] := x + y

Вызов g[2, 3] вернёт 5.

Шаг 3. Условные выражения в функциях

Для создания более сложных функций, использующих условия, можно использовать конструкцию If. Например, функция, которая возвращает квадрат числа, если оно положительное, и ноль – если отрицательное:

h[x_] := If[x > 0, x^2, 0]

Для вызова h[3] результат будет 9, а для h[-3] – 0.

Шаг 4. Использование встроенных функций и операций

В Mathematica есть множество встроенных функций, которые можно использовать внутри своей. Например, можно вычислить производную функции:

derivative[f[x_]] := D[f[x], x]

Теперь, например, derivative[x^2] вернёт 2 x.

Шаг 5. Функции с несколькими возвращаемыми значениями

Иногда необходимо, чтобы функция возвращала несколько значений. Это можно сделать с помощью Return или просто перечислив значения через запятую. Пример функции, которая возвращает как сумму, так и произведение двух чисел:

sumAndProduct[x_, y_] := {x + y, x * y}

При вызове sumAndProduct[3, 4] результатом будет список {7, 12}.

Шаг 6. Локальные переменные и области видимости

Для ограничения области видимости переменных используется конструкция Module. Например:

myFunction[x_] := Module[{a, b}, a = x^2; b = a + 1; b]

Здесь переменные a и b ограничены областью видимости функции и не будут доступны извне.

Шаг 7. Тестирование и отладка функций

После того как функция определена, важно проверить её на разных входных значениях. Используйте различные примеры, чтобы убедиться в корректности работы. В Mathematica есть инструмент для отладки функций – Trace, который позволяет отслеживать, как выполняется функция и какие промежуточные значения вычисляются.

Теперь вы знаете, как создавать функции в Wolfram Mathematica и какие синтаксические конструкции и техники использовать для расширения функциональности. Эти базовые шаги позволят вам начать работать с математическими выражениями и решать более сложные задачи.

Создание функции с использованием оператора :=

Оператор := в Wolfram Mathematica используется для определения функций с задержанной оценкой. Это означает, что функция не будет вычисляться при ее определении, а только когда она будет вызвана с конкретными аргументами. Такая особенность позволяет динамически изменять поведение функции, например, используя значения переменных или вычисления, которые актуальны на момент выполнения.

Чтобы создать функцию, используя :=, нужно указать ее имя, параметры и тело. Пример базового определения функции:

f[x_] := x^2

В этом примере f – это функция, которая принимает один параметр x и возвращает квадрат этого значения. Оператор := говорит Mathematica, что это определение с задержанной оценкой, и функция будет вычисляться при каждом вызове.

Важное отличие от оператора = (который используется для немедленного присваивания значений) состоит в том, что := откладывает вычисление до момента вызова функции. Например:

g[x_] = x^2

В этом случае g[x_] будет присваиваться значению x^2 сразу, а не как функция. Это может привести к нежелательным результатам, если вы ожидаете поведение функции с отложенной оценкой.

Также можно использовать несколько аргументов и более сложные выражения в теле функции. Например:

h[x_, y_] := x^2 + y^2

Здесь функция h принимает два аргумента и возвращает сумму их квадратов. При вызове функции с конкретными значениями для x и y, например h[3, 4], результатом будет 25.

Функции, определённые с использованием :=, могут быть более гибкими и вычисляться только по мере необходимости. Это полезно в случаях, когда вы хотите использовать переменные, которые могут изменяться в процессе работы программы или когда вычисления требуют значительных ресурсов.

Важно помнить, что при каждом вызове функции с разными аргументами Wolfram Mathematica будет вычислять выражение заново, что отличается от операций с немедленным вычислением, как в случае =.

Использование именованных аргументов в функциях

В Wolfram Mathematica можно создавать функции, которые принимают именованные аргументы, что значительно упрощает работу с несколькими параметрами, улучшает читаемость кода и позволяет гибко управлять значениями параметров.

Именованные аргументы объявляются с использованием структуры правил (Rule) в функции. Правила позволяют передавать значения конкретным параметрам, независимо от их порядка в списке аргументов. Это особенно полезно, когда функция имеет много параметров или когда их комбинации могут быть различными для разных вызовов.

Пример простейшей функции с именованными аргументами:

f[x_, y_: 1, z_: 2] := x + y + z

• x_ – обязательный аргумент.
• y_: 1 и z_: 2 – именованные аргументы с значениями по умолчанию. Если эти параметры не переданы, они будут равны 1 и 2 соответственно.

Для вызова функции можно передавать аргументы как по порядку, так и с указанием их имен:

f[3]        (* Результат: 3 + 1 + 2 = 6 *)
f[3, y -> 5] (* Результат: 3 + 5 + 2 = 10 *)
f[3, z -> 4, y -> 5] (* Результат: 3 + 5 + 4 = 12 *)

Когда значения передаются через именованные аргументы, они могут быть указаны в любом порядке, что позволяет повысить гибкость использования функций и избежать ошибок, связанных с неправильным порядком аргументов.

Рекомендации по использованию именованных аргументов

• Используйте именованные аргументы для функций с большим количеством параметров, чтобы повысить читаемость кода и предотвратить путаницу с порядком аргументов.
• Именованные аргументы полезны при разработке функций, которые принимают параметры, значения которых могут изменяться в зависимости от контекста, но не требуют изменения всех аргументов.
• Применяйте правила для значений по умолчанию, чтобы снизить количество повторяющихся вызовов с одинаковыми параметрами.

Чтобы обеспечить более удобное использование именованных аргументов, можно также использовать проверку наличия значений для конкретных параметров:

f[x_, opts:OptionsPattern[]] := Module[{y, z},
y = OptionValue[opts, y, 1];
z = OptionValue[opts, z, 2];
x + y + z
]

• OptionsPattern[] позволяет функции принимать аргументы в виде списка опций.
• OptionValue[opts, y, 1] извлекает значение для параметра y, если оно передано, или использует значение по умолчанию (1), если не передано.

Этот подход позволяет создавать более сложные функции с гибкими параметрами и значительно улучшает управление аргументами в большом коде.

Работа с несколькими аргументами в функции

В Wolfram Mathematica можно создавать функции с несколькими аргументами, что значительно расширяет возможности для решения различных задач. Для этого используется стандартный синтаксис, который позволяет указывать несколько переменных, разделённых запятой.

Пример функции с двумя аргументами:

f[x_, y_] := x^2 + y^2

В этом примере функция f принимает два аргумента x и y. Символ подчеркивания (_) указывает, что это переменные, а не конкретные значения. Такие функции могут быть использованы для вычислений с несколькими входными параметрами, например, для определения суммы квадратов двух чисел.

Для вызова функции с несколькими аргументами нужно передать значения для всех переменных, например:

f[3, 4]

Результат выполнения этого выражения будет равен 25, так как f[3, 4] интерпретируется как 3^2 + 4^2 = 9 + 16 = 25.

Если необходимо задать функцию с произвольным количеством аргументов, можно использовать список аргументов. Например:

g[args__] := Total[args]

Здесь используется специальный символ __ (двойное подчеркивание), который позволяет функции принимать любое количество аргументов. В приведённом примере g суммирует все переданные значения, независимо от их количества.

Пример вызова:

g[1, 2, 3, 4, 5]

Результат: 15, так как функция суммирует все аргументы.

Для работы с аргументами также можно использовать именованные параметры. Например:

h[x_, y_, z_: 10] := x + y + z

Здесь z имеет значение по умолчанию, равное 10. Если значение для z не передано, используется это значение. Например:

h[2, 3]

Результат: 15, так как h[2, 3] интерпретируется как 2 + 3 + 10.

При работе с несколькими аргументами важно помнить о порядке их передачи. Mathematica строго соблюдает порядок аргументов, и это может повлиять на вычисления. Если порядок важен, используйте именованные параметры или списки для улучшения читаемости кода.

Определение функций с ограничениями на аргументы

В Wolfram Mathematica можно задать функцию с ограничениями на её аргументы, используя встроенные механизмы, такие как `ConditionalExpression` или `Which`. Эти конструкции позволяют ограничить область определения функции, указывая допустимые значения для её аргументов. Такие ограничения могут быть полезны для анализа функции в определённой области или при вычислениях с учётом специфических условий.

Для задания функции с ограничениями через `ConditionalExpression` используется следующая структура:

f[x_] := ConditionalExpression[выражение, условие]

Здесь `выражение` – это сама функция, а `условие` – это логическое ограничение для её аргумента. Например, для функции, определённой на интервале [0, 10], можно записать:

f[x_] := ConditionalExpression[x^2, 0 <= x <= 10]

Эта функция будет возвращать \( x^2 \) только для значений \( x \) в пределах от 0 до 10, а для остальных значений она не будет определена.

Кроме того, можно комбинировать несколько ограничений с помощью логических операторов. Например, для функции, которая действует на положительные значения \( x \), но меньше 5, запись будет выглядеть так:

f[x_] := ConditionalExpression[Sin[x], 0 < x < 5]

Если для аргумента \( x \) не выполнено условие, Mathematica вернёт специальное значение `ConditionalExpression[Sin[x], False]`, что свидетельствует о невозможности вычисления функции для этих значений.

Для более сложных условий, когда необходимо указать несколько возможных значений для аргументов, можно использовать конструкцию `Which`, которая позволяет задать несколько логических выражений:

f[x_] := Which[
x < 0, x^2,
x == 0, 1,
x > 0, Sqrt[x]
]

Здесь функция \( f(x) \) возвращает \( x^2 \), если \( x < 0 \), значение 1, если \( x = 0 \), и \( \sqrt{x} \), если \( x > 0 \). Использование `Which` удобно, когда нужно обрабатывать различные интервалы значений для аргумента и возвращать разные выражения в зависимости от этих интервалов.

Важно помнить, что в случае с `ConditionalExpression` можно задать более точные ограничения на аргументы, включая использование нелинейных условий или комплексных выражений. Например, для функции с условием, где аргумент \( x \) должен быть не только больше нуля, но и меньше значения функции \( \sin(x) \), можно написать:

f[x_] := ConditionalExpression[Exp[x], 0 < x < Sin[x]]

Таким образом, Mathematica предоставляет гибкие и мощные инструменты для определения функций с ограничениями, что открывает возможности для более точных математических моделей и анализа.

Отладка функций с помощью отладчика Mathematica

В Mathematica отладка кода функций осуществляется через встроенный отладчик, который позволяет эффективно искать ошибки и отслеживать выполнение программ. Для включения отладчика используется команда Debug, которая активирует пошаговое выполнение функции.

Для начала работы с отладчиком необходимо использовать команду SetDebug[имя_функции], которая ставит точку останова в начало функции. После этого, при вызове функции, выполнение остановится на первой строке, и вы сможете исследовать текущие значения переменных. Для того чтобы пошагово продолжить выполнение, используется команда Step.

Если нужно отслеживать выполнение в пределах нескольких уровней вложенности, можно использовать команду StepOut, которая завершает текущий уровень отладки и продолжает выполнение функции на следующем уровне. Для более точного контроля можно установить точку останова на определённой строке с помощью SetDebug[имя_функции, {строка_кода}].

Кроме того, Mathematica предоставляет функционал для установки нескольких точек останова с различными условиями срабатывания, используя команду Break. Это позволяет значительно сократить время отладки, сосредоточив внимание только на ключевых этапах выполнения программы.

Для более сложных случаев и оптимизации работы отладчика можно использовать команду ClearAll, которая очищает все определения переменных и функций, что полезно для начала нового сеанса отладки без остаточных данных.

По завершении отладки, для удаления всех точек останова, следует использовать команду UnsetDebug, что восстановит обычное выполнение программы без остановок.

Использование встроенных функций в пользовательских функциях

В Wolfram Mathematica встроенные функции играют ключевую роль при создании пользовательских функций. Использование этих функций позволяет эффективно решать задачи и сокращать количество кода. Важно понимать, как интегрировать их в собственные функции, чтобы обеспечить гибкость и производительность программ.

При написании пользовательских функций вы можете комбинировать стандартные функции с собственными алгоритмами. Например, такие функции, как Sin, Cos, Exp, Max и многие другие, могут быть использованы для выполнения математических операций внутри пользовательских функций.

Основные принципы использования встроенных функций:

• Передавайте данные в стандартные функции как аргументы, используя их типы и формат. Например, функция Sin принимает числовые значения, а Max – список или несколько значений.
• Старайтесь использовать встроенные функции для операций, которые уже оптимизированы в Mathematica. Это повысит скорость работы и уменьшит вероятность ошибок.
• Встроенные функции могут быть использованы как в чистых вычислениях, так и в условиях внутри операторов, например в If, Which или Switch.

Пример пользовательской функции с использованием встроенных функций:

f[x_] := If[x > 0, Sin[x], Exp[-x]]

В этом примере функция f использует встроенные функции Sin и Exp для выполнения различных операций в зависимости от значения переменной x.

Можно комбинировать несколько встроенных функций для создания более сложных вычислений. Например, можно использовать Min и Max для нахождения минимального и максимального значений в списке:

g[list_] := Max[Min[list], 0]

Встроенные функции также могут быть полезны для преобразования данных. Например, List, Flatten, Transpose и другие функции помогают манипулировать списками и массивами, что часто требуется в задачах обработки данных.

При создании более сложных функций с использованием встроенных методов, не забывайте про документацию Wolfram Mathematica. Встроенные функции часто имеют дополнительные параметры и опции, которые могут быть полезны для настройки поведения функции в зависимости от контекста.

Кроме того, использование встроенных функций помогает сохранить читабельность кода и ускоряет его выполнение, так как эти функции оптимизированы для работы на уровне ядра Mathematica.

Оптимизация работы функций в Mathematica для больших данных

Для работы с большими объемами данных в Mathematica важна не только правильная реализация функций, но и их эффективная оптимизация. Применение нескольких стратегий позволяет значительно ускорить вычисления и снизить потребление памяти. Рассмотрим основные подходы к оптимизации.

1. Использование встроенных функций вместо собственных алгоритмов. Mathematica содержит большое количество высоко оптимизированных встроенных функций, которые могут выполнить задачи быстрее, чем самописные решения. Например, для операций с массивами данных лучше использовать функции типа `Map`, `Fold` и `Gather`, чем традиционные циклы `For` или `While`.

2. Параллелизация вычислений. Мощности многозадачных процессоров можно эффективно использовать с помощью функций `ParallelMap`, `ParallelTable` и `Parallelize`. Эти инструменты позволяют распределить вычисления между несколькими ядрами процессора, значительно ускоряя выполнение задач.

3. Использование эффективных структур данных. В Mathematica поддерживаются различные структуры данных, такие как ассоциативные массивы (`Association`), матрицы и списки. Выбор правильной структуры для хранения данных помогает ускорить доступ к элементам. Например, для быстрых операций поиска и модификации лучше использовать `Association`, а для обработки больших числовых массивов – `SparseArray` или `MatrixForm`.

4. Избежание многократных вычислений. Если одна и та же операция выполняется несколько раз, можно сохранить её результат с помощью переменной или использовать кеширование. Использование `Memoization` через `SetDelayed` помогает избегать повторных вычислений одинаковых выражений. Пример: при вычислении значения функции для одинаковых входных данных с помощью `f[x_] := f[x] = ...` можно сохранить результат первого вычисления и использовать его в будущем.

5. Использование низкоуровневых функций. В Mathematica можно напрямую обращаться к низкоуровневым функциям, таким как `Compile`, для создания оптимизированных вычислительных операций, которые работают быстрее, чем интерпретируемые. Компиляция позволяет ускорить выполнение функций, особенно если они используют массивы чисел.

6. Распараллеливание больших наборов данных с помощью `Dataset`. Для работы с табличными данными следует использовать объект `Dataset`, который позволяет эффективно фильтровать, трансформировать и агрегировать данные с минимальными затратами памяти. Методы `Dataset` эффективно поддерживают параллельную обработку и могут быть использованы для обработки больших объемов данных.

7. Применение подходов к снижению объема данных. При обработке больших данных имеет смысл уменьшать их объем за счет фильтрации или агрегации перед основной обработкой. Использование методов фильтрации, таких как `Select` или `Pick`, позволяет работать только с необходимыми данными, что снижает нагрузку на систему.

8. Профилирование кода. Для выявления узких мест в производительности используйте инструмент `AbsoluteTiming` или `Timing`, чтобы измерить время работы отдельных частей кода. Инструмент `Profiler` позволяет проанализировать весь процесс вычислений, выявить долгие операции и оптимизировать их.

9. Использование численных методов. Если задача допускает приближенные решения, следует использовать численные методы, такие как `FindRoot`, `NIntegrate`, которые могут выполнять задачи быстрее, чем аналитические методы. Это особенно важно при обработке данных, которые содержат ошибки или шум.

Применяя эти стратегии, можно значительно ускорить выполнение задач с большими данными в Mathematica, снижая время обработки и уменьшая потребление ресурсов. Правильный подход к оптимизации позволяет эффективно работать даже с гигантскими наборами данных, обеспечивая стабильную и быструю работу программы.

Вопрос-ответ:

Что такое функция в Wolfram Mathematica и как ее создать?

В Wolfram Mathematica функция — это блок кода, который выполняет определенную задачу, принимая входные данные и возвращая результат. Чтобы создать функцию, необходимо использовать синтаксис `f[x_] := выражение`, где `f` — это имя функции, `x_` — параметр, а `выражение` — то, что будет вычисляться. Например, для создания функции, которая возвращает квадрат числа, можно написать: `f[x_] := x^2`. Теперь, при вызове `f[3]`, Mathematica вернет 9.

Как задать несколько аргументов функции в Wolfram Mathematica?

Чтобы задать несколько аргументов, нужно просто перечислить их через запятую внутри квадратных скобок. Например, если требуется создать функцию, которая принимает два аргумента и складывает их, можно написать: `f[x_, y_] := x + y`. При вызове `f[2, 3]` результатом будет 5. Важно заметить, что каждый аргумент в определении функции помечается символом подчеркивания, как в `x_` и `y_`.

Какие особенности есть у локальных и глобальных переменных при создании функции в Mathematica?

При создании функции в Wolfram Mathematica важно различать локальные и глобальные переменные. Локальная переменная определяется с использованием подчеркивания, как `x_`, и она существует только в контексте данной функции. Глобальная переменная, напротив, используется за пределами функции и сохраняет значение между вызовами. Например, если переменная `a` определена вне функции, то изменение ее значения внутри функции не повлияет на глобальную переменную. Однако, если вы хотите использовать глобальную переменную внутри функции, ее значение нужно явно передать.

Как работает отладка функции в Wolfram Mathematica?

Для отладки функции в Mathematica можно использовать встроенные инструменты, такие как `Trace` и `Print`. Команда `Trace` позволяет отслеживать выполнение выражений, а `Print` — выводить промежуточные результаты в процессе работы функции. Например, добавив `Print[x]` в тело функции, вы сможете видеть, какие значения принимает параметр `x` при каждом вызове. Также полезным инструментом является `Check`, который позволяет ловить ошибки выполнения функции.

Можно ли использовать условные операторы внутри функций в Wolfram Mathematica?

Да, в Wolfram Mathematica можно использовать условные операторы внутри функций. Для этого применяется конструкция `If`. Например, можно создать функцию, которая возвращает "Четное", если число четное, и "Нечетное", если число нечетное. Это можно сделать так: `f[x_] := If[Mod[x, 2] == 0, "Четное", "Нечетное"]`. Когда вы вызываете `f[4]`, результатом будет "Четное". Также существует конструкция `Which`, которая позволяет проверять несколько условий по очереди.