Как задать кусочную функцию в maple

В Maple кусочные функции задаются с использованием конструкции piecewise. Эта команда позволяет определить функцию, принимающую различные выражения в зависимости от условий на область определения. Синтаксис: piecewise(условие1, выражение1, условие2, выражение2, ..., выражение_по_умолчанию). Каждый блок условия и соответствующего выражения указывается последовательно, после чего можно задать выражение по умолчанию, которое используется, если ни одно из условий не выполнено.

При определении кусочной функции критически важно правильно задать логические условия. Maple поддерживает операторы <, <=, >, >=, =, <> и логические связки and, or, not. Например, функция, принимающая значение x при x < 0 и значение x^2 при x ≥ 0, задаётся как piecewise(x < 0, x, x >= 0, x^2).

Для последующего анализа или визуализации функции в Maple её лучше присвоить переменной, например: f := x -> piecewise(x < -1, -1, x <= 1, x, 1). Это упростит использование функции в командах plot, diff, int и других. Важно также учитывать, что при дифференцировании или интегрировании кусочной функции Maple автоматически учитывает границы, где функция меняет поведение.

Если необходимо задать сложную комбинацию условий или использовать параметры, рекомендуется определить условия и выражения заранее в отдельных переменных. Это облегчает отладку и делает структуру piecewise-функции более читаемой. Например: cond1 := x < a: cond2 := x >= a and x <= b: expr := piecewise(cond1, f1(x), cond2, f2(x), f3(x)).

Синтаксис оператора piecewise в Maple

Оператор piecewise в Maple задаёт кусочную функцию с явным указанием условий и соответствующих выражений. Базовая структура имеет вид:

piecewise(условие1, выражение1, условие2, выражение2, ..., выражение_по_умолчанию)

Каждое условие – это логическое выражение, возвращающее true или false. Если оно истинно, возвращается соответствующее выражение. Проверка условий выполняется последовательно, пока не найдётся первое истинное. Если ни одно из условий не выполняется, используется последнее выражение – значение по умолчанию.

Пример: f := x -> piecewise(x < 0, -x, x <= 1, x^2, 2) определяет функцию, равную -x при x < 0, x² при 0 ≤ x ≤ 1 и 2 во всех остальных случаях.

Условия можно комбинировать с помощью логических операторов: and, or, not. Например: piecewise(x >= -1 and x < 1, sin(x), 0).

Оператор поддерживает символьные и численные вычисления. Для символьных переменных важно использовать assume или assuming при необходимости уточнить область значений, так как без этого Maple может не интерпретировать условие как однозначно истинное или ложное.

Чтобы избежать неоднозначностей, исключай перекрывающиеся условия. Например, piecewise(x < 2, x+1, x < 5, x^2, x) может вернуть неожиданные результаты при x < 2, так как это также удовлетворяет x < 5. Упорядочивай условия от наиболее строгих к общим.

Создание кусочной функции с числовыми условиями

Для определения кусочной функции с числовыми границами в Maple используется оператор piecewise. Синтаксис: piecewise(условие1, выражение1, условие2, выражение2, ..., выражение_по_умолчанию).

Пример: задать функцию f(x), равную 2x при x < -1, x² при -1 ≤ x < 3, и 5 при x ≥ 3:

f := x -> piecewise(x < -1, 2*x, x < 3, x^2, 5);

Maple интерпретирует условия последовательно. Важно избегать пересечений и неполных областей. В приведённом примере условие x < 3 охватывает промежуток от -1 включительно до 3, так как x < -1 уже описан первым условием.

Для проверки корректности определения используйте plot(f(x), x = -5..5);. Это позволит визуально убедиться в правильности переходов между участками.

Если необходимо использовать строгое равенство в точке, задавайте его явно: piecewise(x = 0, 1, x < 0, -1, 2) – функция равна 1 при x = 0, -1 при x < 0 и 2 во всех остальных случаях.

При необходимости использовать вещественные интервалы с высокой точностью, избегайте логических ошибок при работе с неравенствами. Например, вместо -1 <= x < 3 используйте x >= -1 and x < 3.

Определение кусочной функции с параметрами

В Maple для задания кусочной функции с параметрами целесообразно использовать конструкцию piecewise. Это позволяет задать функцию, значение которой зависит как от области определения переменной, так и от дополнительных параметров.

Пример определения функции f(x, a), зависящей от параметра a:

f := (x, a) -> piecewise(x < 0, a*x^2, x >= 0 and x < 1, sin(a*x), x >= 1, a + x);

В этом выражении функция принимает различные формулы в зависимости от значения переменной x, а параметр a может быть произвольным числом. Maple корректно интерпретирует такие определения, позволяя впоследствии выполнять подстановку, дифференцирование и интегрирование по x и a.

Для визуализации функции с фиксированным значением параметра используйте:

plot(f(x, 2), x = -2..2);

Чтобы проанализировать поведение функции при различных значениях параметра, удобно применять plots[animate]:

with(plots): animate(plot, [f(x, a), x = -2..2], a = 1..5);

Кусочные функции с параметрами можно использовать внутри систем уравнений, при численном решении задач и в символьных преобразованиях. Следует избегать неоднозначных условий и перекрытия областей определения – это вызывает предупреждения и может привести к ошибкам вычислений.

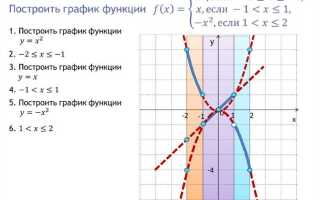
Графическое отображение кусочной функции

Для визуализации кусочной функции в Maple используйте команду plot с функцией, определённой через piecewise. Пример:

f := x -> piecewise(x < 0, -1, x <= 2, x^2, 3);
plot(f(x), x = -2 .. 4);

Если необходимо отобразить разрывы или точки перехода, добавьте параметр discont = true:

plot(f(x), x = -2 .. 4, discont = true);

Для контроля над цветами, толщиной линий и стилем используйте опции color, thickness, linestyle. Например:

plot(f(x), x = -2 .. 4, discont = true, color = red, thickness = 2, linestyle = dash);

Чтобы отобразить отдельные куски с разными параметрами, используйте plots[display] и plot для каждого отрезка:

with(plots):
p1 := plot(-1, x = -2 .. 0, color = blue):
p2 := plot(x^2, x = 0 .. 2, color = green):
p3 := plot(3, x = 2 .. 4, color = red):
display([p1, p2, p3]);

Для отображения открытых и закрытых точек используйте plottools[disk] и plottools[point]. Пример добавления открытой точки в x=0:

openDot := plottools[disk]([0, -1], 0.07, color = white):
display([p1, p2, p3, openDot]);

Для автоматизации построения и добавления всех деталей рекомендуется объединять графики в списки и использовать display для компоновки итогового изображения.

Подстановка значений в кусочную функцию

В Maple для подстановки значения в кусочную функцию необходимо использовать оператор subs или непосредственное обращение к функции с аргументом. Однако, в случае кусочной (piecewise) функции, важно учитывать диапазоны определения каждого участка.

• Если функция задана с помощью piecewise, например:
  f := x -> piecewise(x < 0, x^2, x <= 5, x + 1, 2*x);
  то подстановка значения производится так:
  f(-2); вернёт 4, f(3); – 4, f(6); – 12.
• При программной подстановке используется subs:
  subs(x=3, f(x)); – результат будет эквивалентен f(3);.
• Если кусочная функция встроена в выражение, подстановку следует выполнять последовательно:
  1. Подставить значение переменной через subs.
  2. Упростить результат с помощью simplify или eval, если subs оставил неопределённость.
• Для массивной подстановки удобно использовать map:
  map(f, [-2, 0, 5, 6]); – вернёт список значений функции для каждого аргумента.
• Важно: если значение аргумента не попадает ни в один из диапазонов, будет возвращено последнее выражение в piecewise. Убедитесь, что охвачен весь диапазон возможных значений.

Дифференцирование и интегрирование кусочной функции

Для выполнения дифференцирования и интегрирования кусочной функции в Maple необходимо учитывать особенности её определения на различных промежутках.

• Дифференцирование реализуется через оператор diff, применяемый к каждой части функции отдельно. Важно явно задать область действия каждой ветви.
• В Maple можно использовать конструкцию piecewise, где для каждого интервала задаётся своя формула. Дифференцирование отработает корректно на каждом участке, возвращая выражения для соответствующих интервалов.
• Особое внимание уделите точкам разрыва функции или её производной – Maple по умолчанию не обрабатывает поведение в точках смены ветвей, что требует дополнительного анализа.

Интегрирование кусочной функции удобно выполнять по частям, используя встроенный оператор int с ограничением области интегрирования:

• Для интеграла по всему интервалу функции разбейте задачу на сумму интегралов по каждому подынтервалу, соответствующему ветвям кусочной функции.
• Maple корректно вычисляет неопределённый интеграл от выражения, определённого для конкретного подинтервала, но не суммирует результаты автоматически.
• Если нужно получить определённый интеграл, указывайте пределы интегрирования строго в рамках каждой ветви, затем складывайте результаты.

Рекомендуется:

1. Перед дифференцированием и интегрированием проверять корректность определения функции через piecewise, избегая перекрытий и пропусков в интервалах.
2. Использовать функции limit и eval для исследования поведения на границах кусочных участков.
3. В сложных случаях строить графики с помощью plot и plots:-piecewiseplot для визуальной проверки результатов.

Вопрос-ответ:

Как в Maple определить функцию, состоящую из нескольких кусочков с разными правилами на разных интервалах?

В Maple можно создать такую функцию с помощью команды piecewise. В качестве аргументов указываются условия на переменную и соответствующие выражения. Например, piecewise(x < 0, x^2, x >= 0, x + 1) задаст функцию, равную x² при x меньше 0 и x+1 при x не меньше 0.

Можно ли в Maple задать кусочную функцию с более чем двумя частями, и как это сделать?

Да, Maple поддерживает функции с любым числом частей. Для этого в команде piecewise перечисляются пары условий и выражений. Каждое условие описывает интервал, а после него указывается формула для этого участка. Например, piecewise(x < -1, 0, x >= -1 and x < 2, x^2, x >= 2, 5) создаст функцию из трех кусочков.

Как работать с кусочной функцией в Maple, если нужно найти её значение в конкретной точке?

Для вычисления значения функции в Maple достаточно подставить число вместо переменной. Например, если f := piecewise(x < 0, x^2, x >= 0, x + 1), то f(2) вернёт 3, а f(-1) — 1. Maple автоматически определит, к какому интервалу относится значение аргумента и применит соответствующее выражение.

Можно ли использовать кусочную функцию Maple для построения графиков, и есть ли особенности при этом?

Да, функции, заданные с помощью piecewise, легко отображаются на графиках. При построении графика команда plot корректно обрабатывает разные участки функции, переходы между ними. Однако если переходы имеют разрывы, график покажет их чётко. Для более сложных случаев можно использовать дополнительные параметры построения.

Как задать кусочную функцию с параметрами в Maple, чтобы менять формулы внутри без пересоздания функции?

В Maple можно определить параметрическую кусочную функцию, объявив параметры отдельно, например, через assign, а затем использовать их внутри piecewise. Например, если задать a := 2, b := 3, то piecewise(x < 0, a*x, x >= 0, b*x^2) будет использовать текущие значения a и b. Изменяя параметры, можно менять форму функции без её повторного определения.

Как задать кусочную функцию в Maple для разных промежутков значений?

В Maple можно определить кусочную функцию с помощью конструкции `piecewise`. Для каждого интервала задается условие и соответствующее значение функции. Например, запись `piecewise(x<0, -1, x=0, 0, x>0, 1)` задает функцию, которая принимает значение -1 при x меньше нуля, 0 при x равном нулю и 1 при x больше нуля. Такая форма позволяет чётко описать поведение функции на разных частях области определения.

Какие типичные ошибки возникают при работе с кусочными функциями в Maple и как их избежать?

Часто встречающаяся ошибка — неправильное указание условий в функции `piecewise`, например, пересекающиеся или неполные области. Это может привести к некорректным результатам вычислений. Чтобы избежать таких проблем, следует внимательно прописывать условия так, чтобы они покрывали всю область определения без перекрытий. Также полезно проверять функцию с разными значениями аргумента, чтобы убедиться, что Maple правильно выбирает нужный участок. Иногда возникают сложности с упрощением выражений, в этом случае можно использовать функции упрощения или подставлять конкретные значения для проверки.