Передаточная функция в MATLAB задаётся с использованием встроенной функции tf, которая позволяет описать линейную стационарную систему во временной или частотной области. Основной формат записи: tf(num, den), где num и den – векторы коэффициентов числителя и знаменателя соответственно. Например, для системы с передаточной функцией (2s + 5)/(s² + 3s + 2) используется выражение: tf([2 5], [1 3 2]).
Для задания систем с запаздыванием необходимо использовать аргумент ‘InputDelay’. Пример: tf([1], [1 2], ‘InputDelay’, 0.5) создаёт передаточную функцию с задержкой 0.5 секунды. При этом MATLAB автоматически учитывает влияние запаздывания на устойчивость и частотные характеристики модели.
Если требуется задать несколько передаточных функций одновременно, удобно использовать массивы систем. Например: G = tf({[1], [2]}, {[1 1], [1 2]}) создаёт матрицу передаточных функций, каждая из которых имеет собственный числитель и знаменатель. Это особенно полезно при моделировании многоканальных систем управления.
Для повышения точности моделирования предпочтительно использовать нормализацию коэффициентов, особенно при работе с высокими порядками полиномов. Использование функции zpk для задания нулей, полюсов и коэффициента усиления даёт более устойчивое представление в случаях, когда числитель и знаменатель имеют общие корни: zpk([-2], [-1 -3], 4).
Создание передаточной функции с помощью команды tf
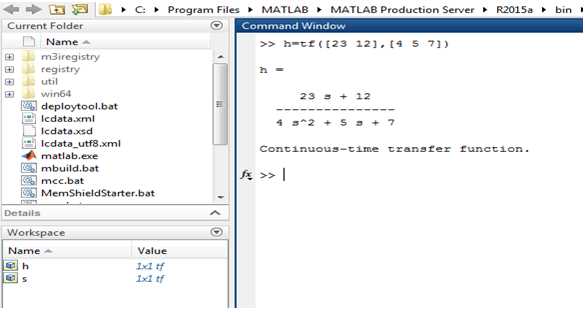
Для задания передаточной функции в MATLAB применяют команду tf, которая формирует объект модели линейной системы в виде дробно-рационального выражения от переменной s.
- Синтаксис:
sys = tf(num, den), гдеnum– вектор или массив коэффициентов числителя,den– вектор или массив коэффициентов знаменателя. - Пример:
tf([5 3], [1 4 6])создаёт систему с передаточной функцией \( \frac{5s + 3}{s^2 + 4s + 6} \). - Для задания нескольких входов и выходов используют массивы. Пример:
tf({[1], [2 1]; [0], [3]}, {[1 2], [1 3]; [1 4], [1 5]}).
Порядок коэффициентов – от старших к младшим степеням переменной s. При несоответствии размерностей числителя и знаменателя необходимо дополнить вектор нулями.
- Перед использованием рекомендуется нормализовать коэффициенты, чтобы исключить ошибки округления при численных вычислениях.
- Проверяйте порядок системы:
order(sys)возвращает степень знаменателя. - Для получения нулей, полюсов и коэффициента усиления используйте:
zpk(sys).
Для дискретных систем дополнительно указывают время дискретизации: tf(num, den, Ts), где Ts – положительное число.
Задание числителя и знаменателя в виде векторов
В MATLAB передаточная функция системы представляется с помощью объектов типа tf. Основой такого задания служат векторы коэффициентов числителя и знаменателя, записанные по убыванию степеней переменной s.
- Числитель указывается как массив коэффициентов при s. Например, для 2s² + 3s + 5 – вектор
[2 3 5]. - Знаменатель вводится аналогично. Для s³ + 4s² + 6s + 1 –
[1 4 6 1].
Создание передаточной функции:
num = [2 3 5]; % числитель
den = [1 4 6 1]; % знаменатель
G = tf(num, den);Важно:
- Количество элементов в каждом векторе определяет порядок соответствующего полинома. Нулевые коэффициенты обязательно включать. Например, 3s² + 0s + 7 –
[3 0 7]. - Коэффициенты должны быть вещественными числами. Комплексные значения допустимы, но используются крайне редко.
- Если порядок числителя ниже порядка знаменателя, MATLAB автоматически добавит нули в начало числителя для выравнивания размеров при необходимости.
Для многочастотных систем с несколькими передаточными функциями можно использовать матрицы:
num = {[1 0], [2 3]}; % два числителя
den = {[1 2 1], [1 0 4]}; % два знаменателя
G = tf(num, den);Векторы должны быть синхронизированы по структуре: каждый числитель должен соответствовать своему знаменателю по позиции в ячейковом массиве.
Использование полиномиальных и символьных выражений
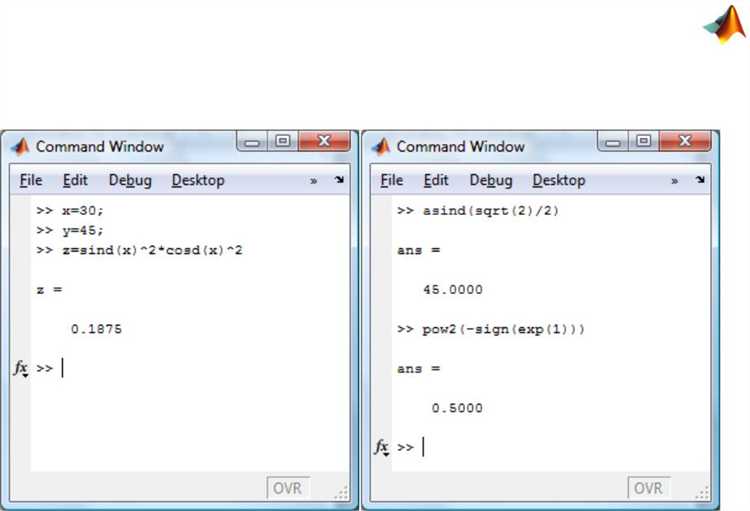
Для задания передаточной функции в MATLAB можно использовать полиномиальные коэффициенты и символьные выражения. Полиномиальный подход основывается на задании числителя и знаменателя функции в виде векторов, содержащих коэффициенты при степенях переменной s. Например, передаточная функция H(s) = (2s + 5)/(s^2 + 3s + 2) задаётся как:
num = [2 5];
den = [1 3 2];
H = tf(num, den);
Важно соблюдать порядок убывания степеней: первый элемент массива соответствует старшей степени. Отсутствие промежуточного коэффициента заменяется нулём. Пример: для s² + 0·s + 1 следует писать [1 0 1].
Символьные выражения позволяют оперировать с передаточными функциями аналитически. Используется пакет Symbolic Math Toolbox. Определение переменной и функции:
syms s;
H_sym = (2*s + 5)/(s^2 + 3*s + 2);
Для преобразования символьного выражения в объект tf требуется использование функции sym2poly:
num = sym2poly(numerator(H_sym));
den = sym2poly(denominator(H_sym));
H_tf = tf(num, den);
Символьный подход удобен при выполнении алгебраических преобразований: упрощение, разложение, нахождение корней. Однако при переходе к численным расчётам рекомендуется конвертация в полиномиальную форму, чтобы обеспечить совместимость с функциями управления и моделирования.
Работа с передаточными функциями с задержкой
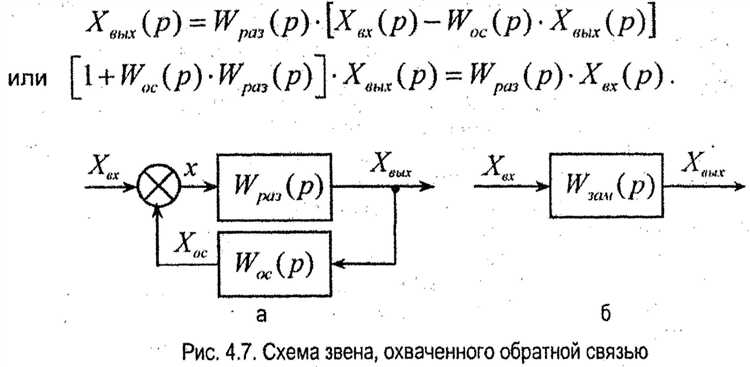
В MATLAB для моделирования систем с запаздыванием используется класс tf с параметром задержки 'InputDelay', 'OutputDelay' или 'ioDelay'. Например, передаточная функция с числителем [1], знаменателем [1 5] и задержкой 3 секунды задается так:
G = tf(1, [1 5], 'InputDelay', 3);Для передачи запаздывания в экспоненциальной форме (e-sT), допустимо использование:
s = tf('s');
G = exp(-3*s)/(s+5);Такой способ требует переменной s, создаваемой как tf('s'). Однако аналитические методы, такие как обратное преобразование Лапласа или факторизация, при наличии запаздывания могут быть ограничены. Для численного анализа задержку удобно аппроксимировать с помощью приближения Паде:
G = tf(1, [1 5]);
G_delay = pade(G, 3);По умолчанию используется приближение первого порядка. Для повышения точности указывайте порядок явно:
G_delay = pade(G, 3, 4);Задержки сохраняются при арифметических операциях с передаточными функциями, но могут вызвать трудности при символьных преобразованиях или упрощениях. Используйте команду absorbDelay для преобразования задержек в экспоненциальную форму, если требуется экспортировать модель или упростить структуру:
G = tf(1, [1 5], 'InputDelay', 2);
G_exp = absorbDelay(G);При линейном моделировании и использовании функций step, impulse и lsim MATLAB корректно учитывает запаздывание без необходимости аппроксимации. Для устойчивости и частотного анализа задержка влияет на фазовую характеристику, но не на модуль, что важно при использовании bode и margin.
Преобразование между различными представлениями систем

В MATLAB преобразование между передаточной функцией, моделью в пространстве состояний и Z-преобразованием выполняется с помощью строго определённых функций. Для перехода от передаточной функции к пространству состояний применяется команда ss(). Например, sys_ss = ss(sys_tf); преобразует объект sys_tf типа tf в представление state-space.
Обратное преобразование выполняется функцией tf(): sys_tf = tf(sys_ss);. Это необходимо при анализе устойчивости или частотных характеристик, когда удобнее использовать передаточную функцию.
Для перехода к нулевому и полюсно-остаточному представлениям применяются функции zpk() и ss2zp(). Пример: sys_zpk = zpk(sys_tf); преобразует систему в вид нули-полюса-усиление.
Если модель задана в виде матриц A, B, C, D, то их можно напрямую использовать при создании модели в пространстве состояний: sys_ss = ss(A, B, C, D);. При необходимости получить коэффициенты числителя и знаменателя из передаточной функции используют [num, den] = tfdata(sys_tf, 'v');.
При работе с цифровыми системами важно учитывать дискретизацию. Преобразование между непрерывной и дискретной формой выполняется с помощью c2d() и d2c(). Пример: sys_d = c2d(sys_c, Ts, 'zoh'); дискретизирует непрерывную систему методом нулевого порядка с шагом дискретизации Ts.
Все преобразования сохраняют динамику системы при корректном использовании. Однако важно учитывать особенности представления: например, численная устойчивость может ухудшиться при преобразовании между формами при наличии близких нулей и полюсов. Рекомендуется проверять результат через функции bode(), step() или impulse() для сравнения откликов.
Проверка корректности введённой передаточной функции
После задания передаточной функции в MATLAB важно убедиться, что её структура и параметры соответствуют ожидаемым. Для этого используйте команду tf, создавая объект передаточной функции с числителем и знаменателем, переданными в виде векторов коэффициентов. Неправильный ввод, например, пустой или нулевой вектор, вызовет ошибку или некорректное поведение.
Проверьте размерность векторов числителя и знаменателя: они должны содержать хотя бы один коэффициент, причем знаменатель не может быть нулевым полиномом. Для диагностики используйте isproper(sys), которая возвращает true, если порядок числителя не превышает порядок знаменателя. Несоблюдение этого приводит к физически невозможным системам.
Для визуальной проверки можно построить графики импульсной и ступенчатой реакций с помощью функций impulse(sys) и step(sys). Аномалии на этих графиках указывают на ошибки в модели или неверный ввод коэффициентов.
Дополнительно воспользуйтесь функцией pole(sys) для определения полюсов системы. Наличие полюсов в правой половине комплексной плоскости свидетельствует о нестабильности, что часто связано с ошибками при формулировании передаточной функции.
Для автоматической проверки корректности используйте блок try-catch, который отловит ошибки при создании объекта. Например, при передаче некорректных данных MATLAB выдаст сообщение об ошибке, позволяющее скорректировать ввод.
Сохранение и загрузка моделей передаточных функций
Для сохранения передаточной функции в MATLAB применяют команду save, позволяющую сохранить объект в файл формата .mat. Рекомендуется сохранять модели в отдельных переменных, например: save('model.mat', 'sys'), где sys – передаточная функция, созданная с помощью tf или ss.
Для загрузки ранее сохраненной модели используют команду load. При загрузке файл .mat импортирует все сохранённые переменные, что позволяет восстановить объект передаточной функции. Например, load('model.mat') загрузит переменную sys в рабочее пространство.
Для обмена моделями между сессиями и проектами рекомендуется использовать имена файлов с описательными названиями и хранить их в отдельных папках. При работе с несколькими моделями в одном файле сохраняйте их с разными именами переменных, чтобы избежать перезаписи.
Если необходимо передавать модель в текстовом формате, MATLAB поддерживает экспорт в формат LTI- или TF-файлов через команды writeTFM (при наличии соответствующих тулбоксов) или сохранение коэффициентов с помощью save в формате .m, например: save('model_coeffs.m','num','den'). Для восстановления модели затем используйте tf(num, den).
Автоматизация сохранения моделей через скрипты и функции облегчает управление версиями и интеграцию с системами контроля версий. Для быстрого тестирования и визуализации загруженных моделей применяйте команды step, bode и impulse сразу после загрузки.
Вопрос-ответ:
Как в MATLAB задать передаточную функцию с несколькими полюсами и нулями?
Передаточная функция в MATLAB обычно задаётся с помощью команды tf. Чтобы указать несколько полюсов и нулей, нужно передать в tf числитель и знаменатель в виде векторов коэффициентов многочленов. Например, tf([1 3 2], [1 5 6]) создаст передаточную функцию с числителем s² + 3s + 2 и знаменателем s² + 5s + 6.
Можно ли в MATLAB получить передаточную функцию по коэффициентам дифференциального уравнения?
Да, MATLAB позволяет легко получить передаточную функцию из дифференциального уравнения. Для этого коэффициенты уравнения записываются в виде полиномов числителя и знаменателя, затем передаются в команду tf. Например, если уравнение задаётся как a2*y» + a1*y’ + a0*y = b2*u» + b1*u’ + b0*u, то числитель — это вектор [b2 b1 b0], а знаменатель — [a2 a1 a0].
Как проверить корректность созданной передаточной функции в MATLAB?
Чтобы убедиться, что передаточная функция задана правильно, можно использовать команды bode, step или impulse. Они строят частотные характеристики, переходные и импульсные отклики. Если графики выглядят логично и совпадают с ожидаемыми, значит функция задана корректно. Кроме того, можно вывести передаточную функцию на экран командой tf и проверить числитель и знаменатель.
Можно ли задать передаточную функцию с помощью полюсов и нулей, а не коэффициентов многочленов?
Да, в MATLAB существует способ задания передаточной функции через полюса и нули. Для этого используется команда zpk, в которую передаются векторы нулей, полюсов и коэффициент усиления. Например, zpk([zero1 zero2], [pole1 pole2 pole3], gain) создаст модель с указанными характеристиками.
Как преобразовать передаточную функцию в модель состояния в MATLAB?
Преобразовать передаточную функцию в состояние можно с помощью функции ss. Нужно сначала создать объект передаточной функции с помощью tf, а затем применить ss к нему. Это даст модель в пространстве состояний, которая удобна для дальнейшего анализа и управления. Например: sys_tf = tf([1 2], [1 3 2]); sys_ss = ss(sys_tf).
Как в MATLAB задать передаточную функцию с помощью коэффициентов числителя и знаменателя?
Для задания передаточной функции в MATLAB используется команда tf. В качестве аргументов указываются векторы коэффициентов числителя и знаменателя. Например, если числитель — это \(s + 2\), а знаменатель — \(s^2 + 3s + 5\), то их представляют как векторы коэффициентов: числитель [1 2], знаменатель [1 3 5]. Тогда команда будет выглядеть так: sys = tf([1 2], [1 3 5]); После этого переменная sys будет содержать объект передаточной функции, с которым можно работать дальше.
Можно ли задать передаточную функцию в MATLAB в виде дроби с символами, не используя числовые коэффициенты?
Да, в MATLAB есть возможность задавать передаточные функции в символьном виде с помощью пакета Symbolic Math Toolbox. Для этого создают символическую переменную, например s = tf(‘s’); Затем можно записать передаточную функцию как выражение, например, sys = (s + 2)/(s^2 + 3*s + 5); Такой объект также будет восприниматься MATLAB как передаточная функция. Это удобно при необходимости работать с переменными, а не только с конкретными числами, например для аналитических преобразований или построения моделей с параметрами.