Работа с периодическими функциями в Mathcad требует точного понимания синтаксиса и логики платформы. В отличие от других систем компьютерной математики, Mathcad ориентирован на визуальное представление расчетов, поэтому создание корректной периодической зависимости требует четкой структуры выражений и правильного использования управляющих конструкций.
Для задания периодической функции оптимально использовать функции с условием или встроенную функцию mod для реализации цикличности. Например, чтобы определить функцию с периодом T, достаточно описать ее поведение на одном интервале и использовать операцию взятия остатка: f(t) := g(mod(t, T)). Такой подход обеспечивает минимальное количество кода и высокую читаемость формулы.
При необходимости описать кусочно-заданную функцию на одном периоде, следует использовать if-блоки с логическими условиями. Это особенно актуально при построении прямоугольных, треугольных или пилообразных сигналов, где важна точная детализация формы сигнала на интервале. Например, прямоугольная функция с коэффициентом заполнения 0.3 может быть задана как: f(t) := if mod(t, T) < 0.3·T, A, 0.
Для повышения гибкости кода рекомендуется использовать параметризацию: период, амплитуду и фазовый сдвиг выносить в отдельные переменные. Это упрощает модификацию модели и делает функцию пригодной для повторного использования в более сложных расчетах или при численном моделировании.
Определение периода функции с использованием встроенных переменных
В Mathcad для анализа периодических функций удобно использовать переменные T, ω и встроенные средства работы с графиками. Предположим, задана функция f(t) := sin(2·π·t/3). Явно видно, что период равен 3, но Mathcad позволяет проверить это численно.
Создайте диапазон значений: t := 0, 0.01 .. 10. Затем определите функцию f(t) и постройте график. Выявление повторяющегося паттерна визуально подтверждает период.
Для точной оценки используйте разность аргументов при равных значениях функции: find(t1) и find(t2), где f(t1) = f(t2) и t2 > t1. Используйте оператор root или given–find с условием f(t2) = f(0), t2 ≠ 0. Например:
given
f(t2) = f(0)
t2 > 0
find(t2)
Полученное значение и будет периодом. Для автоматизации можно задать параметр T := t2 и использовать его при построении графика или при расчетах в других выражениях.
Если функция задана параметрически, например g(t) := cos(ω·t), то период T выражается как T := 2·π/ω. В этом случае ω можно задать как переменную и использовать ее для адаптации периода без пересчета функции.
Проверка осуществляется сравнением g(t) = g(t + T) на выбранном интервале. При необходимости примените численную подстановку и округление до нужной точности с помощью round или approx.
Создание периодической функции через оператор if
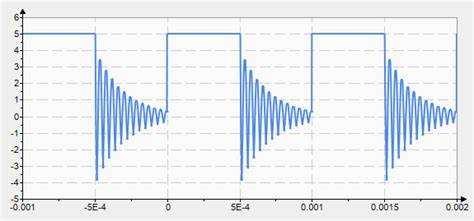
Для построения периодической функции в Mathcad с использованием оператора if, необходимо вручную задать условия для каждого участка периода. Это особенно полезно при создании кусочно-заданных функций.
- Определите длину периода
T. Например:T := 2 - Вычислите значение аргумента внутри одного периода:
x_mod := x - T * floor(x / T) - Используйте вложенные
if-выражения для определения значения функции на каждом интервале периода.
Пример: построение периодической прямоугольной функции с периодом 2, принимающей значения 1 на интервале [0,1) и -1 на [1,2):
T := 2
x_mod(x) := x - T * floor(x / T)
f(x) := if x_mod(x) < 1 then 1 else -1
x_mod(x)гарантирует, что аргумент функции всегда попадает в диапазон одного периода.- Функция
floorустраняет дробную часть при делении на период, обеспечивая цикличность. - Можно расширить конструкцию с
ifдо любой формы сигнала: треугольной, пилообразной, ступенчатой.
Важно: вложенность if затрудняет чтение кода при большом числе интервалов. Для сложных функций используйте определение через массивы и векторы вместо многочисленных условий.
Использование модуля для задания периодичности
В Mathcad для задания периодической функции эффективно применяется оператор модуля – mod(). Он позволяет сформировать функцию, повторяющуюся через заданный интервал, без необходимости вручную описывать каждый период. Это особенно полезно при работе с кусочно-заданными функциями.
Пример: необходимо задать прямоугольную функцию f(t) с периодом T = 4 и значениями 1 на интервале [0;2), 0 – на [2;4). Сначала определим вспомогательную переменную: t_mod := mod(t, 4). Далее используем условный оператор: f(t) := if t_mod < 2 then 1 else 0. Такая конструкция автоматически повторяет шаблон по всей области определения функции.
При работе с модулями следует учитывать, что mod(a, b) возвращает остаток от деления a на b, имеющий тот же знак, что и делимое. Это важно при отрицательных значениях аргумента. Чтобы обеспечить симметричное поведение функции относительно нуля, используйте выражение: mod(t, T) или mod(t + T, T), в зависимости от требуемого смещения.
Модуль особенно полезен при аппроксимации сигналов, построении пользовательских функций для моделирования импульсных процессов или реализации периодических граничных условий в расчетах. Использование mod() делает описание функций компактным, легко редактируемым и пригодным для масштабирования.
Применение циклических выражений с функцией mod
Функция mod в Mathcad используется для создания периодических выражений за счёт возврата остатка от деления. Это особенно полезно при моделировании функций, поведение которых повторяется через заданный интервал.
Для задания периодической функции с периодом T используется выражение вида: f(x mod T). Например, чтобы создать функцию, повторяющую отрезок синуса на интервале [0, π], задаётся выражение: sin(x mod π). При этом вне зависимости от значения x, аргумент функции остаётся в пределах одного периода.
При построении кусочных периодических функций удобно использовать mod совместно с логическими условиями. Пример: прямоугольный сигнал с периодом 4 и значениями 1 на [0,2), 0 на [2,4) описывается как (x mod 4 < 2) = 1. Это выражение возвращает 1, когда остаток от деления меньше 2, и 0 – в противном случае.
Для сложных форм периодических сигналов рекомендуется использовать вложенные условные конструкции с mod. Например, пилообразный сигнал с периодом T реализуется выражением: f(x) := x mod T, при этом результат линейно возрастает от 0 до T, затем сбрасывается.
Функция mod работает с дробными аргументами. Это позволяет строить непрерывные функции, например, треугольный сигнал: abs((x mod T) - T/2). Здесь создаётся симметричный профиль относительно середины периода.
Использование mod устраняет необходимость вручную повторять выражения на каждом интервале. Это повышает читаемость, упрощает отладку и позволяет легко изменять параметры периода и формы сигнала.
Визуализация периодической функции на графике
Для отображения периодической функции в Mathcad используйте встроенный инструмент Plot. Начните с определения функции с указанием параметров периода, амплитуды и фазы. Например, для синусоиды с периодом 2π и амплитудой 3:
f(t) := 3·sin(t)
Задайте диапазон аргумента с шагом, достаточным для точной отрисовки. Оптимально использовать шаг в 0.01–0.1 в зависимости от частоты сигнала:
t := 0, 0.05..6·π
Для построения графика вызовите 2D Plot и перетащите переменные t и f(t) на соответствующие оси. Для корректного отображения нескольких периодов функции установите диапазон оси X вручную. Например, от 0 до 6π, чтобы визуализировать три полных цикла.
Если функция имеет разрывы или определяется кусочно, используйте оператор if или piecewise при определении. Это особенно важно для функций типа прямоугольного или пилообразного сигнала.
Убедитесь, что масштаб по оси Y отражает амплитуду сигнала. Например, при амплитуде ±3, диапазон должен быть от -3.5 до 3.5 для наглядности. Используйте сетку и аннотации точек экстремума, если требуется анализ формы сигнала.
Для отображения нескольких функций на одном графике, добавляйте их как отдельные кривые в один 2D Plot. Указывайте цвет и стиль линии вручную, чтобы различать графики при сравнении форм или фазовых сдвигов.
Проверка корректности задания периода в расчетах
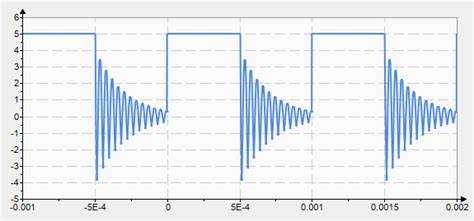
Для обеспечения точности расчетов в Mathcad критично правильно задать период периодической функции. Во-первых, необходимо сверить значение периода с теоретическим определением функции: например, для синуса и косинуса период равен 2π, для функции тангенса – π. Ошибка даже на доли единицы приведет к искажению результатов.
Во-вторых, следует проверить, что период в расчетах задается в тех же единицах измерения, что и аргумент функции. Если аргумент в градусах, период должен быть 360°, в радианах – 2π. Несоответствие единиц является частой причиной некорректного поведения функции.
Третий важный момент – анализ дискретизации. Частота дискретизации должна быть не менее двойной по отношению к частоте функции (условие Найквиста), чтобы избежать искажения формы и ошибки в расчетах, особенно при численном интегрировании и дифференцировании.
Рекомендуется использовать встроенные функции Mathcad для задания периода: например, переменные, явно задающие значение периода, что упрощает последующую проверку и изменение. Проверка осуществляется путем построения графика на интервале, превышающем период, и визуальной оценки совпадения начальной и конечной точек цикла.
Наконец, при сложных периодических функциях с несколькими частотами следует удостовериться в правильности каждого периода и учитывать их взаимодействие, иначе расчет приведет к неверной суперпозиции. Для этого можно выполнить разложение на гармоники и сопоставить период каждой составляющей.
Вопрос-ответ:
Как в Mathcad задать функцию с повторяющимся значением через определённый интервал?
Для задания функции, которая повторяется с фиксированным периодом, в Mathcad обычно используют оператор остатка от деления. Например, если функция f(t) задана на интервале от 0 до T, то для любого значения t периодическую функцию можно записать как f(t mod T). Такой подход позволяет вычислять значение функции в любой точке, повторяя исходный участок.
Можно ли задать периодическую функцию с разными видами повторяющихся участков в Mathcad?
Да, можно создать сложную периодическую функцию, комбинируя несколько различных фрагментов, каждый из которых определён на своём интервале периода. Для этого часто используют условные операторы, которые выбирают нужный кусок функции в зависимости от значения аргумента, приведённого к интервалу одного периода с помощью операции взятия по модулю.
Какие типичные ошибки возникают при определении периодической функции в Mathcad и как их избежать?
Одна из частых ошибок — неправильное использование оператора остатка, что приводит к неверному вычислению аргумента функции внутри периода. Также могут возникнуть сложности при смешивании скалярных и векторных значений в определениях. Для предотвращения таких проблем рекомендуется тщательно проверять выражения, использовать встроенные функции Mathcad для работы с модулем и тестировать функцию на разных значениях аргумента.
Как в Mathcad можно визуализировать периодическую функцию с несколькими периодами подряд?
Для построения графика функции на нескольких периодах достаточно задать диапазон аргумента, включающий несколько последовательных интервалов длины периода. Затем в графическом модуле Mathcad отображается функция в этом диапазоне, что наглядно демонстрирует её повторяемость. При необходимости можно использовать функции масштабирования и настройки осей для удобства просмотра.
Возможно ли задать периодическую функцию в Mathcad с изменяющимся периодом?
Стандартными средствами Mathcad реализовать функцию с меняющимся периодом сложно, так как периодическая функция по определению имеет постоянный период. Однако можно задать функцию с параметром, который влияет на длину периода, и вручную изменять этот параметр для разных вычислений. Для динамического изменения периода потребуется создавать отдельные выражения или скрипты, учитывающие вариации периода.