Для решения системы уравнений в Maple необходимо использовать встроенную команду LinearSolve или fsolve, в зависимости от типа уравнений. В случае линейных уравнений, достаточно представить их в виде матрицы коэффициентов и вектора правых частей. Для нелинейных уравнений предпочтительнее использовать fsolve, которая позволяет находить численные решения.
Пример задания линейной системы уравнений в Maple:
LinearSolve([[1, 2], [3, 4]], [5, 6]) – эта команда решит систему:
x + 2y = 5
3x + 4y = 6
Для решения нелинейной системы, состоящей из уравнений, например:
x^2 + y^2 = 1
xy = 0
используйте команду fsolve([x^2 + y^2 — 1, x*y], {x = 0, y = 0}).
При этом важно, чтобы начальные приближения (если это необходимо) были выбраны с учетом особенностей задач, например, для многократных корней или специфических областей. Maple эффективно справляется с различными типами систем, предлагая различные методы решения, включая аналитические и численные.
Подготовка переменных и уравнений для ввода
Для корректного ввода системы уравнений в Maple необходимо правильно подготовить переменные и выражения. Следует учитывать типы данных и синтаксис, принятые в этой системе. Рассмотрим основные шаги подготовки.
- Определение переменных: В Maple переменные автоматически считаются символическими, если они не были заданы как числовые. Для задания числовых значений используйте оператор
:=. Пример:x := 3. - Инициализация переменных: Если уравнение содержит параметры, то важно задать их заранее, чтобы избежать ошибок. Например, для задания переменной
aсо значением 5 используйте:a := 5. - Использование операторов: В Maple для обозначения стандартных математических операций (сложение, вычитание, умножение, деление) используются привычные операторы. Для умножения используйте знак
*, а для деления –/. - Система уравнений: Система уравнений вводится в виде списка уравнений, где каждое уравнение разделяется запятой. Уравнения разделяются знаком равенства (
=). Например, система уравнений:eq1 := x + y = 10, eq2 := 2*x - y = 5. - Использование точных значений: Для повышения точности решений рекомендуется использовать целые числа или дроби в виде
1/2, а не десятичные числа.
Подготовив переменные и уравнения, можно перейти к решению системы. Следует избегать лишних пробелов в синтаксисе и внимательно проверять корректность записи уравнений, чтобы не возникало ошибок в дальнейшем.
Использование команды `LinearSolve` для линейных систем
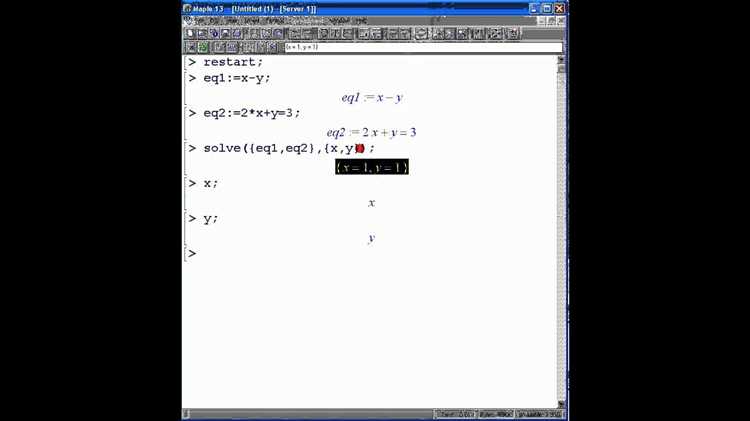
Команда `LinearSolve` в Maple предназначена для решения линейных систем уравнений. Для этого необходимо передать два аргумента: матрицу коэффициентов и вектор правых частей. Результатом работы команды будет вектор решений.
Пример использования: допустим, у нас есть система из двух уравнений с двумя неизвестными:
3x + 4y = 10 2x - y = 3
Для того чтобы решить её в Maple, нужно записать систему в виде матрицы и вектора:
A := Matrix([[3, 4], [2, -1]]); B := Vector([10, 3]);Теперь можно применить команду `LinearSolve`:
solutions := LinearSolve(A, B);После выполнения команды в переменной `solutions` будет храниться вектор с решениями системы. В данном примере, результатом будет вектор, содержащий значения переменных x и y.
Важно помнить, что команда `LinearSolve` работает только для системы линейных уравнений, где количество уравнений совпадает с количеством переменных. Если система несовместна или имеет бесконечно много решений, команда вернёт ошибку.
При использовании `LinearSolve` можно задать дополнительный параметр, указывающий на метод решения. По умолчанию Maple использует метод Гаусса, но для больших систем можно выбрать метод LU-разложения или другие алгоритмы, доступные в Maple. Например:
solutions := LinearSolve(A, B, method = "LU");Также стоит учитывать, что в случае вырожденных матриц (где определитель равен нулю), команда может вернуть ошибку или предупредить о невозможности найти решение.
Решение нелинейных систем уравнений с помощью Maple
Пример использования команды для решения системы:
> fsolve({x^2 + y^2 = 1, x + y = 1}, {x, y});Этот код решает систему из двух уравнений: окружность и прямая. Функция `fsolve` возвращает численные решения для переменных x и y.
Если необходимо получить все возможные решения системы, можно воспользоваться параметром `multiple`:
> fsolve({x^2 + y^2 = 1, x + y = 1}, {x, y}, multiple);Для более точных решений нелинейных уравнений рекомендуется использовать опцию `tolerance`, которая позволяет настроить точность решения:
> fsolve({x^2 + y^2 = 1, x + y = 1}, {x, y}, tolerance = 1e-6);Maple также поддерживает аналитическое решение через команду `solve`. Однако для сложных нелинейных систем предпочтительнее использовать численные методы, так как они обеспечивают более быстрые результаты:
> solve({x^2 + y^2 = 1, x + y = 1}, {x, y});В некоторых случаях можно применить метод Ньютона для численного решения. Для этого в Maple существует команда `Newton`:
> Newton({x^2 + y^2 = 1, x + y = 1}, {x, y});Кроме того, для оценки устойчивости решений и анализа поведения системы можно использовать визуализацию графиков с помощью команд `plot` или `contourplot`, что позволяет наглядно увидеть возможные пересечения кривых и области решений.
При решении нелинейных систем важно помнить, что численные методы могут не всегда давать точные результаты, особенно для сложных систем с множественными решениями или для систем, в которых решения расположены на границе области определения. Для повышения надежности решения необходимо правильно выбрать метод и задать соответствующие параметры погрешности.
Настройка параметров для численного решения уравнений
Для эффективного численного решения системы уравнений в Maple необходимо правильно настроить несколько ключевых параметров. Это поможет избежать ошибок вычислений и ускорить процесс нахождения решений.
Параметры метода решения: В Maple можно выбрать различные методы численного решения. Используйте параметр method, чтобы задать алгоритм. Например, метод Ньютона подходит для решений нелинейных уравнений, а метод Гаусса может быть полезен для линейных систем. Выбор метода зависит от типа уравнений и их сложности.
Точность решения: Параметр digits задает количество значащих цифр в ответе. Установка слишком высокой точности может привести к излишним вычислениям, замедляя процесс, в то время как низкая точность может привести к погрешностям. Оптимально использовать значение от 10 до 15 знаков.
Максимальное количество итераций: Параметр maxiter ограничивает количество итераций для численных методов. Для сложных задач увеличьте это значение, но помните, что слишком большое количество итераций может замедлить решение. Обычно достаточно 50-100 итераций для большинства задач.
Диапазон поиска решения: Укажите диапазон возможных значений переменных с помощью параметра range. Это ограничение важно для методов, чувствительных к начальным приближениями, таких как метод Ньютона. Установка слишком широкого диапазона может привести к неэффективным вычислениям, а слишком узкий – к пропуску решения.
Использование начальных приближений: В некоторых методах численного решения, таких как метод Ньютона или секущих, важно задать начальное приближение. Параметр initial guess помогает выбрать начальные значения для переменных. Убедитесь, что они близки к реальному решению, чтобы повысить эффективность алгоритма.
Решение с учетом погрешностей: В случае с многозначными решениями используйте параметр tolerance, чтобы задать допустимую погрешность. Этот параметр позволяет контролировать, насколько близко решение должно подходить к точному значению. Обычно значение от 1e-6 до 1e-9 является оптимальным.
Правильная настройка этих параметров в Maple обеспечит быстрое и точное решение системы уравнений. При этом важно учитывать тип задачи и особенности методов, чтобы минимизировать погрешности и время вычислений.
Как задать параметры и ограничения для системы уравнений
Пример задания параметров: если нужно задать параметр, например, переменную `a`, как положительное число, используйте следующий код:
assume(a > 0);Если переменная должна быть целым числом, применяется следующий синтаксис:
assume(a, integer);Для задания нескольких ограничений на переменную можно комбинировать условия, например, ограничить переменную как положительное целое число:
assume(a > 0, a, integer);Также возможно задать ограничения для нескольких переменных сразу. Например, чтобы объявить переменные `x` и `y` как вещественные числа, можно написать:
assume(x, y, real);Для ограничения системы уравнений на определённые диапазоны значений переменных можно использовать условные операторы. Например, для системы уравнений с ограничением на значения переменных в определённом диапазоне, можно задать:
assume(x > 1 and x < 10, y > 0 and y < 5);Если необходимо указать ограничения на функции или выражения, то можно использовать команды для сравнения, такие как `>=`, `<=`, и `<>`. Например, если нужно, чтобы функция `f(x)` всегда была больше нуля, можно использовать:
assume(f(x) > 0);Для работы с параметрами в Maple важно помнить, что установка ограничений влияет на точность и методы вычисления решений системы. Maple будет учитывать эти ограничения при вычислениях, что может повлиять на итоговое решение.
Чтобы вывести решение, необходимо использовать команду
solve, которая возвращает результат в виде структурированного объекта. Например:solve([x + y = 3, x - y = 1], [x, y]);Maple покажет решение в виде списка значений для переменных
xиy. В случае линейных систем, решение может быть представлено в виде числовых значений или символов, если система имеет параметрический характер. В случае нелинейных уравнений, решение может быть более сложным, например, в виде корней или рациональных выражений.Если система имеет бесконечное количество решений или не имеет решений, Maple предоставит соответствующие сообщения. Например, если система несовместна, будет выведено сообщение, указывающее на отсутствие решений. В случае, если система имеет бесконечное количество решений, Maple представит решение в виде параметрических выражений, где одна или несколько переменных будут выражены через параметры.
Для более глубокого анализа решения можно использовать команду
evalf, чтобы получить численные значения для корней системы, если это необходимо:evalf(solve([x^2 + y^2 = 1, x + y = 1], [x, y]));Если система решается поэтапно или имеет несколько решений, можно использовать команду
fsolveдля численного решения, что полезно при сложных нелинейных уравнениях. Эта команда позволяет задать начальные приближения для поиска решений.Решение следует интерпретировать в контексте задачи. Важно учитывать, что Maple может предложить несколько решений для одной и той же системы. Например, при решении системы дифференциальных уравнений могут быть представлены общие решения с произвольными постоянными, которые следует определить с помощью дополнительных условий.
Для анализа решения можно использовать команды для визуализации, такие как
plot, что поможет наглядно оценить поведение решения в различных точках пространства или во времени, если речь идет о динамических системах.Вопрос-ответ:
Как в Maple записать систему уравнений для решения?
В Maple система уравнений задаётся с помощью списка или множества, где каждое уравнение указывается отдельно. Например, для системы из двух уравнений нужно написать: {x + y = 5, x - y = 1}. Такое задание позволяет Maple понять, какие уравнения нужно решать совместно.
Можно ли использовать в системе уравнений в Maple несколько переменных и как это сделать?
Да, в Maple можно вводить уравнения с любым числом переменных. В списке уравнений просто указывайте уравнения, в которых участвуют нужные переменные, например: {x + y = 7, y - z = 3, x + z = 10}. Для решения при этом нужно явно перечислить все переменные, с которыми работаете, например, команда solve({…}, {x, y, z}).
Как задать систему нелинейных уравнений в Maple и получить решение?
Для задания нелинейных уравнений в Maple используют тот же способ, что и для линейных: список или множество уравнений. Например, {x^2 + y = 4, sin(x) + y = 1}. Для решения можно вызвать функцию solve, которая попытается найти все корни или подставить численные методы при необходимости, если точное решение недоступно.
Какие ошибки часто возникают при вводе системы уравнений в Maple и как их избежать?
Часто встречаются ошибки, связанные с синтаксисом: забытые фигурные скобки, неправильное использование знака равенства или отсутствие перечисления переменных при решении. Чтобы избежать проблем, убедитесь, что система заключена в фигурные скобки, уравнения написаны через знак «=», а функция solve получает список всех переменных, участвующих в системе.
Как вывести результаты решения системы уравнений в удобочитаемом виде в Maple?
Результат, который возвращает Maple после решения системы, обычно представлен в виде набора пар переменная = значение. Чтобы сделать вывод более понятным, можно использовать команды print или display. Также удобно преобразовать ответ в таблицу или присвоить значения переменным для дальнейшей работы с ними.
Как в Maple задать систему уравнений для решения?
В Maple систему уравнений можно задать с помощью оператора фигурных скобок, объединяя все уравнения в один набор. Например, чтобы записать систему из двух уравнений, нужно использовать синтаксис вида: {уравнение1, уравнение2}. После этого можно передать эту систему в функцию решения, например, `solve` или `fsolve`, в зависимости от задачи и типа уравнений. Такой подход позволяет работать с несколькими уравнениями одновременно.