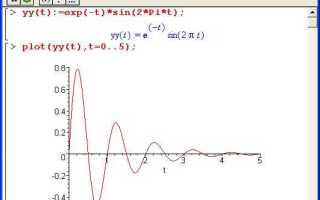
Символьная математика в Maple позволяет формализовать и решить систему уравнений с минимальными трудозатратами. Программная среда поддерживает ввод уравнений как в виде списка, так и с использованием функциональных конструкций вроде eq1 := lhs = rhs. При этом порядок задания переменных напрямую влияет на структуру и читаемость решений.
Для создания системы достаточно определить уравнения как выражения и объединить их в список или множество. Например, {x + y = 3, x — y = 1} – корректный способ задания системы из двух линейных уравнений. Чтобы Maple правильно интерпретировал входные данные, каждое уравнение должно быть записано с использованием оператора =, а не :=.
При работе с параметрическими системами рекомендуется использовать функцию solve с опцией parametric или применять solve совместно с assume для задания условий на параметры. Это особенно важно при моделировании физических процессов, где ограничения на параметры отражают реальные допущения задачи.
Как задать линейную систему уравнений с помощью списка
В Maple линейную систему удобно задавать в виде списка уравнений. Такой подход позволяет легко манипулировать системой, передавать её в функции и модифицировать.
Для задания системы выполните следующие шаги:
- Определите переменные с помощью команды
with(LinearAlgebra):илиwith(Student[LinearAlgebra]):при необходимости дальнейшей работы с матрицами. - Задайте уравнения в виде выражений. Например:
eq1 := 2*x + 3*y = 7:eq2 := -x + 4*y = 1:
- Объедините их в список:
system := [eq1, eq2]:
- Передайте список в функцию
solve:solve(system, [x, y]);
Если уравнения создаются программно, список формируется циклом или через генератор:
[seq(a[i]*x + b[i]*y = c[i], i = 1..n)].
Для хранения системы с возможностью повторного использования – присваивайте список переменной. Это упрощает передачу в LinearSolve, LUDecomposition и другие функции.
Использование массива уравнений для работы с нелинейными системами
Для задания нелинейной системы в Maple рекомендуется использовать массив или список уравнений, что обеспечивает удобную передачу системы в решающие процедуры, такие как solve или fsolve.
Создание массива уравнений осуществляется с помощью квадратных скобок. Например, система из двух уравнений:
eqs := [x^2 + y^2 = 1, x*y = 0.5];
Для решения системы символически применяют:
solve(eqs, [x, y]);
При работе с численным решением важно задать начальные приближения. Используется следующая конструкция:
fsolve(eqs, {x = 0.5, y = 0.5});
Если переменных больше двух, массив уравнений и массив переменных должны быть строго согласованы по структуре. Например, для трёх уравнений:
eqs := [x^2 + y^2 + z^2 = 3, x*y = 1, y*z = 1];
vars := [x, y, z];
solve(eqs, vars);
Для нелинейных систем, содержащих параметры, удобно использовать массив уравнений совместно с подстановкой значений параметров через subs:
subs(a=2, b=1, eqs);
Массив уравнений может быть динамически сформирован с помощью циклов или процедур. Это критично при моделировании с переменным числом уравнений. Например:
eqs := [seq(x[i]^2 — i = 0, i = 1..n)];
Для систем с несколькими решениями рекомендуется использовать опцию allsolutions:
solve(eqs, vars, allsolutions);
Функции eval и evalf позволяют получить приближённые значения решений или подставить найденные значения в другие выражения. Это особенно полезно после численного решения системы:
evalf(%);
Правильное использование массива уравнений обеспечивает масштабируемость и надёжность при работе с нелинейными моделями любой сложности.
Объявление переменных и управление порядком их подстановки
Пример объявления и использования переменных с контролем порядка:
restart;
eq1 := x + y - z = 0;
eq2 := 2*x - y + 3*z = 5;
eq3 := -x + 4*y + z = -2;
vars := [z, y, x];
solve({eq1, eq2, eq3}, vars);
Порядок переменных в списке vars определяет приоритет подстановки и упрощения. Maple разрешает неопределённости последовательно, начиная с первой переменной. Это критично при использовании solve, fsolve, isolve, где заданы многопеременные системы.
Для подстановки выражений используйте subs и управляйте очередностью явно:
sol := solve(eq1, z);
subs(sol, eq2); # сначала подставляется z
Чтобы задать переменные как символические объекты без текущих значений, применяйте assume или declare из пакета RealDomain, если требуется контекст реальности или ограничений:
assume(x, real);
assume(y > 0);
Также возможно управление упрощением через simplify и collect с указанием переменной, относительно которой производится группировка, что важно при подстановке и анализе выражений:
expr := subs(sol, eq3);
simplify(expr);
collect(expr, x);
Передача системы в функции solve, fsolve и LinearSolve
solve принимает систему в виде списка уравнений и соответствующий список переменных. Уравнения передаются как выражения с оператором = или как разности, приравненные к нулю. Пример:
solve({x + y = 5, x - y = 1}, {x, y});
Если список переменных не указан, Maple пытается выбрать их автоматически, что может привести к нежелательному порядку решений. Уточнение переменных критично при неоднозначности.
fsolve работает аналогично, но предназначен для численного решения. Требует указания начальных приближений или диапазонов для каждой переменной. Синтаксис:
fsolve({sin(x) = y, x + y = 2}, {x = 0..Pi, y});
Если диапазоны заданы только для части переменных, остальные ищутся на всём допустимом множестве, что может ухудшить точность. Рекомендуется задавать диапазоны для всех переменных.
LinearSolve используется только для линейных систем. Аргументы – матрица коэффициентов и вектор правых частей. Перед вызовом требуется привести систему к матричному виду с помощью GenerateMatrix:
A, b := GenerateMatrix({2*x + 3*y = 5, 4*x - y = 1}, {x, y});
LinearSolve(A, b);
Порядок переменных при генерации матрицы должен быть согласован с их позицией в векторе решений. LinearSolve возвращает только одно решение – при наличии параметров в общем решении они отбрасываются.
Для символьных линейных систем, где требуется общее решение, предпочтительнее solve. Для численного – fsolve в комбинации с LinearAlgebra[MatrixInverse] при необходимости.
Работа с параметрами и условными уравнениями в системе
В Maple параметры в системе уравнений задаются как обычные символы, не имеющие числового значения на момент определения системы. Это позволяет анализировать поведение решений в зависимости от значений параметров. Например, в системе уравнений:
eq1 := a*x + y = 3:
eq2 := x - b*y = 1:
символы a и b являются параметрами. Для получения решений с учётом параметров используется команда solve:
solve({eq1, eq2}, {x, y});
Если необходимо задать ограничения на параметры, используется синтаксис условий. Условное решение выполняется с помощью конструкции assuming:
solve({eq1, eq2}, {x, y}) assuming a <> 0, b > 0;
Для анализа случаев, когда параметры принимают критические значения (например, знаменатель обнуляется), применяется solve вместе с командой Cases или функцией piecewise. Пример разветвления в зависимости от параметра:
solve({a*x + y = 3, x + y = 2}, {x, y});
solve({a*x + y = 3, x + y = 2}, {x, y}) assuming a = 1;
Для проверки совместимости системы при разных значениях параметров полезна команда is:
is(a <> 1);
Для работы с параметрическими решениями, возвращающими выражения с произвольными параметрами, применяется опция parametric:
solve({x^2 + a*y = 1, y^2 + x = 2}, {x, y}, parametric);
Для генерации условий существования решения используется команда RealDomain:-solve с параметром allsolutions при необходимости:
RealDomain:-solve({x^2 + a*x + 1 = 0}, x, allsolutions);
При анализе систем с условиями часто применяется select в сочетании с eval для фильтрации решений по параметрическим ограничениям:
select(u -> eval(u, a=2) <> FAIL, sol);
Условные уравнения удобно задаются через piecewise, позволяя построить системы с разными ветвями в зависимости от параметров:
eq := piecewise(a > 0, x + y = 1, a <= 0, x - y = 1);
Такой подход позволяет точно контролировать логику изменения системы при варьировании параметров и получать корректные аналитические выражения.
Преобразование системы уравнений в матричную форму

В Maple для работы с линейными системами удобно использовать матричное представление Ax = b. Для преобразования заданной системы уравнений необходимо выделить коэффициенты при переменных и свободные члены.
Основной инструмент – функция LinearAlgebra[Matrix], которая создаёт матрицу из списка коэффициентов. Коэффициенты извлекаются с помощью coeff, а переменные фиксируются в конкретном порядке, что критично для правильного формирования матрицы.
Пример: при системе уравнений вида 3x + 2y = 5, 4x — y = 1 нужно задать список переменных vars := [x, y], а затем собрать матрицу коэффициентов A := Matrix([[coeff(lhs(eq1), x), coeff(lhs(eq1), y)], [coeff(lhs(eq2), x), coeff(lhs(eq2), y)]]).
Свободные члены формируются через вектор b := Vector([rhs(eq1), rhs(eq2)]). Такой подход гарантирует правильное расположение элементов в матрице и векторе, что критично для последующего решения и анализа.
Если система задана в общем виде или численно, используйте map и seq для автоматизации извлечения коэффициентов, избегая ручного ввода. Например, A := Matrix([seq([seq(coeff(lhs(eq), var) for var in vars)], eq in eqs)]), где eqs – список уравнений.
После формирования матрицы и вектора следует проверить размерность и корректность данных с помощью LinearAlgebra[Dimension] и визуализации MatrixPlot для быстрого выявления ошибок.
Вопрос-ответ:
Как в Maple правильно задать систему уравнений с несколькими переменными?
Для задания системы уравнений в Maple необходимо использовать фигурные скобки и знак равенства для каждого уравнения. Переменные указываются после двоеточия или через запятую. Например, система из двух уравнений записывается так: system := {x + y = 5, x — y = 1};. Затем её можно решать с помощью команды solve(system, {x, y});, где {x, y} — переменные, которые нужно найти.
Можно ли в Maple задавать системы уравнений с параметрами и как тогда происходит решение?
Да, в Maple допускается задавать системы с параметрами. В уравнениях можно оставлять неизвестные коэффициенты или параметры, например a, b и т.д. При решении команда solve попытается выразить переменные через эти параметры. Если система решается, результат будет содержать параметры как символы, что позволяет исследовать зависимости решений от их значений. Такой подход удобен для анализа различных вариантов задачи.
Какие типичные ошибки возникают при вводе системы уравнений в Maple, и как их избежать?
Основные ошибки связаны с синтаксисом: пропуск фигурных скобок, неправильное использование знака равенства (например, знак присваивания := вместо =), либо отсутствие запятых между уравнениями. Еще часто встречается ситуация, когда переменные не указаны явно при вызове solve, что может привести к частичным или неверным результатам. Чтобы избежать таких ошибок, стоит внимательно проверять структуру записи и использовать подсказки среды Maple.
Как можно задать нелинейную систему уравнений в Maple и получить ее численное решение?
Для нелинейных систем уравнений в Maple можно задать их аналогично линейным, но при решении использовать функцию fsolve, которая ищет численные корни. Например: system := {x^2 + y^2 = 4, x*y = 1}; fsolve(system, {x, y}); — так Maple попытается найти численные значения переменных, удовлетворяющие системе. Такой способ подходит, когда аналитическое решение сложно или невозможно получить.