Функция арктангенса (atan) в Mathcad реализована стандартно, но её ввод часто вызывает вопросы из-за особенностей синтаксиса и диапазона значений. Для корректного отображения результата важно использовать правильный формат записи, который учитывает входные данные и назначение вычислений.
Основной способ ввода арктангенса в Mathcad – использование функции atan(x), где x – числовое выражение или переменная. Этот метод обеспечивает вычисление угла в радианах, соответствующего значению тангенса.
Если требуется работать с углами в градусах, после вызова atan необходимо применить преобразование результата с помощью функции deg(). Например, deg(atan(x)) даст значение угла в градусах, что упрощает интерпретацию и использование результатов в инженерных расчетах.
Для обработки комплексных значений или расширения области определения применяется функция atan2(y, x), которая возвращает угол по координатам. В Mathcad эта функция часто записывается как atan2(y, x) и позволяет корректно вычислять угол в четырех квадрантах, избегая неоднозначностей.
Формат ввода функции арктангенса в Mathcad
В Mathcad для вычисления арктангенса используется стандартная функция atan(x), где x – аргумент функции. Ввод осуществляется через клавиатуру, без пробелов между именем функции и скобками.
Аргумент x может быть числом, переменной или выражением, например: atan(0.5), atan(a/b). Результат возвращается в радианах, что важно учитывать при последующих расчетах и преобразованиях углов.
Для удобства работы с углами в градусах рекомендуется применять преобразование результата: atan(x) * 180/π, где π – встроенная константа Mathcad (pi или π).
Если необходимо вычислить арктангенс с двумя аргументами для учета знаков координат (аналог функции atan2(y, x) в других системах), в Mathcad следует использовать комбинацию условий или вручную проверять знаки, так как встроенного оператора atan2 нет.
При работе с векторами или массивами Mathcad автоматически применяет функцию atan поэлементно, что упрощает обработку данных без необходимости циклов или дополнительных команд.
Использование встроенной функции atan для вычисления арктангенса
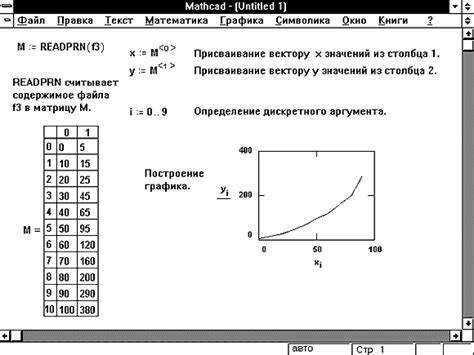
В Mathcad вычисление арктангенса реализуется с помощью встроенной функции atan. Она принимает один числовой аргумент – значение тангенса угла – и возвращает угол в радианах в диапазоне от -π/2 до π/2.
Для вызова функции достаточно ввести atan(x), где x – число или выражение. Результат пригоден для дальнейших математических операций, преобразований и визуализации.
Если требуется результат в градусах, следует умножить возвращаемое значение на 180/π или применить встроенную функцию преобразования углов.
Для корректного вычисления арктангенса с учетом знаков обеих координат, например, при работе с декартовыми координатами, рекомендуется использовать функцию atan2(y, x). Она возвращает угол, расположенный в правильном квадранте.
Использование atan обеспечивает простоту и точность вычислений без необходимости писать сложные формулы или применять дополнительные преобразования.
Обработка аргументов с учётом квадранта через atan2

Функция atan2(y, x) в Mathcad обеспечивает вычисление арктангенса с учётом знаков обеих координат, что позволяет определить угол в правильном квадранте. В отличие от обычного atan(y/x), где необходимо дополнительно анализировать знаки, atan2 возвращает результат в диапазоне от –π до π, автоматически учитывая положение в системе координат.
Для корректного использования atan2 в Mathcad важно подавать аргументы в формате atan2(ordinate, abscissa), то есть y и x. Это гарантирует точный угол в радианах без дополнительной обработки. При работе с градусами рекомендуется применять преобразование через умножение результата на 180/π.
Если функция недоступна в стандартном наборе Mathcad, её можно реализовать вручную через проверку знаков и вызовы atan, используя следующий алгоритм:
– если x > 0, результат равен atan(y/x);
– если x < 0 и y ≥ 0, результат равен atan(y/x) + π;
– если x < 0 и y < 0, результат равен atan(y/x) — π;
– если x = 0 и y ≠ 0, угол равен ±π/2 в зависимости от знака y.
Такой подход позволяет полноценно воспроизвести поведение atan2 и точно определять угол в нужном квадранте без ошибок, возникающих при делении на ноль или игнорировании знаков.
Запись арктангенса с ограничениями на область определения

В Mathcad функция арктангенса (atan) имеет область определения по всему множеству вещественных чисел. Однако в практических задачах важно учитывать ограничения, связанные с конкретной областью значений аргумента.
Для корректного задания арктангенса с ограничениями на область определения в Mathcad следует использовать проверку аргумента перед вызовом функции. Это можно реализовать с помощью условных операторов:
- Определить допустимый диапазон аргумента, например,
x_minиx_max. - Использовать конструкцию
ifдля проверки, попадает ли значение в этот диапазон. - При выходе за пределы диапазона возвращать сообщение об ошибке или значение по умолчанию.
Пример записи:
if(x >= x_min and x <= x_max, atan(x), "Ошибка: x вне области определения")Если необходимо ограничить результат арктангенса, например, чтобы значение угла не выходило за определённый интервал, рекомендуется дополнительно использовать функции min и max:
angle := atan(x)
angle_limited := max(min(angle, angle_max), angle_min)- Такой подход гарантирует, что результат функции останется в нужных пределах.
- При работе с комплексными аргументами нужно дополнительно учитывать область определения комплексного арктангенса.
Важный момент: Mathcad не имеет встроенной функции с явным ограничением области определения арктангенса, поэтому все проверки необходимо выполнять вручную с помощью логических операторов.
Практические примеры вычисления арктангенса в Mathcad

Для вычисления арктангенса в Mathcad достаточно использовать встроенную функцию atan. Рассмотрим несколько практических случаев с разбором особенностей записи и интерпретации результата.
- Вычисление арктангенса числа:
Введите выражение
atan(1), Mathcad вернёт значение π/4 (примерно 0.7854). Результат по умолчанию в радианах. - Переход к градусам:
Для получения результата в градусах умножьте значение на
180/πили используйте функциюdeg(atan(x)). - Арктангенс для отрицательных и больших значений:
Функция
atanкорректно вычисляет значение для отрицательных аргументов, например,atan(-1)даст -π/4. Для значений больше единицы, например,atan(10), возвращается угол, близкий к π/2, что соответствует теории. - Использование atan2 для координат:
Для вычисления угла точки с координатами (y, x) относительно оси абсцисс применяйте функцию
atan2(y, x). Например,atan2(1, -1)выдаст угол около 135° (в радианах ≈ 2.356), учитывая правильный квадрант. - Практический пример: определение угла наклона линии:
- Задайте координаты двух точек:
(x1, y1)и(x2, y2). - Вычислите угловой коэффициент:
k := (y2 - y1) / (x2 - x1). - Найдите угол наклона:
α := atan(k). - При необходимости переведите угол в градусы:
deg(α).
- Задайте координаты двух точек:
- Рекомендации:
- Убедитесь, что единицы углов корректно заданы (радианы или градусы) для дальнейших вычислений.
- При работе с комплексными числами функция
atanвозвращает комплексный результат, что требует дополнительной интерпретации. - Для повышения читаемости формул используйте переменные вместо длинных выражений внутри функций.
Автоматизация вычислений арктангенса с помощью пользовательских функций
В Mathcad создание пользовательских функций для вычисления арктангенса позволяет стандартизировать и ускорить работу с угловыми величинами. Для определения функции используйте синтаксис:
atan_func(x) := arctan(x)
где atan_func – имя функции, а x – входной параметр.
Для обработки массивов значений параметр x может быть вектором или матрицей, что позволяет автоматически применять функцию ко всем элементам без дополнительного цикла.
Рекомендуется дополнительно включить проверку диапазона входных данных для предотвращения ошибок при неверных аргументах. Например, с помощью условных операторов можно вернуть сообщение об ошибке или скорректировать значение:
atan_safe(x) := if |x| ≤ 10 then arctan(x) else "Ошибка: аргумент вне диапазона"
Для удобства работы с градусной мерой можно расширить функцию, переводя результат из радиан в градусы:
atan_deg(x) := (180/π) * arctan(x)
Хранение таких функций в библиотеке Mathcad обеспечивает быстрый доступ и повторное использование в различных проектах, что значительно экономит время при решении инженерных задач.
Вопрос-ответ:
Как в Mathcad записать арктангенс с использованием стандартных функций?
В Mathcad арктангенс можно записать с помощью функции atan(x), где x — аргумент. Она вычисляет угол в радианах, чей тангенс равен заданному числу. Такая запись считается базовой и подходит для большинства вычислений, связанных с обратным тангенсом.
Можно ли в Mathcad получить арктангенс сразу в градусах, не переводя результат вручную?
Да, в Mathcad можно сразу получить результат в градусах, если использовать встроенную функцию преобразования углов или задать единицу измерения результата как градусы. Например, после вычисления atan(x) нужно умножить результат на 180/π либо установить в настройках документа вывод углов в градусах, что упростит работу и избавит от необходимости конвертации.
Существуют ли альтернативные способы записи арктангенса в Mathcad, если функция atan недоступна?
Если по каким-то причинам функция atan недоступна, можно использовать выражение arctan(x) через встроенный оператор invtan или формулы, основанные на логарифмах комплексных чисел. Однако такие способы менее удобны и применяются редко. Наиболее простой вариант — проверить наличие стандартной функции и использовать ее напрямую.
Как избежать ошибок при вводе аргумента функции арктангенс в Mathcad?
Чтобы избежать ошибок, важно вводить аргумент в допустимом числовом формате и следить за областью определения функции. Арктангенс определен для всех действительных чисел, но если используется комплексный аргумент, нужно убедиться, что Mathcad корректно распознает тип данных. Также полезно проверять синтаксис выражения и правильно использовать скобки.
Можно ли упростить запись арктангенса в Mathcad для часто повторяющихся вычислений?
Да, можно создать собственную функцию или переменную, которая будет содержать выражение для арктангенса, и использовать её в расчетах. Это позволяет избежать многократного ввода однотипных выражений и ускоряет работу. Например, задайте f(x):=atan(x), после чего вызывайте f для любых значений x.