Как посчитать дисперсию в python

Дисперсия – это мера разброса значений в наборе данных. В Python для её вычисления достаточно использовать базовые средства языка или сторонние библиотеки. В этой статье мы пошагово рассмотрим, как вычислить дисперсию вручную и с использованием популярных библиотек, таких как NumPy.

Для начала определим, что такое дисперсия. Это среднее арифметическое квадрата отклонений каждого значения от средней величины выборки. В Python существует несколько способов её вычисления: от ручного подсчета до использования готовых функций. Мы сосредоточимся на простоте и точности, начиная с теоретической основы и заканчивая практическими примерами.

Важное замечание: дисперсия может быть рассчитана как для всего набора данных (всей популяции), так и для выборки, что важно учитывать при применении формул. В случае выборки важно использовать формулу, которая учитывает степень свободы, чтобы результат был более точным.

Теперь рассмотрим, как это сделать в Python, начиная с ручного подсчета и постепенно переходя к использованию библиотеки NumPy, которая упрощает работу с математическими вычислениями и большими массивами данных.

Подготовка данных для расчета дисперсии

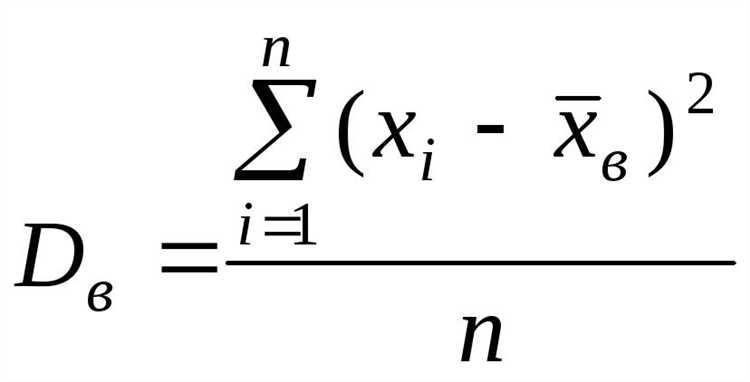
Перед вычислением дисперсии важно правильно подготовить данные. Для этого необходимо удостовериться, что набор данных не содержит ошибок и аномальных значений, которые могут исказить результаты. В первую очередь стоит проверить следующие моменты:

1. Отсутствие пропусков. Если в данных присутствуют пропущенные значения, их следует обработать. Один из вариантов – заменить пропуски средним значением по колонке или медианой. Для числовых данных можно использовать `pandas.fillna()`.

2. Нормальность распределения. Хотя дисперсия сама по себе не зависит от формы распределения, для интерпретации результата полезно понимать, насколько данные близки к нормальному распределению. Это можно проверить с помощью теста Шапиро-Уилка или графиков, таких как гистограммы и Q-Q графики.

3. Удаление выбросов. Выбросы могут существенно повлиять на результаты расчета дисперсии. Для их идентификации можно использовать методы, такие как межквартильный размах (IQR) или стандартное отклонение. Выбросы следует либо удалить, либо заменить на более подходящие значения.

4. Тип данных. Все данные, которые используются для вычисления дисперсии, должны быть числовыми. В случае категориальных данных их необходимо преобразовать в числовой формат, например, с помощью кодирования категорий.

После выполнения этих шагов можно приступать к расчету дисперсии. Важно помнить, что дисперсия вычисляется для числовых данных, а подготовка данных влияет на точность и интерпретируемость конечного результата.

Как использовать стандартные библиотеки Python для вычислений

Для выполнения математических расчетов в Python достаточно использовать стандартные библиотеки, такие как math и statistics, которые включают все необходимые функции для работы с числовыми данными.

Модуль math предоставляет инструменты для выполнения базовых математических операций. Например, функции для вычисления квадратного корня math.sqrt() или экспоненты math.exp(). Однако для статистических вычислений, таких как вычисление дисперсии или стандартного отклонения, лучше использовать модуль statistics.

Модуль statistics предлагает функцию variance(), которая позволяет вычислить дисперсию набора данных. Пример использования:

import statistics
data = [1, 2, 3, 4, 5]
variance = statistics.variance(data)
print(variance)

Эта функция автоматически обрабатывает данные, вычисляя дисперсию для выборки. Если нужно вычислить дисперсию для всей совокупности данных, используйте statistics.pvariance().

Кроме того, для комплексных вычислений можно использовать numpy (хотя это уже не стандартная библиотека, а сторонняя). Она предоставляет более высокую производительность при работе с большими массивами данных. Однако для большинства задач, связанных с дисперсией, встроенных возможностей Python будет достаточно.

Как вычислить дисперсию вручную с помощью формулы

Дисперсия (σ²) = (1 / N) * Σ(xᵢ — μ)²

где:

• σ² – дисперсия;
• μ – среднее значение набора данных;
• xᵢ – отдельные значения в наборе данных;
• N – общее количество значений в наборе;
• Σ – знак суммы, который указывает, что нужно суммировать значения, полученные после вычитания среднего из каждого элемента.

Шаги для вычисления дисперсии:

1. Найдите среднее значение (μ). Для этого сложите все значения в наборе данных и разделите на их количество. Формула: μ = Σxᵢ / N.
2. Вычислите отклонения каждого значения от среднего. Для этого вычитайте среднее значение (μ) из каждого элемента набора данных (xᵢ). Формула: xᵢ — μ.
3. Возведите отклонения в квадрат. Это нужно для устранения отрицательных значений и усиления влияния больших отклонений. Формула: (xᵢ — μ)².
4. Найдите сумму квадратов отклонений. Просуммируйте все квадраты отклонений, полученные на предыдущем шаге. Формула: Σ(xᵢ — μ)².
5. Разделите сумму квадратов отклонений на количество значений (N). Это и будет дисперсией. Формула: σ² = Σ(xᵢ — μ)² / N.

Например, если у вас есть данные 5, 7, 9, 10, то:

• Среднее значение (μ) = (5 + 7 + 9 + 10) / 4 = 7.75
• Отклонения от среднего: 5 — 7.75 = -2.75, 7 — 7.75 = -0.75, 9 — 7.75 = 1.25, 10 — 7.75 = 2.25
• Квадраты отклонений: (-2.75)² = 7.5625, (-0.75)² = 0.5625, (1.25)² = 1.5625, (2.25)² = 5.0625
• Сумма квадратов отклонений: 7.5625 + 0.5625 + 1.5625 + 5.0625 = 14.75
• Дисперсия: 14.75 / 4 = 3.6875

Таким образом, дисперсия этого набора данных равна 3.6875.

Отличие дисперсии выборки от дисперсии генеральной совокупности

Дисперсия генеральной совокупности вычисляется по формуле:

σ² = (Σ(xᵢ - μ)²) / N

где:

• σ² – дисперсия генеральной совокупности,
• xᵢ – отдельные значения данных,
• μ – математическое ожидание (среднее) генеральной совокупности,
• N – количество элементов в совокупности.

Дисперсия генеральной совокупности делится на квадрат разности между каждым элементом и средним значением всех данных, после чего результат суммируется и делится на общее количество элементов. Это дает точное измерение вариативности, если мы имеем доступ ко всей совокупности.

Дисперсия выборки в отличие от этого рассчитывается по формуле:

s² = (Σ(xᵢ - x̄)²) / (n - 1)

где:

• s² – дисперсия выборки,
• xᵢ – отдельные значения выборки,
• x̄ – выборочное среднее,
• n – количество элементов в выборке.

Для выборки используется деление на (n — 1), а не на n, как в случае с генеральной совокупностью. Этот коэффициент называется корректирующим коэффициентом Бесселя. Его цель – компенсировать систематическую ошибку, которая возникает из-за того, что выборка обычно дает недооценку дисперсии генеральной совокупности. Использование (n — 1) обеспечивает более точную оценку дисперсии генеральной совокупности, если выборка мала.

Важно помнить, что выборка, в отличие от генеральной совокупности, представляет собой лишь часть всей популяции, и ее дисперсия часто является лишь приблизительным значением для дисперсии всей совокупности. Именно поэтому формула для дисперсии выборки учитывает это уменьшение точности.

Если объем выборки достаточно велик, разница между дисперсией выборки и дисперсией генеральной совокупности минимальна. Однако для маленьких выборок корректировка становится важным элементом в расчетах.

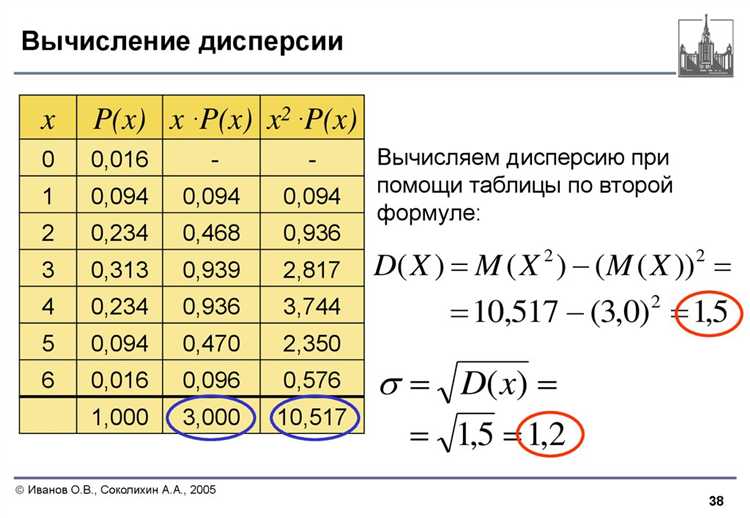
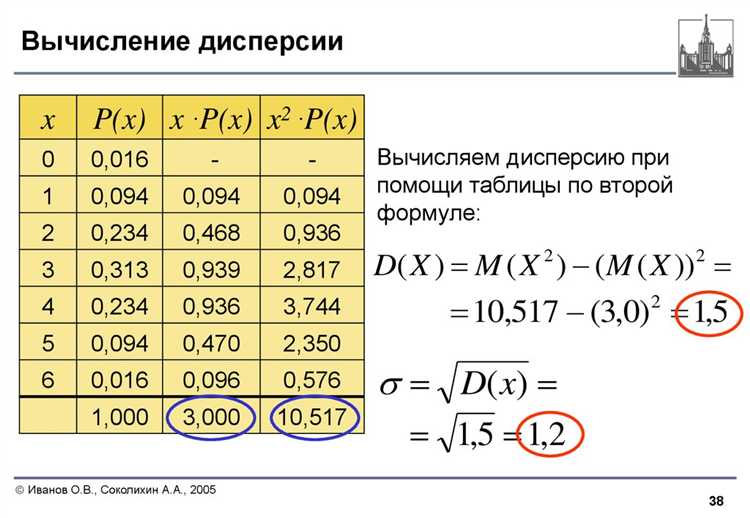
Использование библиотеки NumPy для вычисления дисперсии

Библиотека NumPy в Python предоставляет удобные средства для работы с массивами и выполнения статистических расчетов, включая вычисление дисперсии. Для этого используется функция numpy.var(), которая вычисляет дисперсию выборки или всей генеральной совокупности.

Основная формула для дисперсии выглядит так:

D = 1/n * Σ(xi - x̄)²

где xi – это отдельные элементы выборки, x̄ – среднее значение, n – количество элементов.

Для начала необходимо установить и импортировать библиотеку NumPy:

import numpy as np

Пример вычисления дисперсии:

data = np.array([1, 2, 3, 4, 5])
dispersion = np.var(data)
print(dispersion)

По умолчанию numpy.var() вычисляет дисперсию для всей выборки, предполагая, что данные представляют собой генеральную совокупность. Для вычисления дисперсии выборки с поправкой на степень свободы необходимо использовать параметр ddof (degrees of freedom). Для стандартной выборки ddof=1:

sample_dispersion = np.var(data, ddof=1)
print(sample_dispersion)

При необходимости можно вычислить дисперсию по каждой оси многомерного массива:

data_2d = np.array([[1, 2, 3], [4, 5, 6]])
dispersion_axis_0 = np.var(data_2d, axis=0)
dispersion_axis_1 = np.var(data_2d, axis=1)
print(dispersion_axis_0)
print(dispersion_axis_1)

Важное замечание: функция numpy.var() возвращает значение дисперсии, которое зависит от количества элементов и от выбранного параметра ddof. Если ddof=0, это будет дисперсия для генеральной совокупности, если ddof=1, то для выборки.

Использование NumPy для вычисления дисперсии позволяет легко обрабатывать как одномерные, так и многомерные массивы данных, что делает библиотеку удобной для анализа больших объемов информации в научных и инженерных расчетах.

Как проверить правильность расчета дисперсии в Python

Для начала следует рассчитать дисперсию вручную по формуле. Если используется выборочная дисперсия, формула такая: сумма квадратов отклонений от среднего, делённая на (n — 1), где n – количество элементов.

Пример данных: data = [2, 4, 4, 4, 5, 5, 7, 9]. Среднее: mean = sum(data) / len(data), то есть 5.0. Сумма квадратов отклонений: sum((x - mean) ** 2 for x in data) даст 32. Делим на 7 (n — 1): результат – 4.57 (приблизительно).

Для сравнения можно использовать statistics.variance(data) – стандартная функция Python для выборочной дисперсии. Ожидаемое значение должно совпасть с ручным расчётом. Для проверки общей (несмещённой) дисперсии используйте statistics.pvariance(data).

Дополнительно можно сверить результат с функцией numpy.var(data, ddof=1). Параметр ddof=1 задаёт расчёт по формуле выборочной дисперсии. Если результат отличается, проверьте исходные данные и точность округления.

Ещё один способ – протестировать функцию на искусственно заданных массивах с известной дисперсией, например, [0, 0, 0, 10, 10, 10]. Среднее – 5.0, дисперсия – 25. Используйте её как эталон для проверки кода.

Применение дисперсии для анализа данных в Python

Дисперсия – ключевой показатель разброса значений. В Python её активно используют для оценки стабильности, однородности и выявления аномалий в данных.

• В задачах машинного обучения с помощью дисперсии анализируют признаки: низкая дисперсия может указывать на отсутствие информативности, такие признаки часто исключают перед обучением моделей.
• В статистике и исследовательском анализе с её помощью сравнивают группы: если дисперсии сильно различаются, это влияет на выбор методов (например, при проведении t-теста).
• В проверке качества данных дисперсия помогает выявить колонки с константными или почти константными значениями – такие признаки искажают модель.

Рекомендуется использовать:

1. numpy.var() – для числовых массивов; указывайте ddof=1 для несмещённой оценки.
2. pandas.DataFrame.var() – для анализа всех столбцов сразу; удобно при работе с датафреймами.
3. sklearn.feature_selection.VarianceThreshold – для автоматического исключения признаков с низкой дисперсией (по умолчанию – нулевая).

Пример фильтрации признаков с низкой дисперсией:

from sklearn.feature_selection import VarianceThreshold
selector = VarianceThreshold(threshold=0.01)
X_reduced = selector.fit_transform(X)

Перед применением важно нормализовать данные, если признаки имеют разные масштабы. В противном случае дисперсия может вводить в заблуждение.

Вопрос-ответ:

Что такое дисперсия и зачем её считать в Python?

Дисперсия — это числовой показатель, отражающий степень разброса значений относительно их среднего. Она помогает понять, насколько данные стабильны или изменчивы. В Python её вычисляют, например, при анализе результатов экспериментов, финансовых показателей, пользовательской активности и других данных, где важно учитывать колебания. Работа с дисперсией особенно полезна в статистике, машинном обучении и аналитике.

Чем отличается дисперсия с параметром ddof=1 от дисперсии по умолчанию?

Параметр `ddof` в функциях `numpy.var()` и `pandas.Series.var()` указывает на степень смещения оценки дисперсии. По умолчанию `ddof=0`, что даёт смещённую оценку (используется при работе с генеральной совокупностью). Если установить `ddof=1`, то получится несмещённая оценка дисперсии, более подходящая для выборки. Например, `numpy.var(data, ddof=1)` — стандартный способ посчитать дисперсию выборки, аналогичный формуле с делением на \( n — 1 \).