Как посчитать логарифм в python

Модуль math в Python предоставляет функции log(), log10() и log2() для вычисления логарифмов с произвольным, десятичным и двоичным основанием соответственно. Все функции принимают числа с плавающей запятой и возвращают результат в формате float.

Функция math.log(x, base) используется, если требуется указать нестандартное основание. Например, math.log(100, 5) вернёт логарифм числа 100 по основанию 5, то есть приблизительно 2.861. Если второй аргумент опущен, функция вычисляет натуральный логарифм по основанию e.

math.log10(x) и math.log2(x) оптимизированы под частные случаи и работают быстрее, чем log() с соответствующим основанием. Например, math.log10(1000) вернёт 3.0, а math.log2(8) – 3.0. Использование этих функций предпочтительнее, если известно точное основание.

В случае работы с массивами чисел удобнее использовать NumPy. Функции numpy.log(), numpy.log10() и numpy.log2() применяются ко всем элементам массива. Это позволяет избежать циклов и сократить код. Например, numpy.log2(numpy.array([2, 4, 8])) вернёт массив [1., 2., 3.].

Перед вычислением логарифма следует проверить, что аргумент больше нуля. Попытка передать ноль или отрицательное значение вызовет исключение ValueError. Для безопасной обработки входных данных можно использовать проверку через if x > 0 или обработку исключений с try/except.

Как вычислить натуральный логарифм с помощью math.log()

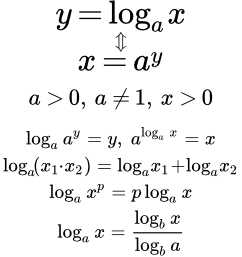
Функция math.log() из стандартного модуля math позволяет вычислять натуральный логарифм (по основанию e) числа. Формат вызова:

import math
результат = math.log(x)

Где x – положительное число. При передаче значения меньше или равного нулю возникнет ошибка ValueError.

Примеры:

import math
print(math.log(1))        # 0.0
print(math.log(math.e))   # 1.0
print(math.log(10))       # ≈ 2.302585092994046

Если нужно рассчитать логарифм по другому основанию, можно указать второй аргумент:

math.log(100, 10)  # логарифм 100 по основанию 10, результат: 2.0

Для получения только натурального логарифма используйте вызов с одним аргументом. Функция math.log() возвращает число типа float, результат точен до 15–17 значащих цифр.

При работе с массивами чисел предпочтительнее использовать numpy.log() для векторизации вычислений.

Вычисление логарифма по основанию 10 через math.log10()

Функция math.log10(x) из стандартного модуля math возвращает десятичный логарифм числа x. Значение x должно быть положительным, иначе будет вызвано исключение ValueError.

Пример использования:

import math
результат = math.log10(1000)
print(результат)  # 3.0, так как 103 = 1000

значение = round(math.log10(5000), 4)
print(значение)  # 3.6989

import math
массив = [10, 100, 1000]
логарифмы = [math.log10(x) for x in массив]
print(логарифмы)  # [1.0, 2.0, 3.0]

import math
результат = math.log(81, 3)
print(результат)  # 4.0

math.log(10)  # Эквивалентно math.log(10, math.e)

math.log(x) / math.log(b)

Если требуется обработка вектора или матрицы, math будет выдавать ошибку TypeError. numpy позволяет обрабатывать списки и массивы без явной итерации. Например, numpy.log([1, e, e2]) вернёт [0., 1., 2.].

По скорости numpy выигрывает на больших объёмах данных благодаря векторизации. Для единичных вычислений разницы почти нет.

Для скаляров и указания произвольного основания – math. Для массивов и массовой обработки – numpy.

Обработка ошибок при вычислении логарифма отрицательных чисел

В стандартной библиотеке Python функция math.log() вызывает исключение ValueError, если переданное значение меньше или равно нулю. Например, math.log(-5) приведёт к ошибке: ValueError: math domain error. Это поведение соответствует математическим ограничениям логарифмической функции в действительной области.

Для проверки аргумента до вызова math.log() рекомендуется использовать условие: if x > 0. Это предотвращает выполнение недопустимых операций и избавляет от необходимости обрабатывать исключение.

Если требуется логарифм отрицательных чисел в комплексной области, следует использовать модуль cmath. Вызов cmath.log(-5) вернёт результат (1.6094379124341003+3.141592653589793j), что соответствует натуральному логарифму по комплексной формуле: ln|x| + i·arg(x).

Для перехвата ошибок при работе с реальными числами можно использовать конструкцию try...except:

import math
x = -5
try:
result = math.log(x)
except ValueError:
result = None

Это позволяет задать поведение при недопустимом входе, например, вывести предупреждение, записать лог или пропустить значение.

Нельзя использовать math.log() без предварительной проверки, если данные получены извне или вычислены динамически. Для массовой обработки чисел безопаснее фильтровать данные перед применением логарифмической функции:

import math
data = [-2, 0.5, 3, -1, 10]
logs = [math.log(x) for x in data if x > 0]

Если отрицательные значения допустимы в контексте задачи, но требуется использовать их логарифмы, необходимо явно перейти к комплексной арифметике с cmath.log(), сохраняя осознанность последствий.

Как применять логарифм в задачах масштабирования и нормализации данных

Логарифм часто используется для преобразования данных в задачи масштабирования и нормализации, когда необходимо снизить влияние выбросов или уменьшить разброс значений в наборах данных. Применение логарифмирования помогает преобразовать данные, распределённые по экспоненциальному закону, в более стабильную и симметричную форму, что улучшает качество моделей машинного обучения.

Один из основных случаев использования логарифмов – это уменьшение сильного скоса в распределении данных. Например, если в данных присутствуют значения с большой амплитудой, использование логарифма позволяет уменьшить разницу между максимальными и минимальными значениями. Это особенно важно для алгоритмов, чувствительных к масштабу, таких как методы кластеризации или линейные модели.

Для применения логарифмирования часто используют формулы вида: log(x + 1), чтобы избежать математических ошибок, когда входные данные содержат нули или отрицательные значения. Логарифмирование с добавлением единицы помогает работать с такими данными, не изменяя их структуры.

Пример использования логарифма в Python для нормализации данных:

import numpy as np
data = [1, 10, 100, 1000, 10000]
log_data = np.log1p(data)  # log(x + 1) для обработки нулевых значений
print(log_data)

В данном примере значения, находящиеся на различных порядках величины, приводятся к более схожей шкале, что позволяет алгоритмам машинного обучения работать с ними эффективнее.

Другим вариантом является использование логарифма с основанием 10 для приведения данных к шкале, где каждый шаг соответствует увеличению на порядок. Это может быть полезно, если важно сохранить пропорциональные отношения между значениями, но уменьшить их абсолютные различия.

Логарифмирование также помогает улучшить эффективность обработки данных в задачах, связанных с прогнозированием временных рядов или с экономическими моделями, где изменения могут быть экспоненциальными. В таких случаях логарифмирование позволяет значительно уменьшить влияние резких колебаний данных, делая их более пригодными для предсказаний.

Вопрос-ответ: