Для анализа данных и моделирования их распределений Python предлагает мощные инструменты, которые позволяют строить точные графики и проводить глубокую статистическую обработку. Построение распределений помогает визуализировать, как значения данных распределены, и выявить ключевые закономерности. В Python этот процесс можно автоматизировать с помощью таких библиотек, как Matplotlib, Seaborn и NumPy.
Чтобы начать работу с распределением данных, прежде всего нужно подготовить набор данных. Например, можно использовать функции из NumPy для создания случайных выборок из нормального распределения, чтобы моделировать поведение реальных данных. Функция numpy.random.normal() позволяет задать параметры среднего значения и стандартного отклонения, что важно для настройки симуляции распределений. Если данные уже есть, можно перейти к их визуализации.
Для построения графиков часто используется Matplotlib. Основные типы графиков для визуализации распределений включают гистограммы и плотности распределений. Гистограмму можно построить с помощью matplotlib.pyplot.hist(), где важно правильно выбрать количество бинов (размер интервалов), чтобы график не был слишком сглаженным или слишком «шумным». Для более точного отображения плотности распределения полезно использовать функцию seaborn.kdeplot(), которая создает гладкую кривую плотности, основываясь на данных.
При работе с распределениями важно учитывать, что для различных типов данных могут быть подходящими разные методы. Например, для числовых данных с нормальным распределением, помимо визуализации, стоит применить методы статистического тестирования, такие как тест Шапиро-Уилка для проверки нормальности. Использование инструментов из scipy.stats значительно улучшает качество анализа.
Как выбрать тип распределения для анализа данных в Python
После визуализации важно провести статистические тесты для подтверждения гипотезы о распределении. Для этого можно использовать Shapiro-Wilk test, Kolmogorov-Smirnov test или Anderson-Darling test, которые проверяют гипотезу о нормальности данных. Если данные не соответствуют нормальному распределению, следует рассматривать другие типы распределений.
Одним из распространённых вариантов является распределение Пуассона, которое используется для моделирования редких событий, происходящих за фиксированное время или в определённой области. Оно применимо, например, при анализе числа аварий на дороге или числа звонков в колл-центр за определённый период времени.
Если данные характеризуются длительными хвостами, то есть высокую вероятность экстремальных значений, лучше использовать распределение Парето или распределение Стьюдента. Эти распределения подходят для анализа финансовых данных, распределений доходов или иных экономических показателей, где редкие, но значительные события играют большую роль.
Для моделирования процессов с несколькими возможными исходами часто используется нормальное распределение, которое характеризуется симметричностью и хорошо подходит для большинства естественных явлений, таких как рост людей, ошибки измерений или другие случайные процессы с равномерной вероятностью появления значений в центре и их уменьшением по мере удаления от среднего.
В случае, когда распределение данных имеет дискретные значения, например, количество выигрышей в лотерее или число поломок на производстве, можно применить биномиальное распределение или распределение Бернулли. Эти распределения используются для анализа ситуаций с двумя возможными исходами: успех или неудача.
Для многоступенчатых или иерархических процессов подходит нормальное распределение с ограничениями или распределение Гамма, которое применимо, например, в анализе времени ожидания или количества товаров, производимых на фабрике.
Подытоживая, правильный выбор распределения зависит от особенностей данных и целей анализа. Для каждого типа распределения Python предлагает обширный набор библиотек, таких как scipy.stats, statsmodels, и PyMC3, которые могут помочь в расчёте параметров и проверке гипотез о распределении. Использование этих инструментов позволяет более точно подобрать модель для анализа и предсказания.
Использование библиотеки NumPy для генерации данных с распределением
Библиотека NumPy предоставляет мощные инструменты для генерации случайных данных с различными распределениями, что полезно для анализа, симуляций и тестирования алгоритмов. Рассмотрим, как можно генерировать данные для нескольких популярных типов распределений с помощью функции numpy.random.
Для нормального распределения используется функция numpy.random.normal. Она принимает три аргумента: среднее значение (mean), стандартное отклонение (standard deviation) и размер выборки (size). Пример:
import numpy as np
data = np.random.normal(loc=0, scale=1, size=1000)Этот код генерирует 1000 случайных чисел с нормальным распределением, где среднее значение равно 0, а стандартное отклонение – 1.
Для генерации данных с равномерным распределением применяется numpy.random.uniform. Этот метод требует указания диапазона значений (параметры low и high) и размера выборки:
data = np.random.uniform(low=0, high=10, size=1000)Здесь генерируются 1000 случайных значений в интервале от 0 до 10.
Для работы с распределением Пуассона используется функция numpy.random.poisson. Она принимает параметр λ (среднее количество событий) и размер выборки:
data = np.random.poisson(lam=5, size=1000)Этот код генерирует выборку из 1000 значений, соответствующих распределению Пуассона с λ = 5.
Если нужно работать с экспоненциальным распределением, можно использовать numpy.random.exponential. Параметр scale задает среднее значение, а size – размер выборки:
data = np.random.exponential(scale=1, size=1000)В данном примере генерируется выборка из 1000 значений с экспоненциальным распределением со средним значением 1.
Важно понимать, что NumPy позволяет не только генерировать данные, но и настраивать их характеристики, такие как среднее значение, дисперсию, диапазон и форму распределения. Используя эти функции, можно создать данные для тестирования моделей или для проведения различных симуляций.
Построение гистограммы распределения с помощью Matplotlib
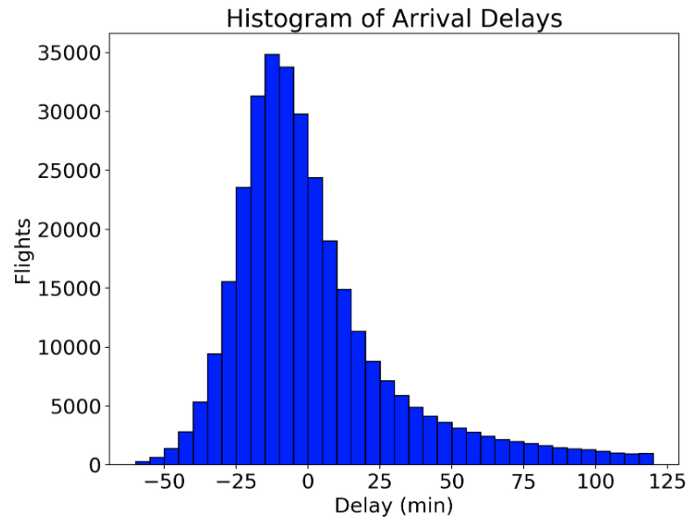
Для визуализации распределения данных в Python удобно использовать гистограмму. Matplotlib – один из самых популярных инструментов для этого. Гистограмма позволяет оценить, как часто встречаются различные диапазоны значений в наборе данных, делая информацию о распределении более наглядной.
Создание гистограммы в Matplotlib начинается с использования функции plt.hist(). В качестве входных данных можно передавать как одномерные массивы, так и наборы данных из pandas DataFrame. Основные параметры этой функции: bins (количество столбцов в гистограмме), range (диапазон значений), density (нормировка по площади). Например, для создания гистограммы с 10 столбцами по данным массива можно написать следующий код:
import matplotlib.pyplot as plt import numpy as np data = np.random.randn(1000) # Генерация случайных данных с нормальным распределением plt.hist(data, bins=10, density=True) plt.show()
В данном примере np.random.randn(1000) генерирует 1000 случайных данных с нормальным распределением. Параметр density=True нормирует гистограмму так, чтобы ее площадь была равна 1, что особенно полезно при сравнении распределений различных наборов данных.
Если необходимо настроить внешний вид гистограммы, можно использовать дополнительные параметры: color для цвета столбцов, edgecolor для цвета границ, alpha для прозрачности. Пример:
plt.hist(data, bins=15, color='blue', edgecolor='black', alpha=0.7) plt.show()
При работе с большими наборами данных, чтобы избежать переполнения визуализации, можно использовать параметр bins для увеличения точности или выбирать конкретные диапазоны данных с помощью range. Важно помнить, что слишком большое количество столбцов может затруднить восприятие распределения, поэтому нужно подобрать оптимальное значение для bins.
Для проверки нормальности распределения часто строят гистограмму с наложенной теоретической кривой плотности. Для этого можно использовать библиотеку seaborn или добавить кривую вручную с помощью scipy.stats. Пример с наложением кривой плотности:
import seaborn as sns sns.histplot(data, kde=True) plt.show()
Таким образом, гистограммы в Matplotlib позволяют эффективно визуализировать распределения данных и легко настраивать внешний вид графиков в соответствии с потребностями анализа.
Проверка данных на соответствие теоретическому распределению с SciPy
Для проверки того, насколько данные соответствуют определенному теоретическому распределению, в Python можно использовать библиотеку SciPy, которая предоставляет функции для статистических тестов и оценки параметров распределений.
Наиболее часто для этих целей используется тест Колмогорова-Смирнова (KS-тест), который позволяет сравнить эмпирическое распределение данных с теоретическим. В SciPy этот тест реализован в функции scipy.stats.kstest.
Пример использования:
import numpy as np
from scipy import stats
# Генерация данных, подчиняющихся нормальному распределению
data = np.random.normal(0, 1, 1000)
# Применение KS-теста для проверки на нормальность
statistic, p_value = stats.kstest(data, 'norm')
print(f"Статистика: {statistic}, p-значение: {p_value}")
Если p-значение больше 0.05, то гипотеза о том, что данные следуют нормальному распределению, не отвергается. В противном случае, если p-значение меньше 0.05, данные не соответствуют выбранному распределению.
Кроме KS-теста, в SciPy есть другие полезные функции для проверки соответствия данных распределению, например:
scipy.stats.normaltest– тест для нормальности (основан на коэффициентах асимметрии и эксцесса).scipy.stats.anderson– проверка на соответствие данным нормальному распределению с помощью статистики Андерсона.scipy.stats.chisquare– проверка на соответствие распределению хи-квадрат.
Для более сложных проверок можно использовать метод максимального правдоподобия для оценки параметров теоретического распределения и затем провести тесты на основе полученных параметров.
Пример применения теста Андерсона:
result = stats.anderson(data, dist='norm')
print(f"Статистика: {result.statistic}, Критические значения: {result.critical_values}")
Если статистика больше критического значения для заданного уровня значимости, то гипотеза о нормальности отклоняется. Это позволяет более гибко подходить к анализу распределений, особенно когда необходимо работать с несколькими типами распределений.
Важно отметить, что для практического использования рекомендуется предварительно визуализировать данные с помощью гистограммы или графика плотности, чтобы предварительно оценить, насколько они могут соответствовать теоретическому распределению.
Как анализировать отклонения от нормального распределения с помощью статистики
1. Визуализация данных
- Гистограмма: Плотность распределения данных можно оценить с помощью гистограммы. Если данные близки к нормальному распределению, гистограмма должна напоминать колокол.
- Квантиль-квантильный график (Q-Q plot): Это график, на котором сравниваются квантели выборки с квантелями нормального распределения. Отклонения от прямой линии указывают на отклонения от нормальности.
- Ящик с усами (Boxplot): Визуализирует выбросы и распределение данных, что также может помочь оценить отклонения от нормальности.
2. Статистические тесты
- Тест Шапиро-Уилка: Это один из самых популярных тестов для проверки нормальности данных. Если p-значение меньше 0.05, данные отклоняются от нормального распределения.
- Тест Колмогорова-Смирнова: Проверяет согласие распределения выборки с нормальным распределением. Он основан на максимальном различии между эмпирической функцией распределения и теоретической.
- Тест Андерсона-Дарлинга: Еще один мощный инструмент для тестирования нормальности, который предоставляет более точные результаты, чем другие тесты для небольших выборок.
3. Коэффициент асимметрии и куртозиса
- Асимметрия: Измеряет отклонение распределения от симметрии. Для нормального распределения асимметрия должна быть близка к 0. Значения выше 0 указывают на правостороннюю асимметрию, ниже 0 – на левостороннюю.
- Куртозис: Оценка «остроты» распределения. Куртозис нормального распределения равен 3. Значения выше 3 говорят о более острых пиках, ниже – о более плоском распределении.
4. Выбросы и их влияние
- Отклонения от нормальности часто происходят из-за выбросов, которые искажают статистику. Для их обнаружения можно использовать межквартильный размах (IQR) или стандартные отклонения.
- При анализе данных важно учитывать, как выбросы могут повлиять на тесты нормальности. В некоторых случаях имеет смысл исключить выбросы или использовать робастные методы оценки.
5. Преобразования данных
- Для коррекции отклонений от нормальности часто используют логарифмическое, квадратное или коробочное преобразование. Эти методы могут сделать распределение более близким к нормальному, что улучшит качество анализа.
- Перед применением преобразований всегда проверяйте их эффективность, используя тесты нормальности и визуализацию.
Создание плотности вероятности с использованием seaborn для визуализации

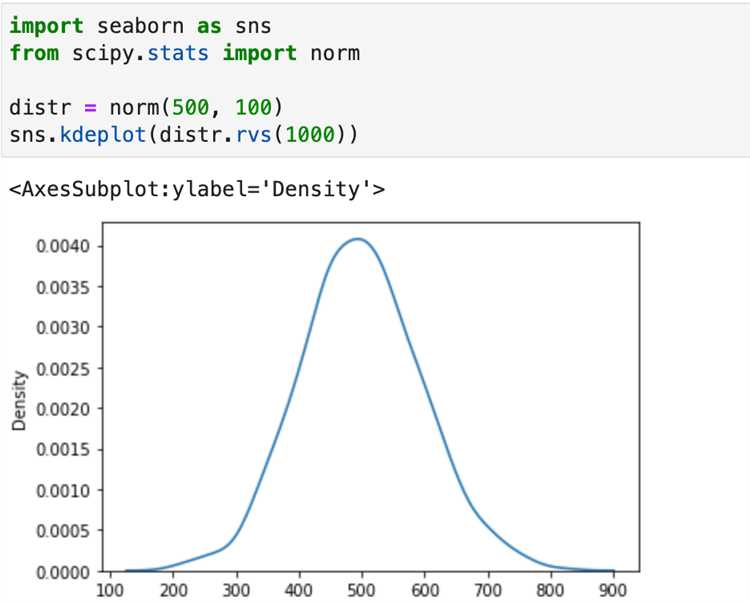
Основной параметр функции – это набор данных, для которого строится плотность. seaborn.kdeplot() автоматически подбирает оптимальные параметры для плотности на основе данных, но вы можете настроить ее под свои требования, изменяя параметры, такие как bw_adjust, который регулирует сглаживание кривой плотности, и shade, который позволяет заполнить пространство под графиком.
Пример простого использования:
import seaborn as sns
import matplotlib.pyplot as plt
data = sns.load_dataset('iris')['sepal_length']
sns.kdeplot(data)
plt.show()В этом примере используется набор данных из библиотеки seaborn для длины чашелистика в цветке ириса. График плотности отображает, как данные распределены, с плавной кривой, указывающей на участки с наибольшей вероятностью появления значений.
Если вы хотите добавить несколько плотностей на один график, можно передать несколько наборов данных:
data1 = sns.load_dataset('iris')['sepal_length']
data2 = sns.load_dataset('iris')['petal_length']
sns.kdeplot(data1, label='Sepal Length')
sns.kdeplot(data2, label='Petal Length')
plt.legend()
plt.show()Визуализация нескольких плотностей помогает выявить различия в распределениях различных переменных. Можно также изменить стиль отображения кривой с помощью параметра linestyle или цвета с помощью color.
Важно: для корректного отображения плотности важно понимать, что она не обязательно будет представлять форму нормального распределения. Плотность может принимать различные формы в зависимости от структуры ваших данных.
Для более точного представления данных можно использовать параметр fill для закрашивания области под графиком:
sns.kdeplot(data1, shade=True, color="blue")
sns.kdeplot(data2, shade=True, color="red")
plt.show()Визуализация плотности с заполнением помогает лучше воспринимать данные, особенно когда нужно сравнивать несколько распределений. Использование seaborn для этих целей значительно улучшает читабельность и наглядность графиков, а также делает код более компактным и понятным.
Вопрос-ответ:
Что такое распределение данных и зачем его строить в Python?
Распределение данных — это способ организации информации, который помогает понять, как значения переменных распределяются по диапазону. Это позволяет выявить закономерности, тенденции и аномалии в данных. В Python для визуализации распределений чаще всего используют такие библиотеки, как Matplotlib и Seaborn. Построение распределений важно для анализа данных, так как это помогает корректно выбирать методы статистической обработки и предсказания.