Как сравнить double java

При сравнении чисел с плавающей запятой в Java существует ряд особенностей, которые могут привести к ошибкам из-за ограниченной точности представления таких значений. Тип данных double используется для хранения вещественных чисел, но из-за природы этого типа, точность представления может быть неидеальной. Стандартные операторы сравнения (например, ==) могут не дать корректного результата, если значения не совпадают точно, но находятся на очень близком расстоянии друг от друга.

Для корректного сравнения значений double рекомендуется использовать подход с погрешностью. Погрешность указывает на максимально допустимую разницу между числами, при которой они считаются равными. Это особенно важно при работе с результатами вычислений, где округление и ошибки представления неизбежны. Для этого существует несколько методов, включая использование библиотеки Math.abs() для вычисления разницы между числами и её сравнение с заранее заданной константой, называемой порогом точности.

Пример правильного сравнения чисел типа double в Java выглядит следующим образом:

double a = 0.1 + 0.2; double b = 0.3; double epsilon = 1e-9; if (Math.abs(a - b) < epsilon) { // Числа считаются равными }

Важно понимать, что значение epsilon должно быть выбрано в зависимости от контекста задачи. Для некоторых приложений достаточно небольшой погрешности (например, 1e-6), в то время как для научных расчетов может потребоваться более строгий порог.

Использование оператора == для сравнения double в Java

Оператор == в Java используется для проверки, равны ли два значения. Однако при сравнении типов данных с плавающей точкой, таких как double, результат может быть неожиданным. Это связано с особенностями представления чисел с плавающей точкой в памяти.

Числа типа double хранятся в формате IEEE 754, который не всегда точно отражает десятичные значения из-за ограниченной точности представления. Например, выражения типа 0.1 + 0.2 == 0.3 могут возвращать false, несмотря на то, что математически это верно. Это происходит из-за того, что числа с плавающей точкой в компьютере часто имеют небольшие погрешности при представлении.

Для правильного сравнения значений типа double следует использовать подход с заданием погрешности, иначе простое использование == может привести к неправильным результатам. Рекомендуется вместо этого проверять, насколько разница между двумя числами меньше заданного порога (epsilon). Например:

double a = 0.1 + 0.2;
double b = 0.3;
double epsilon = 1e-9;
if (Math.abs(a - b) < epsilon) {
System.out.println("Числа равны");
} else {
System.out.println("Числа не равны");
}

В этом примере разница между a и b проверяется на величину, которая меньше заданного значения epsilon. Такой подход позволяет избежать ошибок, связанных с точностью представления чисел в памяти.

Использование оператора == возможно только в случаях, когда значения сравниваемых переменных гарантированно имеют одинаковую точность. Например, если значения числа double получены в результате каких-то вычислений с фиксированными параметрами, и вы уверены, что погрешности в процессе вычислений исключены.

Важно помнить, что в случае с double нужно всегда учитывать возможность ошибок округления и использовать погрешности для корректного сравнения чисел.

Как избежать ошибок при сравнении значений double с использованием погрешности

При сравнении значений типа double в Java необходимо учитывать погрешности, возникающие из-за особенностей представления чисел с плавающей точкой. Эти погрешности могут привести к некорректным результатам при прямом сравнении значений с использованием оператора ==.

Для корректного сравнения рекомендуется использовать подход с допустимой погрешностью (эпсилон). Это позволяет определить, насколько два числа близки друг к другу в пределах заданной точности, и избежать ошибок при сравнении. Вместо того чтобы проверять равенство чисел, следует проверять, что их разница меньше некоторого заранее определённого значения.

Пример правильного сравнения:

double a = 0.1 + 0.2;
double b = 0.3;
double epsilon = 1e-9;
if (Math.abs(a - b) < epsilon) {
System.out.println("Числа равны с учётом погрешности");
}

В данном примере разница между значениями a и b сравнивается с малым числом epsilon, которое отражает допустимую погрешность. Это позволяет избежать ошибок, связанных с точностью вычислений при представлении чисел с плавающей точкой.

Выбор значения для epsilon зависит от контекста задачи. Если точность требуется высокая, epsilon должно быть меньшим. Например, для финансовых расчетов можно использовать epsilon = 1e-6, а для научных вычислений – значения порядка 1e-15.

Также важно помнить, что ошибка при сравнении может возникнуть из-за накопления погрешностей в последовательных вычислениях. В таких случаях следует пересматривать алгоритмы и минимизировать количество операций с плавающей точкой.

Методы сравнения с учетом точности: использование Math.abs() и других подходов

В Java, при сравнении значений типа double, важно учитывать погрешности, возникающие из-за особенностей представления чисел с плавающей запятой. Прямое сравнение таких значений с помощью оператора "==" может привести к ошибкам, поскольку даже незначительные изменения в значении могут быть результатом ошибок округления. Для корректного сравнения используется подход с учетом точности, где погрешности ограничиваются заранее заданным порогом.

Одним из самых распространенных методов является использование функции Math.abs(). Суть метода заключается в том, чтобы сравнивать разницу между двумя числами с минимальным порогом ошибок, а не их точные значения. Обычно сравнение осуществляется так: если абсолютное значение разницы между числами меньше заданной точности, то числа считаются равными.

Пример использования:

double a = 0.1 + 0.2;
double b = 0.3;
double epsilon = 1e-9;
if (Math.abs(a - b) < epsilon) {
System.out.println("Числа равны с учетом погрешности");
} else {
System.out.println("Числа не равны");
}

В данном примере разница между переменными a и b оценивается с учетом небольшой погрешности (epsilon). Если разница меньше epsilon, числа считаются равными, несмотря на возможные ошибки округления при вычислениях.

Другим вариантом является использование метода Double.compare(), который позволяет избежать ошибок, связанных с прямым сравнением. Он возвращает 0, если числа равны, отрицательное значение, если первое число меньше второго, и положительное, если первое больше второго. Этот метод полезен при необходимости сортировки или при работе с коллекциями, где важно корректно определить порядок чисел с учетом погрешностей.

Также стоит упомянуть подходы с использованием комбинированных методов, например, сравнение чисел по степени их близости с заранее заданными порогами. В таких случаях для точности можно учитывать не только абсолютное значение разницы, но и относительную разницу, что особенно важно при работе с очень большими или очень маленькими числами.

Кроме Math.abs(), часто используются другие математические методы для контроля точности: Math.nextUp() и Math.nextDown() позволяют контролировать направление округления и минимизировать погрешности при вычислениях. Эти методы полезны, например, когда нужно точно контролировать, как числа округляются к ближайшему возможному значению в рамках операций с плавающей запятой.

Преимущества и недостатки использования BigDecimal для сравнения значений double

Использование класса BigDecimal в Java для сравнения значений типа double позволяет избежать проблем, связанных с погрешностями представления чисел с плавающей запятой. Однако такая практика имеет свои плюсы и минусы, которые важно учитывать при принятии решения о применении этого класса.

Основным преимуществом является высокая точность, которую предоставляет BigDecimal. Этот класс поддерживает произвольную точность и исключает погрешности, которые неизбежно возникают при работе с типом double, например, при делении или сравнении значений, близких к нулю. BigDecimal выполняет арифметические операции с заданным количеством знаков после запятой, что делает его идеальным инструментом для финансовых расчетов или задач, где важна точность.

Однако использование BigDecimal также имеет недостатки. Во-первых, операции с этим классом гораздо медленнее, чем с примитивными типами данных. Каждая операция требует создания нового объекта, что может привести к значительным накладным расходам при большом объеме вычислений. Во-вторых, для сравнения значений BigDecimal необходимо учитывать не только значения чисел, но и их точность, что делает код более сложным и менее читаемым.

При сравнении значений double через BigDecimal важно учитывать, что это не всегда оправдано. Если задача не требует высокой точности, использование BigDecimal может быть излишним и привести к неоправданным затратам на производительность. В таких случаях более подходящим решением является использование встроенных методов для сравнения значений double с определенной погрешностью, например, с использованием метода Math.abs() для проверки разницы между числами.

Таким образом, использование BigDecimal для сравнения double оправдано только в случаях, когда точность действительно критична. Для большинства других случаев предпочтительнее применять стандартные средства Java для работы с числами с плавающей запятой, чтобы избежать лишней сложности и потерь в производительности.

Сравнение double при работе с числами с плавающей точкой в финансовых приложениях

При разработке финансовых приложений важность точности вычислений и корректности сравнения чисел с плавающей точкой невозможно переоценить. В Java тип данных double используется для представления чисел с плавающей точкой, однако он имеет ограничения, которые могут привести к погрешностям при операциях с денежными величинами.

Основная проблема заключается в том, что числа с плавающей точкой не всегда могут быть представлены точно в двоичной системе. Например, такие числа как 0.1 или 0.2 не могут быть точно записаны в двоичном представлении, что приводит к небольшим погрешностям. В финансовых приложениях даже минимальные отклонения могут вызвать ошибку в расчётах. Поэтому для сравнения значений типа double рекомендуется использовать подходы, которые минимизируют такие погрешности.

Один из способов избежать ошибок – использовать метод сравнения с заданной точностью. Для этого можно вычислять разницу между числами и сравнивать её с маленьким значением, называемым "погрешностью" или "эпсилоном". Например, для сравнения двух чисел a и b, можно использовать следующую формулу:

double epsilon = 0.00001;
if (Math.abs(a - b) < epsilon) {
// a и b считаются равными
}

Такой подход позволяет учитывать погрешности, возникающие из-за ограничений представления чисел с плавающей точкой в памяти компьютера.

Кроме того, для работы с деньгами в финансовых приложениях часто используется класс BigDecimal, который позволяет точно представлять дробные значения, избегая проблем с точностью, присущих double. Этот класс поддерживает произвольную точность и предоставляет методы для точных арифметических операций и сравнения чисел, что делает его более предпочтительным для финансовых расчётов.

Когда необходимо использовать double для числовых вычислений, важно учитывать контекст задачи и ограничивать погрешности, применяя методы округления и установление допустимой погрешности при сравнении. Для финансовых операций всегда следует учитывать специфику представления чисел с плавающей точкой и при необходимости заменять их на более точные типы данных, такие как BigDecimal.

Практические ошибки при сравнении double и как их избежать

Сравнение значений типа double в Java может привести к непредсказуемым результатам из-за особенностей представления чисел с плавающей запятой в памяти. Рассмотрим распространенные ошибки и способы их избежать.

Ошибка: использование оператора "==" для сравнения значений double

Рекомендация: Вместо оператора == используйте подход с заданием точности через разницу между значениями и допустимой погрешностью.

Ошибка: неверно выбранный порог для сравнения

Еще одной ошибкой является неправильный выбор значения погрешности при сравнении чисел с плавающей запятой. Если погрешность слишком велика, сравнение может привести к ложным результатам, если слишком мала – возможно, не будет заметна даже допустимая разница.

Рекомендация: Обычно используется небольшое значение, например 1e-15, но его выбор зависит от контекста задачи. Например, для финансовых расчетов погрешность может быть больше, чем для научных вычислений.

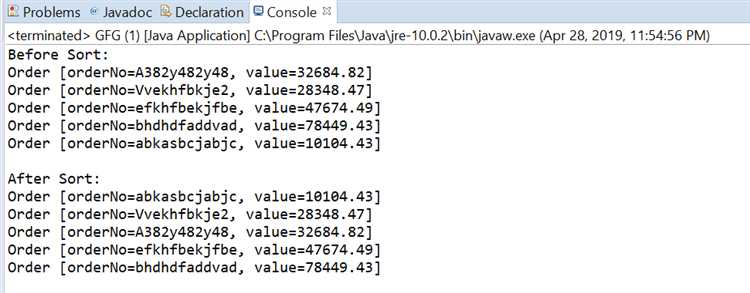
Ошибка: сравнение чисел с различными масштабами

Когда сравниваются значения с разными порядками величин, даже если их абсолютная разница маленькая, они могут восприниматься как равные или разные в зависимости от масштаба. Например, числа 1.000000000000001 и 1.0 могут быть посчитаны равными при использовании недостаточно точной погрешности.

Рекомендация: Перед сравнением чисел приведите их к одинаковой точности или масштабу. Можно использовать логарифмические сравнения, если числа находятся в разных порядках.

Ошибка: игнорирование возможности NaN и Infinity

Необходимо учитывать, что значения double могут быть представлены как NaN (Not a Number) или Infinity, которые не равны никаким другим числам, включая сами себя. Это может вызвать сбои в логике программы, если не предусмотреть такие случаи.

Рекомендация: Для обработки NaN используйте метод Double.isNaN(), а для проверки на бесконечность – Double.isInfinite().

Ошибка: использование округления в процессе вычислений

Часто в процессе вычислений возникает необходимость округлить число, но округление может искажать результаты, особенно если оно выполняется не с учетом точности чисел с плавающей запятой.

Рекомендация: Не округляйте значения до окончательного сравнения. Лучше сравнивать числа с плавающей запятой на основе их абсолютной разницы, без промежуточных округлений.

Ошибка: отсутствие тестов на крайние значения

Часто при тестировании программ забывают проверять крайние значения типа double, такие как Double.MAX_VALUE, Double.MIN_VALUE, -Double.MAX_VALUE, а также NaN и Infinity. Это может привести к багам, которые трудно заметить при обычных тестах.

Рекомендация: Проводите тестирование с использованием крайних значений и убедитесь, что ваше приложение корректно обрабатывает все возможные ситуации с числами с плавающей запятой.

Вопрос-ответ:

Как правильно сравнивать значения double в Java?

При сравнении значений типа double в Java важно учитывать особенности представления чисел с плавающей точкой. Числа типа double могут терять точность из-за ограничений в представлении значений в памяти. Поэтому, чтобы избежать ошибок при сравнении, не следует использовать операторы "==" или "!=" для точного сравнения значений типа double. Вместо этого рекомендуется использовать подход с допустимой погрешностью. Это можно сделать с помощью метода `Math.abs(a - b) < epsilon`, где `epsilon` — это небольшая величина, которая указывает на допустимую погрешность сравнения. Этот подход позволяет учесть возможные погрешности при представлении чисел в памяти и корректно сравнивать их.

Что такое допустимая погрешность при сравнении чисел типа double в Java?

Допустимая погрешность (или `epsilon`) — это минимальное значение, которое учитывается при сравнении двух чисел с плавающей точкой, таких как double, чтобы понять, что числа "равны" друг другу, несмотря на возможные незначительные различия из-за точности вычислений. Например, при сравнении чисел 1.0000001 и 1.0000002 в Java можно использовать небольшой коэффициент, например, `epsilon = 0.000001`, чтобы считать эти числа равными. Выбор значения `epsilon` зависит от требуемой точности для конкретной задачи, однако слишком большое значение может привести к ошибочным результатам, а слишком маленькое — к проблемам с производительностью.

Почему нельзя использовать оператор "==" для сравнения double в Java?

Оператор "==" в Java сравнивает два значения точно, и это может вызвать ошибки при сравнении чисел типа double. Причина в том, что числа с плавающей запятой (например, double) не всегда могут быть представлены с абсолютной точностью из-за ограничений в машинном представлении чисел. Например, выражение `0.1 + 0.2` может не быть точно равно `0.3` из-за особенностей представления этих чисел в памяти. В таких случаях "==" может вернуть false, даже если числа по сути равны, если их отличие меньше допустимой погрешности. Поэтому для сравнения чисел типа double рекомендуется использовать метод с проверкой на допустимую погрешность, как описано выше.

Как выбрать значение погрешности (epsilon) при сравнении чисел типа double?

Значение погрешности (epsilon) при сравнении чисел типа double выбирается в зависимости от того, насколько точным должно быть ваше сравнение и какие ограничения накладывает ваша задача. Для большинства практических приложений обычно выбирают epsilon в пределах от 10^-6 до 10^-12. Например, если ваша задача не требует высокой точности, можно использовать значение epsilon в 0.000001, что достаточно для большинства случаев. Для задач, где точность имеет критическое значение (например, в научных расчетах), следует использовать более мелкие значения epsilon. Важно не выбирать слишком маленькое значение, так как это может привести к ошибкам из-за накопления погрешностей при вычислениях.