Как распечатать только диагональ матрицы matlab

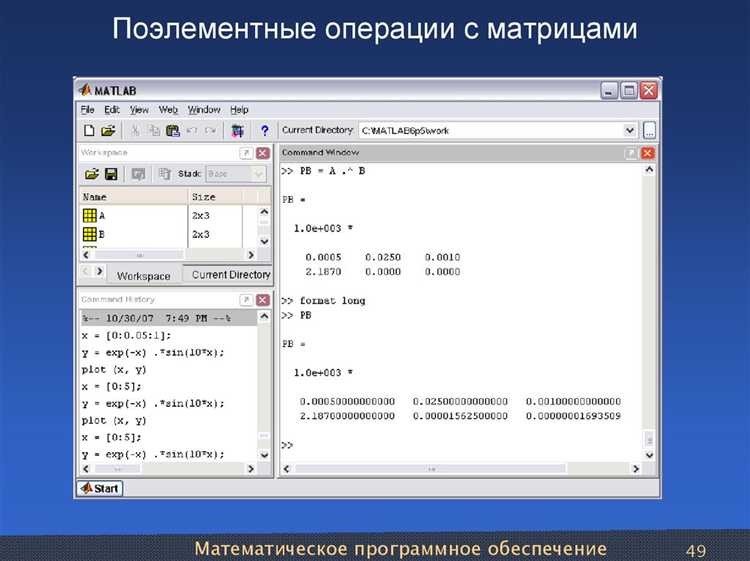
В MATLAB работа с матрицами реализована на низком уровне, что позволяет эффективно извлекать как главную, так и побочные диагонали. Основная функция для получения диагональных элементов – diag. Она возвращает вектор диагонали или формирует диагональную матрицу из заданного вектора. Например, diag(A) извлекает главную диагональ матрицы A, тогда как diag(A, k) позволяет получить диагональ, смещённую на k позиций относительно главной.

Для квадратной матрицы размером n × n функция diag(A) вернёт вектор длины n, содержащий элементы A(i,i). При положительном смещении k будут возвращены элементы выше главной диагонали – A(i,i+k), при отрицательном – элементы ниже неё: A(i-k,i). Это позволяет точно управлять выбором нужной диагонали без использования циклов.

Если требуется вывести диагональ в консоль, используйте конструкцию disp(diag(A)). Для программной обработки удобно сохранять результат в переменную: d = diag(A). В случае нестандартных требований, например, извлечения диагонали из подматрицы или работы с трёхмерными массивами, применяется индексирование: A(1:n+1:end) – быстрый способ получить главную диагональ без вызова diag.

Знание этих приёмов критично при решении задач линейной алгебры, численного моделирования и оптимизации в MATLAB, где точность и лаконичность кода имеют первостепенное значение.

Как извлечь главную диагональ квадратной матрицы с помощью функции diag

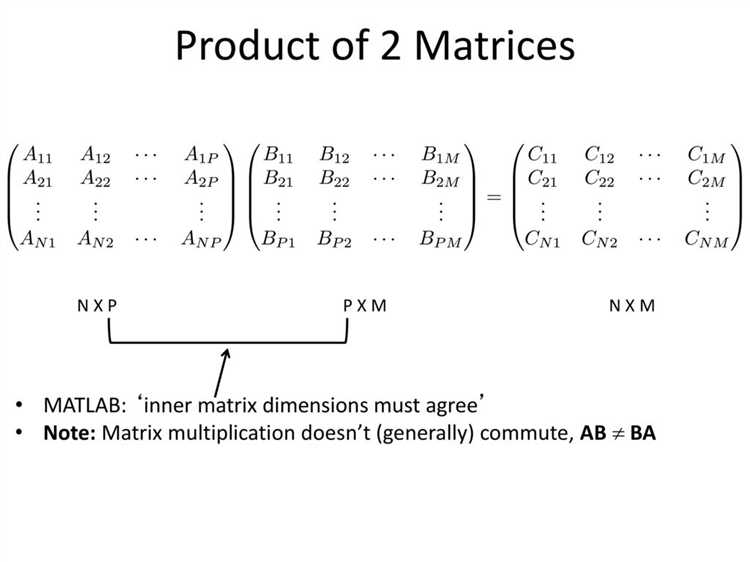
Для получения главной диагонали квадратной матрицы в MATLAB используется встроенная функция diag. Если задана матрица A размером n × n, то выражение diag(A) вернёт столбец из n элементов, содержащий значения с позиций A(i, i) для i = 1, 2, ..., n.

Пример: пусть A = [4 2 7; 1 5 9; 3 8 6]. Тогда diag(A) вернёт вектор [4; 5; 6].

Результат всегда представляет собой вектор-столбец. Если требуется сохранить форму строки, используйте транспонирование: diag(A)ʼ.

Функция diag применима только к числовым или логическим матрицам. При работе с символьными матрицами требуется предварительная проверка формата данных. В случае использования матриц с комплексными элементами диагональные значения сохраняют свою комплексную часть без изменений.

Если передать diag вектор, функция создаст диагональную матрицу, что часто используется для последующего анализа, но в рамках извлечения диагонали следует передавать двумерную матрицу.

Получение побочной диагонали через индексацию и преобразование матрицы

Для извлечения побочной диагонали квадратной матрицы в MATLAB, достаточно инвертировать порядок столбцов и применить функцию diag. Пусть задана матрица A размером n × n. Побочная диагональ содержит элементы A(i, n - i + 1) для i = 1:n.

Оптимальный способ – отразить матрицу по вертикали: B = fliplr(A). После этого главная диагональ B соответствует побочной диагонали A. Извлечение осуществляется вызовом diag(fliplr(A)), что возвращает вектор нужных элементов без явного цикла.

Альтернативный способ – использовать линейную индексацию. Побочная диагональ матрицы A размера n находится по индексам (1:n) + (n:-1:1 - 1) * n. Пример: diag_elements = A(sub2ind(size(A), 1:n, n:-1:1)). Этот подход особенно полезен при работе с большим числом матриц внутри вектора или ячеек.

Рекомендуется избегать циклов при извлечении диагоналей: они увеличивают время выполнения на больших массивах. Использование встроенных функций diag, fliplr и sub2ind обеспечивает краткость и производительность.

Извлечение диагонали из прямоугольной матрицы

В MATLAB функция diag позволяет извлекать элементы диагонали даже из прямоугольных матриц. При этом учитываются только те элементы, которые лежат на пересечении соответствующих строк и столбцов, образующих диагональ.

Пусть дана матрица A размером 3×5:

A = [1  2  3  4  5;
6  7  8  9 10;
11 12 13 14 15];

Основная диагональ определяется вызовом:

d = diag(A);

Результат: d = [1; 7; 13]. Элементы берутся из позиций (1,1), (2,2), (3,3). Выход за пределы по строкам или столбцам игнорируется.

Для извлечения наддиагонали (смещённой вверх на k позиций), указывайте положительное значение смещения:

d = diag(A, 1);

Результат: d = [2; 8; 14] – элементы (1,2), (2,3), (3,4).

Аналогично, поддиагональ извлекается с отрицательным смещением:

d = diag(A, -1);

Результат: d = [6; 12] – позиции (2,1), (3,2).

При работе с прямоугольными матрицами учитывайте размерности: максимальное допустимое смещение ограничено так, чтобы индексы не выходили за границы. Это можно проверить через:

[m, n] = size(A);
max_k = n - 1;
min_k = -m + 1;

Для создания вектора всех доступных диагоналей используйте цикл:

for k = -m+1:n-1
d = diag(A, k);
% Обработка диагонали d
end

Формирование диагональной матрицы из вектора

Для создания диагональной матрицы в MATLAB на основе одномерного вектора применяется функция diag. Вектор должен быть строкой или столбцом, содержащим значения, которые необходимо разместить на главной диагонали результирующей матрицы.

Синтаксис: D = diag(v), где v – вектор, а D – диагональная матрица.
Если v – вектор длины n, то D будет квадратной матрицей размера n×n с элементами v(i) на позиции (i,i).
Нули автоматически заполняют все недиагональные элементы матрицы.

Примеры:

v = [3, 5, 7]; D = diag(v); – создаст матрицу [3 0 0; 0 5 0; 0 0 7].
v = (1:4)'; D = diag(v); – для столбцового вектора результат аналогичен: [1 0 0 0; 0 2 0 0; 0 0 3 0; 0 0 0 4].

Чтобы поместить вектор на побочную диагональ (выше или ниже главной), используется второй аргумент:

diag(v, k) – k > 0 размещает вектор выше главной диагонали, k < 0 – ниже.
Пример: diag([1 2 3], 1) создаёт матрицу с элементами 1, 2, 3 на первой наддиагонали.

Для многократного формирования диагональных матриц из разных векторов внутри цикла можно использовать прединициализацию массива с помощью zeros и индексную вставку с diag:

n = 5;
A = zeros(n);
v = 1:n;
A = A + diag(v);

Функция diag также поддерживает извлечение диагоналей из существующих матриц, но в контексте формирования она остаётся основным инструментом.

Как получить все диагонали матрицы, включая над- и поддиагонали

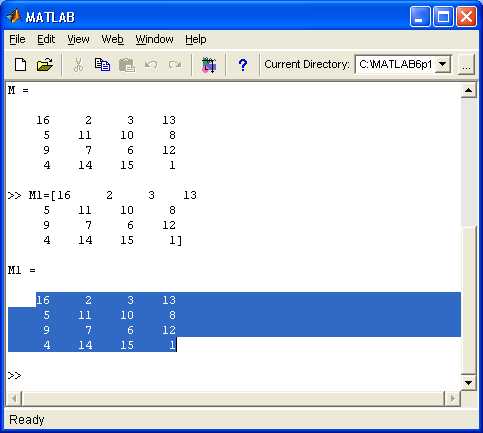
В MATLAB для извлечения всех диагоналей матрицы, включая главную, над- и поддиагонали, применяется функция diag в цикле с различными смещениями. Смещение указывается вторым аргументом и определяет, какую именно диагональ извлечь: положительное – наддиагональ, отрицательное – поддиагональ.

Пусть A – прямоугольная матрица размером m × n. Число всех диагоналей будет m + n - 1. Главная диагональ соответствует смещению 0. Максимальное положительное смещение – n - 1, минимальное отрицательное – -(m - 1).

Пример получения всех диагоналей:

for k = -(size(A,1)-1):(size(A,2)-1)
d = diag(A, k);
disp(['Диагональ со смещением ', num2str(k), ': ', mat2str(d')]);
end

Если необходимо сохранить все диагонали в виде массива, используйте cell-массив:

diagonals = cell(1, size(A,1)+size(A,2)-1);
index = 1;
for k = -(size(A,1)-1):(size(A,2)-1)
diagonals{index} = diag(A, k);
index = index + 1;
end

Таким образом, каждая диагональ будет храниться отдельно, что упрощает доступ и модификацию данных.

Сохранение диагональных элементов в отдельную переменную

Для извлечения главной диагонали квадратной или прямоугольной матрицы в MATLAB используйте функцию diag. Например, если задана матрица A, выражение d = diag(A); сохранит диагональные элементы в переменную d в виде столбцового вектора.

Если требуется сохранить диагональ, параллельную главной, укажите смещение вторым аргументом. diag(A, 1) извлечёт диагональ выше главной, diag(A, -1) – ниже. Полученный вектор можно использовать в дальнейших вычислениях без необходимости дополнительной обработки.

Для сохранения диагонали из матрицы с динамическими размерами рекомендуется использовать проверку: min(size(A)). Это позволяет гарантировать корректное извлечение при изменении входных данных: d = diag(A(1:min(size(A)), 1:min(size(A))));.

При формировании матрицы с заданной диагональю обратно используйте diag(d) – она создаст диагональную матрицу, где d выступает вектором значений. Это часто применимо при генерации матриц весов или масок.

Визуализация диагональных элементов на графике

Для наглядного отображения диагональных элементов матрицы в MATLAB удобно использовать функции построения графиков. Один из распространённых вариантов – построение линейного графика значений главной диагонали.

Создайте матрицу. Например: A = randi(100, 10, 10);
Извлеките главную диагональ: D = diag(A);
Постройте график: plot(D, '-o')

Для повышения информативности графика:

Добавьте сетку: grid on
Укажите подписи осей: xlabel('Индекс элемента'), ylabel('Значение')
Добавьте заголовок: title('Главная диагональ матрицы A')

Для визуализации побочных диагоналей используйте аргумент смещения в функции diag:

Верхняя побочная диагональ: D1 = diag(A, 1);
Нижняя побочная диагональ: D2 = diag(A, -1);

При отображении нескольких диагоналей на одном графике:

Используйте hold on перед вторым plot
Назначайте различные маркеры и цвета: plot(D1, '--s', 'Color', 'r')
Добавьте легенду: legend('Главная', 'Верхняя побочная')

Для двумерной визуализации используйте логическую маску:

Создайте маску: M = eye(size(A));
Получите диагональные значения: D = A .* M;
Отобразите: imagesc(D), colorbar

Если нужно выделить диагональ на фоне всей матрицы:

Отобразите всю матрицу: imagesc(A)
Наложите поверх диагональные значения с помощью text и циклов

Пример добавления текста:


for i = 1:min(size(A))
text(i, i, num2str(A(i,i)), 'Color', 'w', 'HorizontalAlignment', 'center');
end

Такой подход позволяет наглядно анализировать распределение диагональных элементов в контексте всей матрицы.