Как решать в программе mathematica

Mathematica предоставляет полноценную среду для аналитического и численного решения задач, объединяя символьные вычисления, визуализацию и программирование. В отличие от традиционных языков, она использует унифицированную символьную структуру выражений, что позволяет работать с математическими объектами в их естественном виде.

Для решения уравнений используется функция Solve для аналитического подхода и NSolve – для численного. Например, выражение Solve[x^2 + 3 x — 4 == 0, x] вернёт точные корни квадратного уравнения. При работе с системами уравнений удобно использовать списки и указывать переменные явно, чтобы избежать неоднозначностей.

Дифференциальные уравнения решаются с помощью DSolve и NDSolve. Первая возвращает общее решение в символьной форме, вторая – численное решение, пригодное для построения графиков и анализа поведения. При решении краевых задач важно правильно задать граничные условия в виде уравнений внутри списка.

Визуализация функций осуществляется с помощью Plot, ParametricPlot, ContourPlot и других команд. Для трёхмерной графики применяются Plot3D и ParametricPlot3D. Использование опций Mesh, ColorFunction и PlotRange позволяет адаптировать графики под конкретные исследовательские цели.

Для оптимизации выражений Mathematica предлагает Minimize, Maximize, NMinimize и NMaximize. В задачах с ограничениями переменные и условия указываются в явном виде в списке. Работа с многомерными функциями возможна без дополнительных библиотек, что делает Mathematica особенно эффективной для задач математического моделирования.

Пошаговое решение уравнений с использованием функции Solve

1. Ввод уравнения

Функция Solve применяется к уравнению или системе уравнений в виде Solve[уравнение, переменная]. Например, для уравнения x^2 - 4 == 0 ввод будет следующим:

Solve[x^2 - 4 == 0, x]

2. Анализ результата

Функция возвращает список правил замены в виде {{x -> -2}, {x -> 2}}. Каждый элемент списка представляет отдельное решение. Результаты можно использовать напрямую, подставляя через ReplaceAll (/. ).

3. Система уравнений

Для решения нескольких уравнений используется список: Solve[{x + y == 3, x - y == 1}, {x, y}]. Mathematica вернёт список решений, например: {{x -> 2, y -> 1}}.

4. Условные решения

5. Ограничение области решения

Для решения в области вещественных или целых чисел применяется опция Reals или Integers: Solve[x^2 + 1 == 0, x, Reals] вернёт пустой список, так как действительных корней нет.

6. Работа с неявными уравнениями

Для уравнений, где переменная не может быть явно выражена, Solve может не дать ответа. В таких случаях применяется Reduce, который возвращает логическое выражение, описывающее все решения.

7. Практика подстановки

Результат функции Solve можно сразу использовать: expr /. Solve[eq, x]. Это позволяет быстро получить численные или символьные значения для дальнейших вычислений.

8. Проверка решения

Используйте FullSimplify[уравнение /. решение], чтобы убедиться, что решение действительно обращает уравнение в тождество.

Численные методы для систем нелинейных уравнений через NSolve и FindRoot

NSolve применяется для численного поиска всех решений системы алгебраических уравнений. Метод эффективен при работе с конечными системами, где количество уравнений совпадает с числом переменных. Например:

NSolve[{x^3 + y^2 == 1, Sin[x] - y == 0}, {x, y}]

Команда возвращает список всех комплексных и вещественных корней, удовлетворяющих системе. Для ограничения решения только вещественными числами, добавьте условие Element[x|y, Reals]. NSolve использует символьные преобразования, переходя к численной оценке на финальном этапе. Он подходит, если предполагается наличие нескольких решений.

FindRoot предназначен для поиска одного численного корня, начиная с заданной начальной точки. Метод реализует модифицированные алгоритмы Ньютона и секущей. Пример:

FindRoot[{x^3 + y^2 == 1, Sin[x] - y == 0}, {{x, 0.5}, {y, 0.5}}]

Важно тщательно выбирать начальные приближения: близость к реальному корню критична для сходимости. FindRoot не гарантирует нахождение всех решений и не решает символически – только численно.

При работе с жёсткими или сильно нелинейными системами, увеличьте точность с помощью опций WorkingPrecision, AccuracyGoal, PrecisionGoal. Например:

FindRoot[{Exp[x] + y == 5, Log[y] - x == 1}, {{x, 1}, {y, 2}}, WorkingPrecision -> 30]

Если система неявно зависит от параметров, используйте ParametricNDSolve для численного анализа поведения корней при изменении параметров, комбинируя с FindRoot внутри цикла.

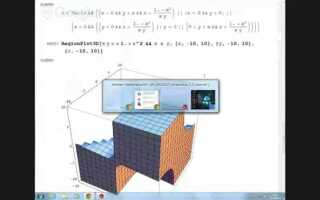
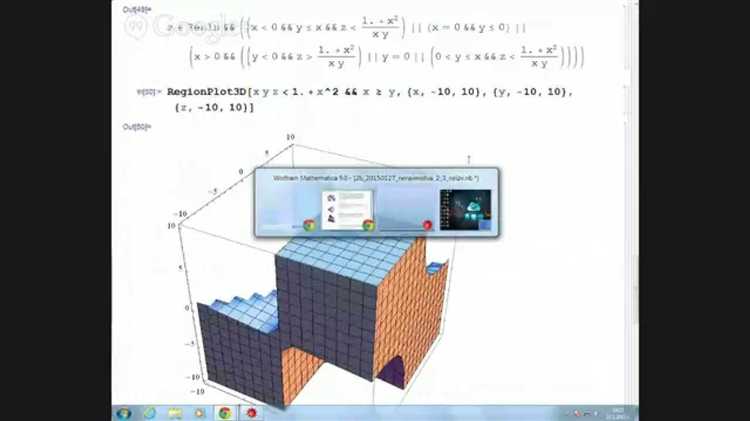
Построение графиков функций нескольких переменных с использованием Plot3D

Функция Plot3D в Mathematica применяется для визуализации скалярных функций двух переменных. Основной синтаксис: Plot3D[f[x, y], {x, xmin, xmax}, {y, ymin, ymax}]. Например, Plot3D[Sin[x y], {x, -3, 3}, {y, -3, 3}] строит поверхность функции Sin[x y] в заданной области.

Для управления качеством изображения используются параметры PlotPoints и MaxRecursion. Увеличение PlotPoints повышает плотность точек на сетке, например: Plot3D[Sin[x y], {x, -3, 3}, {y, -3, 3}, PlotPoints -> 100]. Это особенно важно для функций с быстрыми изменениями значений.

Атрибут Mesh позволяет включать или отключать сетку на поверхности. Пример: Plot3D[x^2 - y^2, {x, -2, 2}, {y, -2, 2}, Mesh -> None]. Для выделения уровней значений полезен ColorFunction, например: ColorFunction -> "Rainbow" или пользовательская функция, возвращающая цвет в зависимости от значения z.

Для повышения информативности графика применяются опции AxesLabel, PlotLabel и ImageSize. Например: AxesLabel -> {"x", "y", "f(x,y)"}, PlotLabel -> "Гиперболический параболоид", ImageSize -> Large.

Сложные формы удобно анализировать с помощью вращения 3D-графика в интерактивном режиме или с помощью команды ViewPoint, задающей фиксированный угол обзора. Пример: ViewPoint -> {2, -2, 2}.

Для ограничения области отображения по оси z применяется PlotRange, например: PlotRange -> {-1, 1}. Это полезно при наличии выбросов или резких скачков.

Если необходимо отобразить только часть поверхности, используют условную визуализацию с помощью RegionFunction. Пример: RegionFunction -> Function[{x, y, z}, x^2 + y^2 < 4] ограничит график кругом радиуса 2.

Решение дифференциальных уравнений с помощью DSolve и NDSolve

Функция DSolve используется для аналитического решения дифференциальных уравнений. Синтаксис:

DSolve[{уравнение, начальные условия}, функция, переменная]

Например, для решения уравнения y''[x] + y[x] == 0 с начальными условиями y[0] == 1, y'[0] == 0:

DSolve[{y''[x] + y[x] == 0, y[0] == 1, y'[0] == 0}, y[x], x]

Функция NDSolve предназначена для численного решения. Пример:

NDSolve[{y''[x] + y[x] == Sin[x], y[0] == 0, y'[0] == 1}, y, {x, 0, 10}]

Результат – численное представление функции y[x], пригодное для визуализации или дальнейших вычислений.

DSolve лучше использовать при простых уравнениях, когда требуется точное выражение. NDSolve подходит для сложных или систем уравнений, включая разностные и уравнения в частных производных.

Для систем уравнений указываются списки переменных и уравнений. Пример численного решения системы:

NDSolve[{
x'[t] == -x[t] + y[t],
y'[t] == -x[t] - y[t],
x[0] == 1, y[0] == 0
}, {x, y}, {t, 0, 5}]

Используйте Plot и ParametricPlot для визуализации результатов:

sol = NDSolve[{...}, {x, y}, {t, 0, 5}];
ParametricPlot[Evaluate[{x[t], y[t]} /. sol], {t, 0, 5}]

Для оценки точности численного решения применяйте параметры AccuracyGoal и PrecisionGoal. Например:

NDSolve[{...}, {y}, {x, 0, 10}, AccuracyGoal -> 8, PrecisionGoal -> 8]

Избегайте DSolve при жёстких системах и stiff-проблемах – используйте NDSolve с явным указанием метода, например Method -> "StiffnessSwitching".

Применение символьного интегрирования для вычисления определённых и неопределённых интегралов

Символьное интегрирование в Mathematica реализовано через функцию Integrate, которая позволяет получать аналитические выражения для неопределённых и определённых интегралов с высокой степенью точности. Например, вызов Integrate[Sin[x]^2, x] немедленно возвращает результат x/2 - Sin[2 x]/4, что невозможно в большинстве численно-ориентированных систем.

Для определённого интеграла используется форма Integrate[f, {x, a, b}]. При этом Mathematica учитывает особенности подынтегральной функции, такие как особенности, точки разрыва и область определения. Например, выражение Integrate[1/Sqrt[1 - x^2], {x, 0, 1}] возвращает π/2, корректно обрабатывая потенциальную особенность в конце отрезка.

Если выражение включает параметры, Mathematica автоматически выполняет символьное интегрирование с учетом предположений. Например, Integrate[E^(-a x^2), {x, -∞, ∞}] выдаёт Sqrt[π/a], но только при положительном a. В этом случае необходимо явно задать предположение: Assuming[a > 0, Integrate[E^(-a x^2), {x, -∞, ∞}]].

Сложные интегралы с параметрами рекомендуется вычислять пошагово. Пример: для Integrate[(x^2 + a)^(-3), x] полезно предварительно выполнить разложение или подстановку. Использование FunctionExpand и FullSimplify после интегрирования помогает упростить результат.

В случае, если Integrate не может дать аналитический результат, Mathematica выдаёт невычисленное выражение. Тогда целесообразно воспользоваться NIntegrate для численного результата или применить преобразования функции вручную (например, разложение в ряд).

Использование логических выражений и булевой алгебры в задачах

Mathematica предоставляет мощные средства для работы с логическими выражениями и булевой алгеброй, позволяющие эффективно решать задачи из областей цифровой логики, теории множеств и оптимизации.

Основные функции и подходы включают:

• LogicalExpand – раскрытие логических формул до дизъюнктивной нормальной формы (ДНФ). Позволяет упростить выражения и выявить внутреннюю структуру.
• Simplify и BooleanMinimize – минимизация логических функций по числу операций или литералов, что критично при проектировании цифровых схем.
• BooleanConvert – преобразование выражений в заданный формат (ДНФ, КНФ и др.), обеспечивающее удобство анализа и последующего использования.
• TruthTable (пользовательские функции или через Table) – генерация таблиц истинности для проверки корректности или поиска ошибок в логических функциях.

Рекомендации при работе с булевой алгеброй в Mathematica:

1. Используйте BooleanMinimize для снижения сложности формул, особенно при подготовке к аппаратной реализации.
2. Применяйте LogicalExpand для выявления всех возможных комбинаций, что важно при проверке условий или построении алгоритмов принятия решений.
3. Комбинируйте функции Simplify и BooleanConvert для удобства преобразований и повышения читаемости выражений.
4. Для автоматизации анализа создавайте скрипты генерации и проверки таблиц истинности, используя возможности Table и логических функций Mathematica.
5. Используйте логические операторы Mathematica (And, Or, Not, Xor) для точного построения формул без синтаксических ошибок.

Пример упрощения булевого выражения:

BooleanMinimize[(a && b) || (a && !b && c)]

Результат покажет минимальную форму, пригодную для практического применения. Такой подход ускоряет работу с большими логическими системами и уменьшает вероятность ошибок.

Работа с матрицами и линейными уравнениями через функции LinearSolve и Eigenvalues

В Mathematica функция LinearSolve предназначена для эффективного решения систем линейных уравнений вида A.x = b, где A – квадратная матрица коэффициентов, а b – вектор свободных членов.

• LinearSolve[A] возвращает функцию-решатель, которую можно применять к разным векторам b без повторного вычисления разложения матрицы.
• Рекомендуется использовать LinearSolve вместо Inverse[A].b для повышения численной устойчивости и производительности.
• Для разреженных матриц LinearSolve[SparseArray] работает быстрее и экономит память.
• Опция Method позволяет управлять алгоритмом решения (например, LU-разложение, QR-разложение или итерационные методы для больших систем).

Функция Eigenvalues вычисляет собственные значения матрицы, что важно для анализа спектра и свойств оператора.

• По умолчанию Eigenvalues[A] возвращает список всех собственных значений матрицы A.
• Для больших матриц полезно ограничить количество вычисляемых значений через второй параметр, например, Eigenvalues[A, k], где k – число наибольших по модулю собственных значений.
• Если матрица симметрична или эрмитова, стоит указать опцию Hermitian->True для ускорения вычислений и повышения точности.
• В задачах устойчивости и колебаний вычисление собственных значений позволяет определить характер решения системы.

Примеры практического применения:

1. Создание функции решения: solver = LinearSolve[A], затем solver[b] – быстрый способ решения при множестве различных векторов правой части.
2. Анализ динамики: vals = Eigenvalues[A] – получение спектра матрицы, что помогает выявить устойчивость системы.
3. Для больших и разреженных систем использовать LinearSolve[SparseArray[...]] и ограниченный набор собственных значений.

Вопрос-ответ:

Как в Mathematica решить систему нелинейных уравнений с несколькими переменными?

Для решения системы нелинейных уравнений в Mathematica используется функция Solve или NSolve. Solve подходит для получения точных аналитических решений, если они существуют, а NSolve выдаёт численные корни. Например, система из двух уравнений с двумя неизвестными может быть записана так: Solve[{x^2 + y^2 == 1, x - y == 0}, {x, y}]. Mathematica вернёт все корни, удовлетворяющие условиям. Если уравнения слишком сложные, то NSolve позволит найти приближённые значения.

Можно ли в Mathematica автоматизировать построение графиков функций с изменяющимися параметрами?

Да, для автоматизации построения графиков с переменными параметрами удобно использовать динамические конструкции, например, Manipulate. С помощью Manipulate можно создавать интерактивные визуализации, где значения параметров меняются ползунками или другими элементами управления. Это помогает быстро изучить, как изменение параметров влияет на форму графика. Например, Manipulate[Plot[a Sin[b x], {x, 0, 10}], {a, 1, 5}, {b, 1, 10}] создаст интерактивный график с двумя параметрами.

Как найти производную сложной функции в Mathematica?

Вычисление производной выполняется с помощью функции D. Для сложных выражений можно задать переменную, по которой берётся производная, а также порядок дифференцирования. Например, D[Sin[x^2 + 3 x], x] вернёт производную функции sin(x² + 3x) по x. Mathematica автоматически применит правило цепочки, упрощая результат. Если требуется частная производная функции нескольких переменных, то достаточно указать нужную переменную.

Какие инструменты есть в Mathematica для решения интегралов с параметрами?

В Mathematica предусмотрена функция Integrate для вычисления как неопределённых, так и определённых интегралов. При наличии параметров интеграл можно представить в общем виде, используя символические переменные. При этом Mathematica постарается вывести выражение, содержащее параметры. Если аналитическое решение отсутствует, тогда применяют NIntegrate для численного интегрирования. Например, Integrate[Exp[-a x^2], {x, -Infinity, Infinity}] даст ответ в зависимости от параметра a.

Как отладить программу на Mathematica, если возникает ошибка при вычислении?

Для выявления причин ошибок рекомендуется последовательно проверять части кода с помощью функции Print или Trace. Print позволяет выводить значения переменных на промежуточных этапах, что помогает понять, где происходит сбой. Trace даёт подробный отчёт о процессе вычисления, что полезно при сложных выражениях. Также стоит убедиться в правильности синтаксиса и наличии необходимых определений. Иногда помогает упрощение кода или разбивка на более мелкие блоки для изоляции ошибки.

Как в Mathematica задать и решить систему уравнений с несколькими переменными?

Для решения системы уравнений в Mathematica используют функцию Solve или NSolve. Внутри этой функции нужно указать список уравнений и список переменных, которые нужно найти. Например, если у вас есть система из двух уравнений с двумя неизвестными x и y, её можно записать так: Solve[{eq1, eq2}, {x, y}]. В ответ программа выдаст значения переменных, которые удовлетворяют системе. Solve даёт точное решение, если оно существует в аналитическом виде. Если же система слишком сложная или содержит нелинейные уравнения, можно использовать NSolve, который найдёт численные приближения решений.