При работе с геометрией в программировании задача нахождения площади треугольника встречается часто – от простых скриптов до встроенных расчетов в инженерных и графических приложениях. В Python для этого можно использовать как базовые формулы из школьного курса, так и более универсальные алгоритмы, подходящие для любых типов треугольников.
Если известны основание и высота, используется формула S = 0.5 * основание * высота. Такой подход не требует сторонних библиотек и реализуется в 1–2 строки кода. Однако при отсутствии высоты удобнее применять формулу Герона, которая требует только координат вершин или длины сторон. Это особенно полезно при работе с координатной геометрией.
В этой статье рассматриваются оба способа – по основанию и высоте, а также с помощью координат вершин. Примеры кода снабжены комментариями, которые показывают, как избежать типичных ошибок при вводе данных и выборе метода вычисления.
Расчёт площади по основанию и высоте
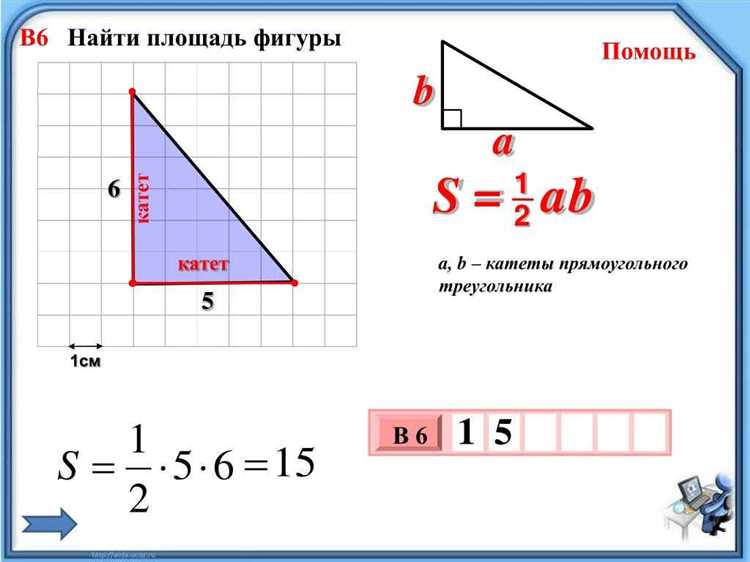
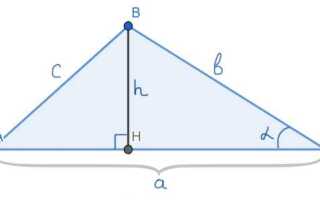
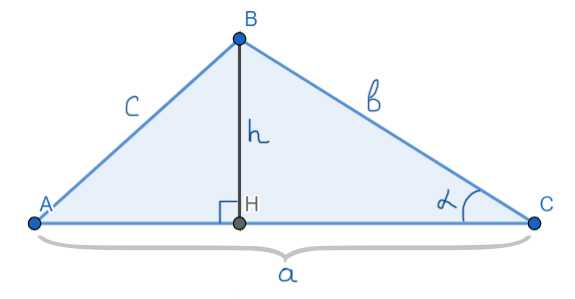
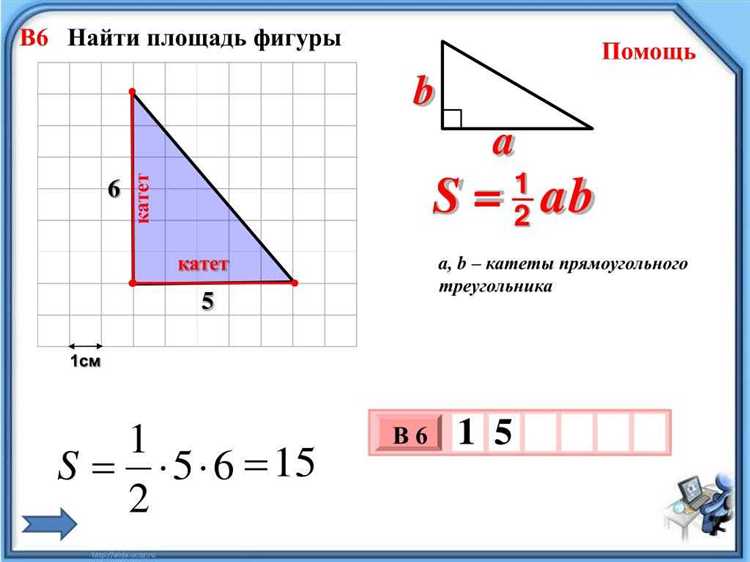
Формула: S = (a × h) / 2, где a – длина основания, h – высота, проведённая к этому основанию.
Пример кода на Python:
def triangle_area(base, height):
return (base * height) / 2
# Пример:
area = triangle_area(10, 6)
print(f"Площадь: {area}")
Типы данных base и height должны быть положительными числами. Перед расчётом проверяйте входные значения:
def triangle_area_safe(base, height):
if base <= 0 or height <= 0:
raise ValueError("Основание и высота должны быть положительными")
return (base * height) / 2
Функция возвращает число с плавающей точкой, точность зависит от переданных аргументов. Для округления используйте round():
area = round(triangle_area(10, 6), 2)Если значения получены от пользователя, применяйте float(input()) и обрабатывайте исключения:
try:
a = float(input("Введите основание: "))
h = float(input("Введите высоту: "))
print("Площадь:", triangle_area_safe(a, h))
except ValueError as e:
print("Ошибка:", e)
Использование формулы Герона с вводом трёх сторон
Для вычисления площади треугольника по формуле Герона необходимо знать длины всех трёх сторон. Формула требует предварительного вычисления полупериметра: s = (a + b + c) / 2. Затем используется выражение: S = √(s * (s — a) * (s — b) * (s — c)).
Перед вычислением следует убедиться, что стороны образуют корректный треугольник: сумма любых двух сторон должна превышать третью. Проверка: a + b > c, a + c > b, b + c > a. Без этого программа может вернуть ошибку или некорректное значение.
Пример кода на Python:
import math
a = float(input("Введите сторону a: "))
b = float(input("Введите сторону b: "))
c = float(input("Введите сторону c: "))
if a + b > c and a + c > b and b + c > a:
s = (a + b + c) / 2
area = math.sqrt(s * (s - a) * (s - b) * (s - c))
print(f"Площадь треугольника: {area}")
else:
print("Треугольник с такими сторонами не существует")Использование math.sqrt гарантирует точный результат. Ввод данных следует обрабатывать через float, чтобы избежать ошибок при делении и извлечении корня. Проверка существования треугольника обязательна для предотвращения ошибок выполнения.
Проверка существования треугольника перед вычислением
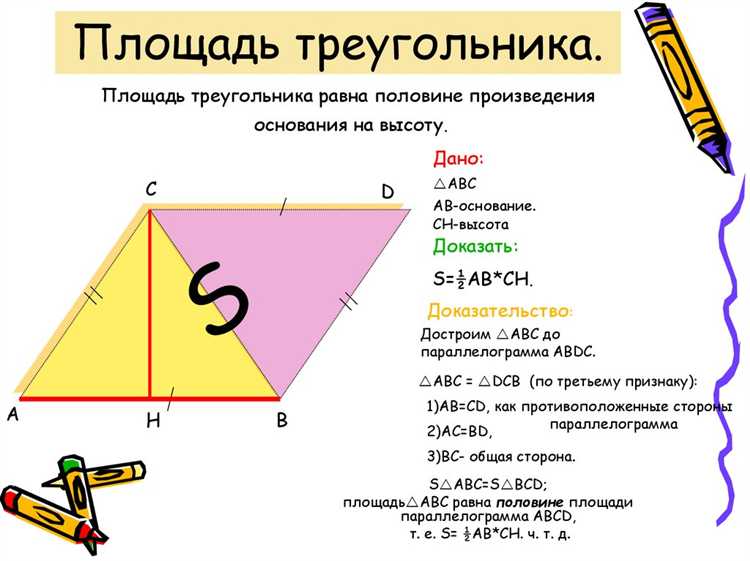
Перед вычислением площади по сторонам треугольника необходимо убедиться, что с заданными длинами сторон треугольник вообще может существовать. Это исключает бессмысленные вычисления и ошибки в работе программы.
Существует простое правило: сумма любых двух сторон треугольника должна быть больше третьей. На практике это реализуется следующим образом:
def существует_треугольник(a, b, c):
return a + b > c and a + c > b and b + c > a
Если условие не выполняется хотя бы для одной пары сторон, вычисление площади не имеет смысла – это не треугольник. Например, стороны 2, 4 и 7 не образуют треугольник, потому что 2 + 4 = 6 < 7.
Также следует учитывать граничные случаи: длины сторон должны быть положительными. Проверка на это осуществляется дополнительно:
def корректные_длины(a, b, c):
return a > 0 and b > 0 and c > 0
Рекомендуется объединить обе проверки перед основными вычислениями:
def можно_вычислить_площадь(a, b, c):
return корректные_длины(a, b, c) and существует_треугольник(a, b, c)
Только после выполнения этих условий допустимо переходить к вычислению площади по формуле Герона или другой методике.
Обработка пользовательского ввода с защитой от ошибок
Для корректного вычисления площади треугольника на основе пользовательского ввода необходимо учитывать возможные ошибки: ввод нечисловых данных, отрицательных значений и невозможных для существования треугольника комбинаций сторон.
Используйте функцию input() совместно с try-except для перехвата исключений при преобразовании строки в число. Пример:
try:
a = float(input("Введите сторону a: "))
except ValueError:
print("Ошибка: введите число.")
exit()
Аналогично обрабатывайте ввод для других сторон. После проверки формата данных убедитесь, что значения положительные:
if a <= 0:
print("Сторона должна быть положительным числом.")
exit()
Проверка условия существования треугольника обязательна. Сторона не может быть больше суммы двух других:
if a + b <= c or a + c <= b or b + c <= a:
print("Треугольник с такими сторонами не существует.")
exit()
Такой подход исключает краши при вводе текста, нулей, отрицательных чисел и невозможных комбинаций сторон. Это делает скрипт устойчивым к некорректным действиям пользователя.
Создание функции для многократного использования кода
Повторяющийся код затрудняет поддержку и увеличивает риск ошибок. Для устранения дублирования следует выделить вычисление площади треугольника в отдельную функцию.
def calculate_triangle_area(base, height):
return 0.5 * base * height
Эта функция принимает два аргумента: основание и высоту. Возвращаемое значение – числовой результат вычисления.
- Имена параметров должны быть короткими, но однозначными. Например:
base,height. - Функция не зависит от внешних данных. Это упрощает тестирование и повторное использование.
- Внутри функции не должно быть
input()иprint(), если она не предназначена для работы с пользователем.
Пример использования функции:
area = calculate_triangle_area(10, 5)
Для интеграции функции в другие модули:
- Сохраните её в отдельном файле, например,
geometry.py. - Импортируйте в основной скрипт:
from geometry import calculate_triangle_area. - Вызывайте с любыми нужными значениями, не переписывая формулу заново.
Расчёт площади по координатам вершин треугольника
Для вычисления площади треугольника по координатам его вершин можно использовать формулу, основанную на определителе матрицы. Пусть треугольник задан вершинами с координатами (x1, y1), (x2, y2), (x3, y3). Площадь S вычисляется по следующей формуле:
S = 0.5 * |x1*(y2 — y3) + x2*(y3 — y1) + x3*(y1 — y2)|
Где:
- x1, y1 – координаты первой вершины;
- x2, y2 – координаты второй вершины;
- x3, y3 – координаты третьей вершины;
- |…| – абсолютное значение результата, так как площадь не может быть отрицательной.
Пример. Пусть вершины треугольника имеют координаты: (1, 2), (3, 5), (6, 1). Подставляем эти значения в формулу:
S = 0.5 * |1*(5 — 1) + 3*(1 — 2) + 6*(2 — 5)|
После вычислений:
S = 0.5 * |1*4 + 3*(-1) + 6*(-3)| = 0.5 * |4 — 3 — 18| = 0.5 * |-17| = 0.5 * 17 = 8.5
Таким образом, площадь треугольника равна 8.5 квадратных единиц.
Этот метод позволяет точно вычислить площадь треугольника, если известны координаты его вершин. Он может быть полезен в различных задачах, связанных с геометрией и обработкой данных в программировании.
Сравнение разных способов вычислений на примерах
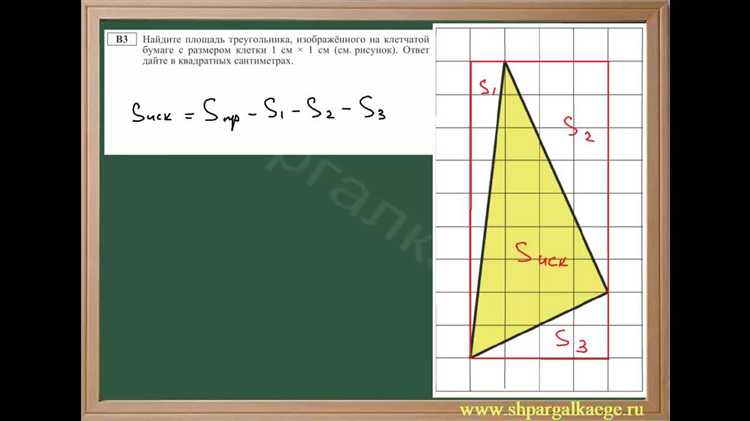
Для вычисления площади треугольника существует несколько методов, каждый из которых имеет свои особенности и ограничения. Рассмотрим несколько популярных вариантов с примерами кода на Python.
1. Формула Герона
Метод Герона используется, когда известны длины всех трёх сторон треугольника. Площадь вычисляется по формуле:
s = (a + b + c) / 2 area = (s * (s - a) * (s - b) * (s - c)) ** 0.5
Пример:
a = 3 b = 4 c = 5 s = (a + b + c) / 2 area = (s * (s - a) * (s - b) * (s - c)) ** 0.5 print(area) # 6.0
Этот метод удобен, когда все стороны известны, однако для треугольников с очень большими или маленькими сторонами могут возникнуть проблемы с точностью вычислений из-за особенностей работы с числами с плавающей точкой.
2. Формула через основание и высоту
Если известны основание и высота треугольника, площадь вычисляется по формуле:
area = (base * height) / 2
Пример:
base = 4 height = 3 area = (base * height) / 2 print(area) # 6.0
Этот метод наглядный и прост в применении, но подходит только для прямых треугольников или если высота известна. Если высоту нужно вычислить, метод теряет свою простоту.
3. Использование координат вершин треугольника
Если известны координаты трёх вершин треугольника, площадь можно вычислить с помощью формулы:
area = abs(x1*(y2 - y3) + x2*(y3 - y1) + x3*(y1 - y2)) / 2
Пример:
x1, y1 = 0, 0 x2, y2 = 4, 0 x3, y3 = 0, 3 area = abs(x1*(y2 - y3) + x2*(y3 - y1) + x3*(y1 - y2)) / 2 print(area) # 6.0
Этот метод полезен для задач, где заданы координаты, например, в графических приложениях. Однако он требует точности в вычислениях координат и может быть не столь удобен для треугольников с нестандартными углами.
4. Формула через угол между двумя сторонами
Когда известны две стороны и угол между ними, площадь вычисляется по формуле:
area = 0.5 * a * b * math.sin(angle)
Пример:
import math a = 5 b = 6 angle = math.radians(30) area = 0.5 * a * b * math.sin(angle) print(area) # 7.5
Этот способ применим, когда угол между сторонами известен, например, в геометрических и физических задачах. Однако он требует точных значений углов и может привести к ошибкам, если угол измеряется с низкой точностью.
5. Метод векторного произведения
Для треугольников в плоскости можно использовать векторное произведение. Это особенно полезно в задачах, связанных с компьютерной графикой или физикой:
area = abs((x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1)) / 2
Пример:
x1, y1 = 1, 2 x2, y2 = 4, 6 x3, y3 = 5, 1 area = abs((x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1)) / 2 print(area) # 7.5
Этот метод полезен при обработке координат, однако требует точности при вычислениях и может быть сложнее для новичков, чем другие способы.
Каждый из рассмотренных методов имеет свои преимущества и недостатки, выбор зависит от условий задачи. Например, если известны только стороны, удобен метод Герона, если треугольник задан координатами, лучше использовать формулу для площади через координаты. В задачах с углами предпочтительнее использовать метод через угол между сторонами.
Для работы с данными о треугольниках можно использовать текстовый файл, содержащий информацию о сторонах каждого треугольника. Каждый треугольник будет представлен тремя числами, соответствующими длинам его сторон. В этой задаче мы будем вычислять площади этих треугольников с использованием формулы Герона.
Пример формата данных в файле:
3 4 5 6 8 10 7 24 25
Каждая строка содержит три числа, разделенные пробелами, представляющие собой длины сторон треугольника. Необходимо выполнить следующие шаги:
- Открыть файл с данными и считать содержимое.
- Для каждой строки извлечь длины сторон треугольника.
- Вычислить площадь с помощью формулы Герона: S = √(p(p-a)(p-b)(p-c)), где p – полупериметр, а a, b, c – длины сторон.
- Вывести результат для каждого треугольника.
Пример кода для решения задачи:
import math
# Функция для вычисления площади по формуле Герона
def heron_area(a, b, c):
p = (a + b + c) / 2
return math.sqrt(p * (p - a) * (p - b) * (p - c))
# Чтение данных из файла
with open('triangles.txt', 'r') as file:
for line in file:
# Преобразование строки в числа
a, b, c = map(int, line.split())
# Вычисление площади
area = heron_area(a, b, c)
print(f"Площадь треугольника со сторонами {a}, {b}, {c} = {area:.2f}")
Этот код выполняет следующие действия:
- Читает файл построчно.
- Для каждой строки разделяет данные по пробелам и преобразует их в числа.
- Использует формулу Герона для вычисления площади.
Таким образом, можно обрабатывать данные из файла и вычислять площади треугольников, даже если количество треугольников в файле неизвестно заранее. Важно помнить, что для правильного вычисления площади треугольник должен быть допустимым (стороны должны удовлетворять неравенству треугольника).