Числа с плавающей точкой (или float) в Python представляют собой тип данных, предназначенный для хранения чисел с десятичной точкой. Однако для правильной работы с ними важно учитывать особенности их записи и точности, особенно в контексте вычислений и преобразований. В Python числа с плавающей точкой основаны на стандарте IEEE 754, что накладывает ограничения на точность и поведение таких чисел в некоторых случаях.
Запись числа с плавающей точкой в Python напрямую возможна через использование десятичной точки. Например, 3.14 или 0.001 являются корректными значениями. Однако при использовании чисел с плавающей точкой важно помнить о возможных ошибках округления и потере точности при сложных вычислениях. Например, выражение 0.1 + 0.2 не всегда будет равно 0.3 из-за особенностей внутреннего представления этих чисел.
Если точность критична, стоит обратить внимание на использование библиотеки decimal, которая позволяет работать с числами с плавающей точкой с произвольной точностью. В случае работы с финансовыми расчетами или другими сферами, где важна точность, использование этой библиотеки становится оптимальным решением. Для обычных задач можно использовать стандартный тип float, но важно осознавать его ограничения в плане точности представления чисел.
Как правильно задать число с плавающей точкой в Python

Для задания чисел с плавающей точкой в Python используется тип данных float. Чтобы создать такое число, достаточно просто указать его в виде десятичного числа с точкой. Например: 3.14, 0.1, -5.67.
Python поддерживает два основных способа задания чисел с плавающей точкой: через обычное десятичное представление и через экспоненциальное (научное) представление. Экспоненциальное представление применяется для чисел, которые слишком велики или слишком малы для обычной записи. Например, число 1.5e2 эквивалентно 150.0, а 3.2e-3 соответствует 0.0032.
Важно помнить, что при использовании чисел с плавающей точкой возможны погрешности, связанные с особенностями представления таких чисел в компьютере. Например, запись 0.1 + 0.2 не всегда будет равна точному 0.3 из-за округлений при преобразовании в двоичную форму. В таких случаях рекомендуется использовать модуль decimal, который позволяет работать с числами с фиксированной точностью, минимизируя ошибки округления.
При создании чисел с плавающей точкой важно также учитывать региональные настройки. В некоторых странах разделитель целой и дробной части числа – это запятая (например, 3,14), но в Python всегда используется точка как разделитель. Это нужно учитывать при вводе данных или работе с числовыми строками.
Для работы с точными значениями и предотвращения ошибок при вычислениях лучше избегать прямой работы с числами с плавающей точкой в критичных для точности задачах, таких как финансовые расчеты. Вместо этого используйте типы данных, обеспечивающие большую точность, или библиотеки, поддерживающие более точные вычисления.
Что такое точность чисел с плавающей точкой в Python и как её контролировать
Числа с плавающей точкой в Python представляют собой приближенные значения действительных чисел. Они хранятся в формате IEEE 754, что ограничивает точность представления и может приводить к ошибкам округления при выполнении операций с такими числами.
Основная проблема заключается в том, что не все числа можно точно представить в двоичной системе. Например, 0.1 в десятичной системе не имеет точного аналога в двоичной системе, и это приводит к погрешностям в расчетах. Эти погрешности могут накапливаться при выполнении операций с несколькими числами и вызывать отклонения от ожидаемых результатов.
Для контроля точности чисел с плавающей точкой в Python можно использовать несколько методов:
1. Ограничение точности с помощью округления. Функция round() позволяет задать количество знаков после запятой, до которых необходимо округлить число. Например, round(0.1 + 0.2, 1) вернёт 0.3. Однако, стоит помнить, что округление не устраняет погрешности, а лишь скрывает их.
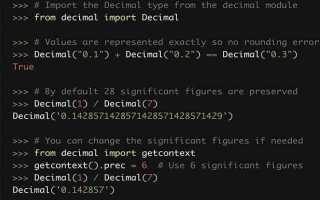
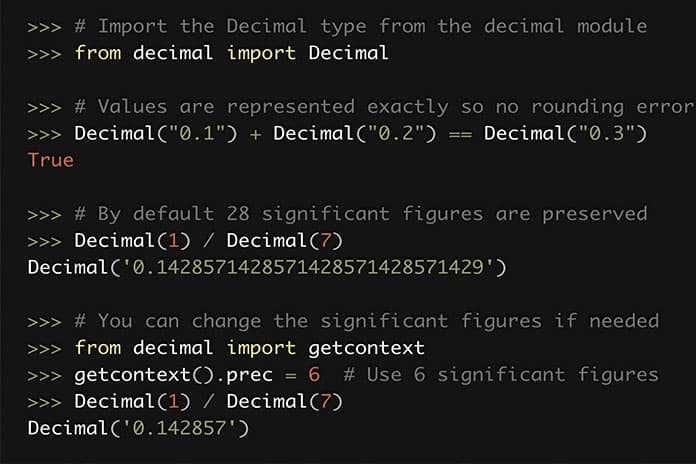
2. Использование библиотеки decimal. Модуль decimal предоставляет тип данных Decimal, который позволяет контролировать точность вычислений с произвольной точностью. Для заданной точности можно установить контекст с помощью getcontext().prec. Это позволяет избежать ошибок округления, характерных для стандартных чисел с плавающей точкой. Например, создание объекта Decimal и выполнение операций с ним может выглядеть так:
from decimal import Decimal, getcontext
getcontext().prec = 6
a = Decimal('0.1')
b = Decimal('0.2')
result = a + b
print(result) # 0.33. Использование библиотеки fractions. Когда необходимо работать с точными дробями, библиотека fractions позволяет представлять числа как дроби и выполнять операции с ними, не теряя точности. Например, fractions.Fraction(1, 3) создаст точную дробь для числа 1/3, в отличие от приближённого представления в формате float.
4. Тестирование на равенство с небольшой погрешностью. Для сравнения чисел с плавающей точкой в Python часто используют метод, основанный на проверке разницы между числами, а не на их прямом сравнении. Это можно сделать с помощью функции math.isclose(), которая позволяет задать допустимую погрешность для сравнения чисел. Пример:
import math
x = 0.1 + 0.2
y = 0.3
print(math.isclose(x, y, rel_tol=1e-9)) # TrueПри правильном контроле точности можно избежать большинства проблем, связанных с погрешностями чисел с плавающей точкой в Python. Использование decimal или fractions позволяет работать с числами с точностью, необходимой для конкретной задачи. Важно помнить, что стандартный тип данных float подходит для большинства случаев, но в ситуациях, где требуется высокая точность, лучше использовать специализированные модули.
Использование формата строки для отображения чисел с плавающей точкой
Для форматирования чисел с плавающей точкой применяются следующие основные подходы:
- Строки формата f-строки (начиная с Python 3.6) – это современный и удобный способ вставлять выражения в строки. Он позволяет задавать точность чисел с плавающей точкой напрямую.
- Метод .format() – применяется в более старых версиях Python, но все еще широко используется благодаря своей гибкости.
- Оператор % – старый способ, но тоже встречается в коде, который нужно поддерживать.
Наиболее часто для отображения чисел с плавающей точкой используется f-строка. Рассмотрим основные возможности и примеры:
число = 3.14159
число = 3.14159
В примере выше число будет выровнено по правому краю, а если оно будет короче 10 символов, то будут добавлены пробелы слева.
число = -3.14159
- Использование научной записи: для отображения чисел в экспоненциальной форме используется формат ".e".
число = 1234567.89
Когда число слишком велико или мало, Python автоматически может представить его в виде научной записи, что часто используется для работы с очень большими или очень маленькими числами.
Для старых версий Python можно использовать метод .format(), который имеет аналогичные возможности:
число = 3.14159
Метод .format() поддерживает те же самые параметры, что и f-строки, однако в некоторых случаях он менее удобен, особенно при сложных вложенных форматах.
Использование оператора % для форматирования чисел выглядит так:
число = 3.14159
Этот метод старый, но в некоторых случаях, например, при работе с кодом, который не поддерживает более новые версии Python, его всё ещё можно встретить.
Для эффективного использования формата строк в Python важно всегда помнить о следующих рекомендациях:
- Используйте f-строки (Python 3.6+) для лучшей читаемости и гибкости кода.
- Если нужно соблюдать точность, задавайте количество знаков после запятой, избегая лишних или недостаточных данных.
- Если важен знак, всегда используйте параметр "+".
- При работе с большими числами предпочтительнее использовать научную запись, чтобы сохранить читаемость данных.
- Метод .format() является хорошей альтернативой, если вы работаете с более старыми версиями Python.
Как избежать ошибок округления при вычислениях с плавающей точкой
Ошибки округления при вычислениях с числами с плавающей точкой возникают из-за того, что компьютеры не могут точно представить все действительные числа. Это приводит к потерям точности, особенно при сложных вычислениях. Чтобы минимизировать эти ошибки, можно использовать несколько эффективных методов.
1. Использование типа Decimal
Вместо стандартных типов float, которые имеют ограниченную точность, можно использовать тип Decimal из модуля decimal. Этот тип предоставляет произвольную точность и лучше подходит для финансовых и других точных расчетов. Например, для деления 1 на 3 вы получите точный результат, а не ограниченную десятичную дробь, как это происходит с float.
Пример:
from decimal import Decimal
a = Decimal(1) / Decimal(3)
print(a)
2. Округление с заданной точностью
Если точность вычислений не критична, но необходимо избегать ошибок округления, можно использовать встроенную функцию round(). Однако она не всегда идеально решает проблему, так как округление может быть неточным при очень больших или очень малых числах. Для большей надежности используйте round() в комбинации с определением количества знаков после запятой, необходимого для вашего случая.
Пример:
result = round(1.234567, 2) # округление до двух знаков после запятой
print(result)
3. Учитывание погрешности при сравнении чисел
Когда требуется сравнение чисел с плавающей точкой, следует избегать прямого сравнения с использованием оператора ==. Это связано с тем, что небольшие погрешности могут привести к неверным результатам. Вместо этого проверяйте, что разница между числами не превышает заданного порога (эпсилона).
Пример:
epsilon = 1e-9
a = 0.1 + 0.2
b = 0.3
if abs(a - b) < epsilon:
print("Числа равны с учетом погрешности")
4. Систематическое использование точных типов данных
При вычислениях, где точность критична, например, при работе с денежными суммами, используйте типы данных, предназначенные для точных представлений чисел. Decimal и fractions.Fraction обеспечат более точные результаты, чем стандартные float или double.
5. Использование внешних библиотек для точных вычислений
Если стандартные средства Python не обеспечивают нужной точности, можно использовать внешние библиотеки, такие как mpmath, которая позволяет работать с произвольной точностью. Такие библиотеки часто используются в научных расчетах и при работе с большими числами.
Пример с mpmath:
from mpmath import mp
mp.dps = 50 # задаем количество знаков после запятой
a = mp.pi
print(a)
6. Внимание к результатам промежуточных вычислений
Не забывайте о том, что промежуточные результаты также могут накапливать ошибки округления. Если возможно, выполняйте вычисления в последовательности, минимизируя потери точности на каждом шаге. Например, можно сначала умножить или сложить числа с большой точностью, а уже на последнем шаге округлить результат.
Пример:
a = 0.1
b = 0.2
c = 0.3
result = round(a + b, 1) == round(c, 1) # сначала округляем суммы, затем сравниваем
print(result)
Соблюдая эти рекомендации, вы сможете существенно снизить количество ошибок округления в своих расчетах и добиться точных результатов даже при работе с числами с плавающей точкой в Python.
Использование библиотеки decimal для работы с высокоточной арифметикой
Библиотека decimal в Python предоставляет инструменты для выполнения арифметических операций с высокой точностью. Это особенно важно в тех случаях, когда стандартные типы данных с плавающей точкой (например, float) не обеспечивают необходимой точности из-за ограничений представления чисел в двоичной системе.
Основная особенность decimal заключается в том, что она позволяет задавать точность вычислений на уровне пользователя. Это можно настроить с помощью контекста, который контролирует количество знаков после запятой, а также методы округления. Важно понимать, что decimal использует десятичную систему представления чисел, что делает её более точной при работе с денежными расчетами и другими задачами, где критична точность вычислений.
Для работы с decimal нужно сначала импортировать нужный класс и установить необходимую точность:
from decimal import Decimal, getcontext
getcontext().prec = 28 # Установка точности вычислений
После этого можно создавать числа с плавающей точкой, используя Decimal, и выполнять операции с ними. Например:
a = Decimal('1.12345678901234567890123456789')
b = Decimal('2.98765432109876543210987654321')
result = a + b
print(result)
Таким образом, результат будет вычислен с заданной точностью, что важно для точных математических вычислений.
Особое внимание стоит уделить работе с округлением. Библиотека decimal предоставляет несколько стратегий округления, включая стандартные методы, такие как округление к ближайшему чётному числу (по умолчанию), и пользовательские способы:
from decimal import ROUND_HALF_UP
result = Decimal('3.14159').quantize(Decimal('0.01'), rounding=ROUND_HALF_UP)
print(result)
Кроме того, библиотека позволяет удобно работать с очень большими или очень малыми числами, которые невозможно точно выразить с использованием стандартных типов данных. Для этого используется объект Decimal, который предоставляет более гибкие возможности, чем тип float.
В контексте финансовых приложений, где важна точность до последнего знака, decimal является обязательным инструментом. Например, вычисления налогов, начислений и других сложных финансовых операций, требуют неизменности значений и точных операций, чего не может гарантировать стандартный float.
Использование decimal гарантирует, что ошибки округления и представления чисел не будут влиять на результаты, что делает её незаменимым инструментом для разработки приложений с высокими требованиями к точности арифметики.
Как корректно сравнивать числа с плавающей точкой в Python

При сравнении чисел с плавающей точкой в Python важно учитывать особенности представления этих чисел в памяти компьютера. В отличие от целых чисел, числа с плавающей точкой могут иметь погрешности, что делает их прямое сравнение ненадежным.
Для сравнения чисел с плавающей точкой рекомендуется использовать небольшую погрешность, называемую epsilon. Этот подход подразумевает проверку того, находятся ли два числа в пределах заранее заданного диапазона погрешности, а не равны ли они точно.
Пример сравнения чисел с плавающей точкой с использованием epsilon:
import math
a = 0.1 + 0.2
b = 0.3
epsilon = 1e-9 # Допустимая погрешность
if abs(a - b) < epsilon:
print("Числа равны.")
else:
print("Числа не равны.")
В данном примере погрешность установлена на уровне 1e-9, что позволяет корректно сравнивать значения с учетом возможных ошибок округления.
Другим вариантом является использование math.isclose(), который выполняет сравнение с учетом погрешности. Эта функция позволяет задать абсолютную и относительную погрешность, что делает сравнение более гибким.
Пример использования math.isclose():
import math
a = 0.1 + 0.2
b = 0.3
if math.isclose(a, b, rel_tol=1e-9):
print("Числа равны.")
else:
print("Числа не равны.")
Этот способ особенно полезен, когда нужно учитывать как масштабы чисел, так и их точность в контексте вычислений с плавающей точкой.
Если необходимо сравнивать числа с плавающей точкой с большой точностью, следует использовать тип данных Decimal из модуля decimal, который предоставляет более точные результаты для арифметических операций и сравнений.
Как правильно округлять числа с плавающей точкой в Python

В Python для округления чисел с плавающей точкой используется встроенная функция round(). Она принимает два аргумента: число и количество знаков после запятой, до которого необходимо округлить. По умолчанию округление происходит до ближайшего целого числа.
Функция round() работает по методу округления "к ближайшему четному", также известному как банковское округление. Это означает, что если число находится точно посередине между двумя целыми числами, оно будет округлено к ближайшему четному числу. Например, round(0.5) вернет 0, а round(1.5) – 2.
Важно помнить, что round() не всегда дает ожидаемый результат при округлении до фиксированного числа знаков. Например, round(2.675, 2) возвращает 2.67, а не 2.68, что связано с внутренним представлением чисел с плавающей точкой в памяти. Для таких случаев лучше использовать модуль decimal, который обеспечивает более точное округление.
Для округления с контролем точности можно использовать функцию Decimal из модуля decimal, где доступна опция выбора метода округления. Например, Decimal('2.675').quantize(Decimal('0.01'), rounding=ROUND_HALF_UP) округлит число до 2.68, что позволяет избежать проблемы, связанной с округлением на основе четности.
Для простых случаев округления до фиксированного числа знаков после запятой вполне достаточно использования round(). Однако, если требуется высокая точность или специфические методы округления, рекомендуется обратить внимание на модуль decimal и параметры округления, такие как ROUND_HALF_UP или ROUND_HALF_DOWN.
Когда и зачем использовать тип данных float и Decimal в Python
Тип данных float и класс Decimal служат для представления чисел с плавающей точкой, но каждый из них имеет свои особенности и области применения.
float основан на стандартном формате IEEE 754 для представления чисел с плавающей точкой. Он быстро выполняется, но имеет ограниченную точность из-за особенностей двоичного представления чисел. Поэтому использование float предпочтительно в задачах, где важна производительность, а точность не критична.
Пример использования float:
- Математические расчёты, где небольшие погрешности допустимы, например, в графике или моделировании физических процессов.
- Работа с большими объёмами данных, где важно минимизировать затраты времени на вычисления.
Однако для задач, где точность чисел имеет большое значение, например, при финансовых расчётах, рекомендуется использовать Decimal. Этот класс обеспечивает произвольную точность и не зависит от двоичного представления, что исключает ошибки округления при операциях с дробными числами.
Пример использования Decimal:
- Финансовые операции, где важно сохранять точность до нескольких знаков после запятой.
- Работа с точными значениями, например, при вычислениях в научных исследованиях или при обработке измерений в инженерных задачах.
Основные отличия между float и Decimal:
float работает быстрее, но может терять точность при вычислениях с большими или дробными числами.Decimal обеспечивает точность, но требует больше вычислительных ресурсов, что делает его менее подходящим для задач, где важна производительность.Decimal лучше использовать, если необходимо соблюдать точность в финансовых и бухгалтерских приложениях, где ошибка на уровне малых чисел может привести к значительным последствиям.
Выбор между float и Decimal зависит от требований к точности и скорости вычислений в вашей программе. В большинстве случаев для общих вычислений вполне достаточен float, однако для работы с деньгами или ситуациями, где важна высокая точность, стоит использовать Decimal.
Вопрос-ответ:
Как правильно записывать числа с плавающей точкой в Python?
Числа с плавающей точкой в Python записываются как обычные числа, например, 3.14 или 2.0. Важно помнить, что Python использует тип данных float для таких чисел. Также можно использовать экспоненциальную запись, например, 1.5e2, что будет равно 150.0. Это может быть полезно при работе с очень большими или очень маленькими числами.
Почему числа с плавающей точкой могут вести себя неожиданно в Python?
Числа с плавающей точкой в Python представляют собой приближенные значения, так как они хранятся в двоичной форме. Из-за этого могут возникать проблемы с точностью при операциях с такими числами. Например, выражение 0.1 + 0.2 может не дать точный результат, а вывести 0.30000000000000004. Это связано с особенностями представления чисел с плавающей точкой в компьютерах.
Как избежать ошибок при работе с числами с плавающей точкой в Python?
Для работы с числами с плавающей точкой без потери точности в Python можно использовать модуль Decimal из стандартной библиотеки. Этот тип данных позволяет работать с числами с фиксированной точностью, избегая ошибок округления. Например, Decimal("0.1") + Decimal("0.2") даст точный результат 0.3. Это особенно важно, если нужно работать с деньгами или другими точными расчетами.
Что такое точность и погрешности при работе с числами с плавающей точкой в Python?
Точность чисел с плавающей точкой в Python ограничена внутренним представлением чисел в двоичной системе. Это может привести к небольшим погрешностям в расчетах. Например, 0.1 в двоичной системе не может быть точно представлено, что вызывает небольшие ошибки при вычислениях. Для повышения точности важно использовать модуль Decimal или округлять числа с помощью функции round().
Какие есть способы округления чисел с плавающей точкой в Python?
В Python существует несколько способов округления чисел с плавающей точкой. Один из самых распространенных методов — это использование функции round(). Например, round(3.14159, 2) вернет 3.14, округляя число до двух знаков после запятой. Также можно использовать методы, такие как math.floor() и math.ceil() для округления до ближайшего меньшего или большего целого числа соответственно. Эти методы полезны, когда нужно контролировать округление в математических расчетах.