Какие виды графических зависимостей можно построить в mathcad

Программное обеспечение Mathcad предоставляет мощные инструменты для визуализации математических зависимостей, что делает его незаменимым в инженерных и научных расчетах. Одной из ключевых возможностей является создание графиков, которые позволяют наглядно представить взаимосвязь между различными величинами. В Mathcad можно строить как простые, так и сложные графики, включая 2D и 3D визуализации, что предоставляет широкие возможности для анализа данных и принятия решений.

Существует несколько основных типов графических зависимостей, которые можно построить в Mathcad. К ним относятся графики функций, параметрические графики, а также графики данных, полученных в ходе экспериментов или расчетов. Все эти виды графиков обеспечивают эффективное представление зависимости между переменными, но выбор конкретного типа зависит от поставленной задачи. Например, для анализа изменения функции в зависимости от времени удобнее всего использовать стандартный график функций, в то время как для представления взаимосвязи двух переменных через траекторию в пространстве подходит параметрический график.

Особое внимание стоит уделить использованию многослойных графиков. Mathcad позволяет накладывать несколько графиков на один, что особенно полезно при сравнении различных зависимостей или при анализе данных, полученных в рамках одного эксперимента. Важно помнить, что правильный выбор типа графика помогает не только улучшить восприятие информации, но и избежать ошибок при интерпретации данных, особенно если речь идет о сложных инженерных расчетах.

Для эффективной работы с графиками в Mathcad важно учитывать: точность исходных данных, тип зависимостей, а также необходимость настройки осей и отображения дополнительных параметров, таких как сетка или легенда. Это позволяет сделать график более информативным и соответствующим поставленным задачам, что повышает качество анализа.

Построение графиков для анализа функций в Mathcad

Mathcad предоставляет мощные инструменты для построения графиков, которые могут помочь в визуализации зависимости между переменными и анализе функций. Построение графиков в Mathcad представляет собой не просто отображение данных, но и активное исследование математических моделей с помощью интерактивных визуализаций.

Для построения графиков в Mathcad используется встроенная функция графиков, которая позволяет наглядно представить зависимости. Один из ключевых аспектов работы с графиками – это возможность быстро менять параметры и наблюдать их влияние на функцию в реальном времени. Важным элементом является использование диапазонов значений для осей, что позволяет динамично изменять область отображения графика.

1. Создание простого графика функции

Для того чтобы построить график функции в Mathcad, необходимо определить функцию и задать диапазон значений для переменной. Например, для функции y = sin(x) с диапазоном значений от 0 до 10 можно ввести следующее:

f(x) := sin(x)
x := 0, 0.1..10

После этого для отображения графика необходимо выделить диапазон значений переменной x и функцию f(x), после чего выбрать команду для построения графика. Mathcad автоматически отобразит кривую функции на графике.

2. Множественные графики на одном экране

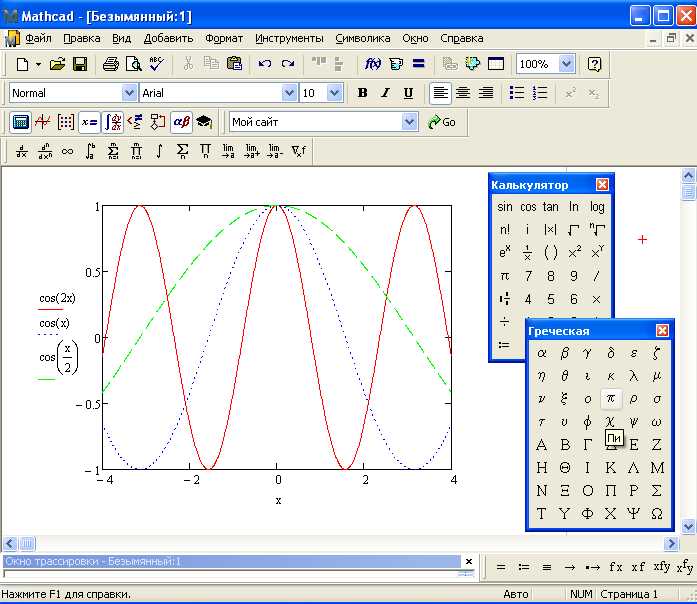
Mathcad позволяет строить несколько графиков на одном экране, что удобно для сравнения различных функций. Для этого достаточно добавить дополнительные функции в выражения и использовать разделение осей для разных графиков. Например:

g(x) := cos(x)
h(x) := tan(x)

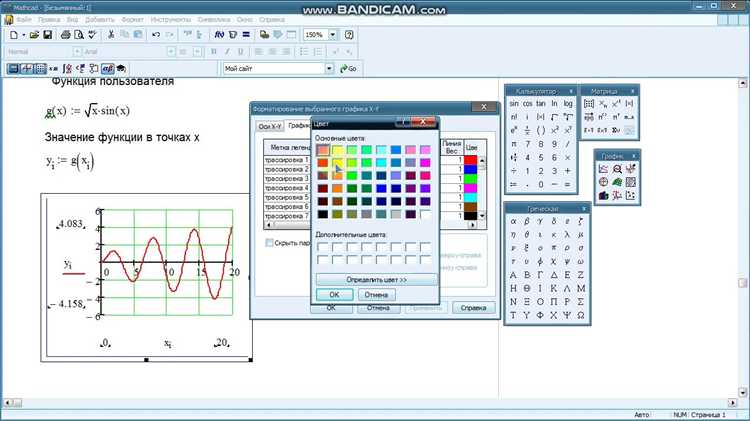
Затем на графике можно отобразить сразу f(x), g(x) и h(x) с использованием различных цветов и типов линий для каждого графика.

3. Настройка осей графика

Mathcad предоставляет гибкие настройки для осей графика. Пользователь может выбрать тип шкалы для осей (линейная или логарифмическая), а также вручную задать пределы осей. Это особенно полезно, когда необходимо исследовать поведение функции при очень больших или малых значениях переменных. Для этого в Mathcad доступны настройки масштаба осей, которые можно изменить через меню параметров графика.

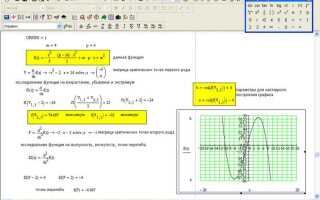
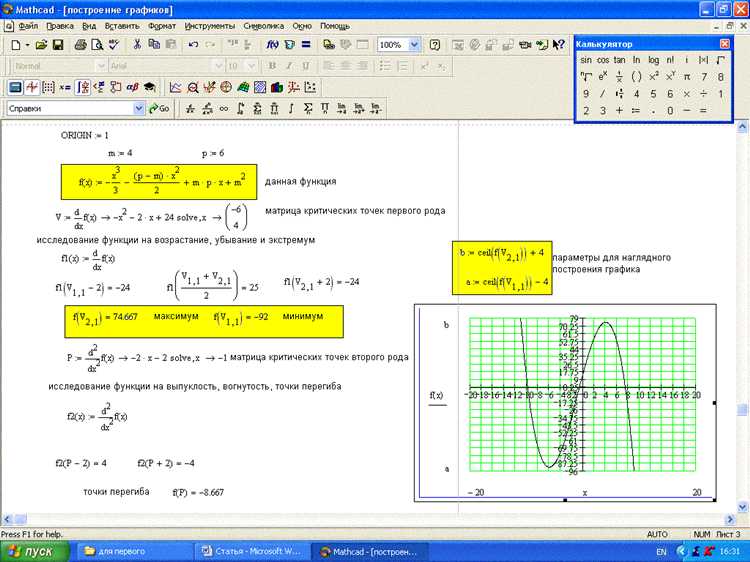
4. Анализ производных и экстремумов

Mathcad позволяет анализировать функции с помощью производных и искать экстремумы графиков. Для нахождения производной функции можно воспользоваться встроенной функцией diff(), которая позволит получить производную и построить график этой функции. Например, для функции f(x) = x^2:

f'(x) := diff(x^2, x)

После этого можно построить график как самой функции, так и её производной для дальнейшего анализа. Это особенно полезно для нахождения точек максимума и минимума функции.

5. Использование аннотаций и комментариев на графиках

Mathcad предоставляет возможность добавления аннотаций, меток и комментариев на графиках, что упрощает интерпретацию результатов. Для этого можно использовать инструменты для вставки текста и стрелок, которые помогут выделить ключевые точки на графиках, такие как максимумы, минимумы или особые точки пересечений.

6. 3D-графики для многомерного анализа

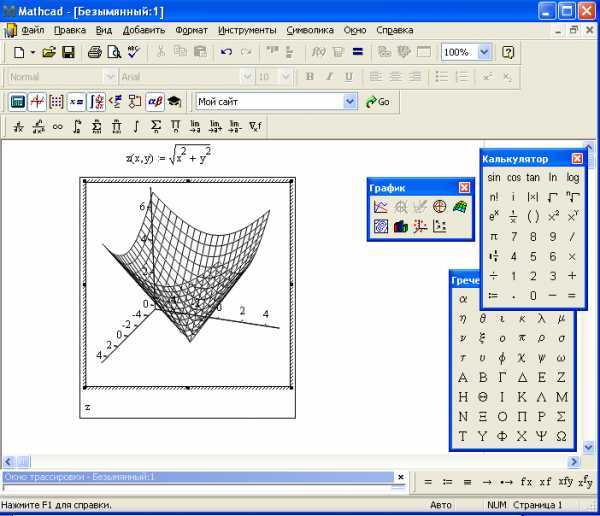
Для анализа зависимостей с несколькими переменными Mathcad позволяет строить 3D-графики. Это полезно, когда необходимо визуализировать функции двух переменных. Для построения 3D-графика достаточно задать две переменные и соответствующую функцию, а затем выбрать соответствующий тип графика. Например:

f(x, y) := x^2 + y^2
x, y := -5..5, -5..5

Такой график позволяет наглядно увидеть, как меняется функция в зависимости от двух переменных.

Гибкость Mathcad в построении графиков и анализе функций делает его мощным инструментом для математиков и инженеров, позволяя не только визуализировать зависимости, но и активно исследовать их.

Графические зависимости для решения уравнений с несколькими переменными

Графический метод решения уравнений с несколькими переменными в Mathcad позволяет наглядно представить математическую задачу и оценить её решение через визуализацию. Использование графиков помогает обнаружить закономерности и взаимосвязи, которые могут быть не очевидны при чисто аналитическом подходе.

Для уравнений с двумя переменными, например, уравнение вида f(x, y) = 0, можно построить график, который будет представлять собой кривую, показывающую все возможные комбинации значений переменных, при которых уравнение выполняется. В Mathcad для этого достаточно ввести функцию и построить её график в нужном диапазоне значений переменных. Такой график может быть двумерным или трёхмерным, в зависимости от сложности задачи.

В случае более сложных уравнений, например, с тремя или более переменными, визуализация становится более трудной, однако можно использовать проекции, которые позволяют свести многомерные задачи к двумерным. В Mathcad можно легко отображать такие зависимости с помощью диаграмм уровня или сечения многомерных поверхностей.

Для решения системы уравнений с несколькими переменными, важно точно определить области, где уравнения пересекаются. Это можно сделать с помощью отображения уровней или изо-линией на графике. При этом важно учитывать, что для решения системы необходимо строить несколько графиков, соответствующих каждому уравнению системы, и искать их пересечения.

Математическое моделирование в Mathcad позволяет более детально исследовать поведение системы в различных точках и нахождение оптимальных решений. Например, при решении задачи оптимизации с несколькими переменными, важно использовать графики, чтобы увидеть поведение целевой функции в разных областях.

Когда требуется отобразить функции с несколькими переменными в одном графике, рекомендуется использовать 3D-поверхности. Для этого в Mathcad можно строить трёхмерные графики, где одна ось будет представлять значения одной переменной, а другие оси – остальных переменных. Такой подход позволяет более чётко понять, как меняются значения функции при изменении параметров.

Кроме того, для работы с уравнениями с несколькими переменными часто используются динамические графики, которые позволяют изменять параметры и сразу видеть изменения на графике. Это особенно полезно в задачах, где требуется оптимизация или анализ чувствительности.

Использование 3D-графиков для визуализации многомерных данных

Основное преимущество 3D-графиков заключается в их способности отображать больше информации в одном изображении. Например, если для двух переменных можно построить стандартную плоскостную диаграмму, то для трёх – используется трёхмерная поверхность, где оси X, Y и Z представляют различные параметры. Это позволяет проанализировать зависимости не только по двум осям, но и по третьей, которая может быть зависимой переменной.

Пример: для изучения зависимости температуры (Z) от времени (X) и влажности (Y) можно использовать 3D-график, на котором будет видно, как изменение влажности влияет на температуру в зависимости от времени. Такой подход помогает учесть несколько факторов одновременно, предоставляя более полное представление о динамике процесса.

Создание 3D-графика в Mathcad требует аккуратности при выборе данных и настройки визуализации. Важно правильно выбрать диапазоны значений для осей и их масштабы, чтобы не терять важных деталей. Например, если одна из осей будет слишком сжата, это может привести к неправильной интерпретации данных.

Для эффективной работы с 3D-графиками в Mathcad можно использовать инструмент «3D график», где автоматически строится поверхность, отражающая заданные зависимости. В интерфейсе можно настраивать угол обзора, освещение, а также выбрать тип графика (поверхность, контуры или объём). Чтобы визуализировать более сложные зависимости, можно использовать разные виды поверхностей и настройку цвета, что делает график более информативным и легко воспринимаемым.

Кроме того, важным аспектом является возможность анимации 3D-графиков в Mathcad. Это позволяет наблюдать за изменениями данных в реальном времени, что особенно полезно в динамических моделях или для данных с временными компонентами.

В итоге, 3D-графики Mathcad – это незаменимый инструмент для аналитиков и исследователей, работающих с многомерными данными. Они дают возможность детально изучать сложные зависимости и улучшать процесс принятия решений на основе визуализированных данных.

Интерактивные графики: настройка параметров и взаимодействие с данными

Интерактивные графики в Mathcad предоставляют мощные возможности для анализа данных в реальном времени, позволяя пользователю настраивать параметры графика и наблюдать за изменениями визуализации. В этой статье рассмотрим, как правильно настроить параметры интерактивных графиков и использовать их для более глубокого взаимодействия с данными.

Основным элементом интерактивных графиков является использование параметров, которые могут изменяться пользователем. Для этого в Mathcad применяются управляющие элементы, такие как слайдеры, кнопки или поля ввода. Настройка таких элементов осуществляется через интерфейс Mathcad с помощью соответствующих функций и операторов. Например, с помощью слайдера можно изменять значения параметра, который влияет на форму графика, что позволяет наблюдать за результатами в реальном времени.

Для создания интерактивных графиков, необходимо сначала определить переменные, которые будут изменяться, и установить диапазоны их значений. Затем, используя функцию «Контроллеры» (например, слайдеры), можно настроить диапазоны изменения этих переменных. Каждый параметр в Mathcad можно привязать к графическому объекту, чтобы при изменении значения параметра происходили динамические изменения на графике.

Важным моментом является использование функций для обработки данных в зависимости от изменения параметров. Например, если на графике отображаются функции, которые зависят от переменных, то при изменении этих переменных график будет автоматически пересчитываться, и пользователю предоставится актуальная информация. Это позволяет быстро и эффективно анализировать влияние различных факторов на данные без необходимости вручную перерисовывать графики.

Кроме того, Mathcad поддерживает возможность взаимодействия с несколькими графиками одновременно. Это особенно полезно, когда требуется проанализировать, как изменения одного параметра на одном графике влияют на результаты других графиков. Например, можно создать график зависимости температуры от времени и одновременно отобразить зависимость давления от температуры, используя взаимосвязанные параметры.

Для повышения удобства работы с интерактивными графиками, Mathcad позволяет интегрировать визуальные элементы в отчет или презентацию. В этом случае, пользователь может не только управлять параметрами, но и демонстрировать изменения в графиках для наглядного представления данных. Это особенно важно при проведении научных исследований или инженерных расчетов, где визуализация имеет ключевое значение для анализа данных и принятия решений.

При настройке интерактивных графиков также важно учитывать производительность программы. Большие объемы данных или сложные вычисления могут привести к замедлению работы графиков. В таких случаях рекомендуется оптимизировать использование переменных и функций, а также по возможности ограничить количество отображаемых точек данных, чтобы ускорить обновление графиков.

Методы отображения производных и интегралов в графическом виде

В Mathcad для отображения производных и интегралов используются различные методы, которые позволяют эффективно визуализировать зависимости и анализировать поведение функций. Рассмотрим основные подходы, доступные в этом программном обеспечении.

Отображение производных

Производную функции можно представить графически двумя основными способами:

График производной функции: Путь отображения производной заключается в построении графика функции её производной. Это позволяет наглядно увидеть изменение наклона функции в каждой точке. Для этого в Mathcad достаточно использовать операторы дифференцирования, например, d(f(x), x), где f(x) – исходная функция, а x – переменная.
Тангенциальная линия: Отображение производной в виде касательной линии позволяет увидеть моментальное изменение функции в определенной точке. Для этого нужно построить график функции и затем отобразить касательную, вычисленную в выбранной точке. В Mathcad можно использовать команды tangent(f(x), x0), где x0 – точка, в которой строится касательная.

Этот метод особенно полезен при изучении функции на больших интервалах, поскольку позволяет увидеть не только значение производной в точке, но и её поведение на графике.

Отображение интегралов

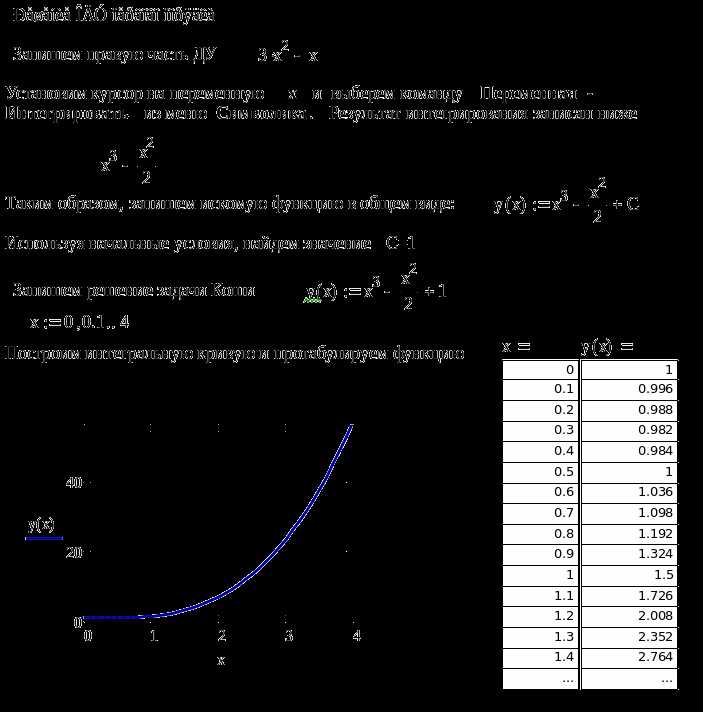
Для интегралов в Mathcad также предусмотрены несколько методов визуализации:

График функции и площади под ней: Графическое отображение интеграла в виде площади, заключенной между графиком функции и осью абсцисс, позволяет наглядно продемонстрировать значение определенного интеграла. Для этого нужно построить график функции и затем выделить нужную область. В Mathcad это реализуется через команду integral(f(x), a, b), где a и b – границы интегрирования.
Построение графика неопределенного интеграла: График неопределенного интеграла можно построить с помощью операции integral(f(x), x). Этот метод позволяет наглядно увидеть зависимость между функцией и её первообразной. Результатом будет кривая, которая отображает все возможные значения неопределенного интеграла.

Важно отметить, что в Mathcad можно добавить различные аннотации для выделения области, соответствующей интегралу, а также использовать цветовые маркеры для выделения значимых частей графика.

Построение графиков для анализа экспериментальных данных и их интерполяция

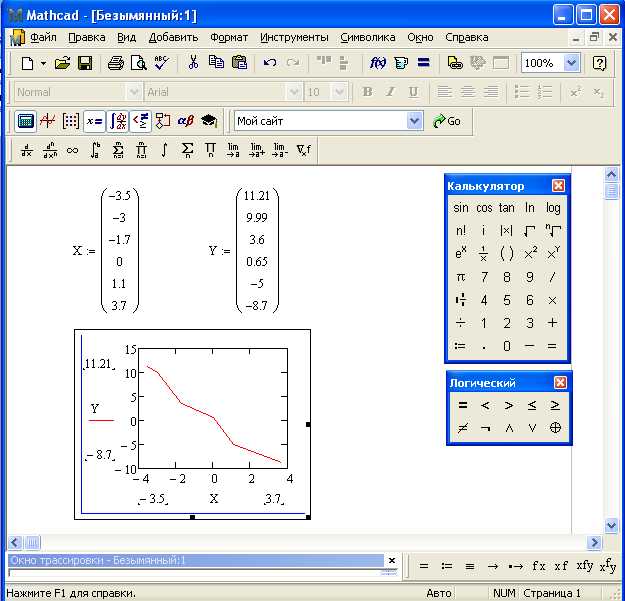
Для построения графика на основе экспериментальных данных в Mathcad достаточно просто задать два вектора значений: один для независимой переменной (например, времени или температуры), второй – для зависимой (например, измеренной величины). Это позволяет мгновенно получить точечный график, который будет показывать, как данные изменяются в зависимости от выбранной переменной.

После создания точечного графика следующим шагом является интерполяция. Интерполяция данных позволяет создать плавную кривую, которая будет приблизительно описывать тенденции, присущие экспериментальным данным. Mathcad предлагает несколько методов интерполяции: линейная, полиномиальная и сплайновая. Каждый из них подходит для различных типов данных и задач. Линейная интерполяция хорошо работает при малых изменениях данных, где предполагается линейная зависимость, а полиномиальная или сплайновая интерполяция предпочтительна, когда данные изменяются более сложным образом.

Линейная интерполяция используется, когда изменения между двумя соседними точками данных достаточно малы и можно с достаточной точностью аппроксимировать их прямой линией. Этот метод прост в применении и вычислительно не требует значительных затрат, однако он может неадекватно отображать поведение данных, если изменения между точками существенны.

Полиномиальная интерполяция применима, когда данные имеют более сложную зависимость. Для этого используется многочлен, который проходит через все точки. Однако полиномиальная интерполяция может привести к осцилляциям между точками, особенно при большом числе данных. В таких случаях рекомендуется ограничивать степень полинома, чтобы избежать переобучения модели.

Сплайновая интерполяция предлагает наиболее гладкие кривые, что делает ее подходящей для большинства экспериментальных данных. Сплайны обеспечивают плавность и непрерывность первой и второй производной, что делает результат визуально привлекательным и математически корректным. Сплайновая интерполяция особенно полезна, когда требуется сгладить резкие изменения в данных, например, в случае измерений, подверженных шуму.

Для анализа графиков в Mathcad важно использовать возможности настройки визуальных элементов. Помимо выбора типа интерполяции, можно изменять цвет и форму точек, а также линии, что поможет выделить определенные участки графика, упростить восприятие данных и подчеркнуть ключевые моменты. Важно, чтобы графики не были перегружены избыточной информацией, что могло бы затруднить их анализ.

Применение графиков для представления статистических зависимостей в Mathcad

Mathcad предоставляет мощные инструменты для визуализации статистических зависимостей с помощью графиков, что позволяет аналитикам и инженерам наглядно интерпретировать данные. Использование графиков помогает выделить закономерности, скрытые за числовыми значениями, и облегчает принятие решений на основе данных.

Основные типы графиков, используемых для статистических зависимостей:

Гистограммы – позволяют визуализировать распределение данных, показывая частоту различных значений. В Mathcad гистограммы строятся через функцию «histogram» и часто используются для анализа выборок и оценки их характеристик, таких как среднее, медиана, мода.
Диаграммы рассеяния (scatter plots) – применяются для оценки взаимосвязи между двумя переменными. В Mathcad их можно построить с использованием функции «plot». Эти графики помогают определить корреляцию и анализировать отклонения от трендов.
Линейные графики – используемые для отображения трендов во времени или зависимости между двумя величинами. Часто применяются для анализа временных рядов, например, динамики изменения финансовых показателей или температуры в течение года.

Особенности работы с графиками в Mathcad:

Настройки осей – в Mathcad можно настраивать диапазоны осей и форматирование меток, что позволяет создавать графики с четким и понятным отображением данных. Для статистических зависимостей важно корректно отображать минимальные и максимальные значения, чтобы избежать искажений.
Регрессия – Mathcad поддерживает построение линии регрессии для выявления зависимости между переменными. Включение линии тренда помогает лучше понять, какой функциональной зависимостью можно аппроксимировать данные. При этом Mathcad может автоматически вычислять параметры регрессии, такие как коэффициенты, ошибки и значимость.
Цветовое кодирование – для улучшения восприятия графиков можно использовать разные цвета для различных серий данных, что облегчает анализ мульти-данных и сравнений.

Наиболее эффективные методы применения графиков в Mathcad для статистического анализа:

Анализ корреляции – построение диаграммы рассеяния для оценки взаимосвязи между двумя переменными. В случае сильной линейной зависимости регрессионная линия будет точно отражать эту зависимость.
Проверка нормальности распределения – гистограммы и Q-Q графики помогут определить, насколько данные соответствуют нормальному распределению. Это важно для выбора корректных методов статистического анализа.
Оценка устойчивости данных – графики, показывающие изменения данных в зависимости от времени, позволяют проанализировать стабильность и выявить возможные тренды или цикличность.

Пример: анализ взаимосвязи между температурой и энергопотреблением

Для построения диаграммы рассеяния в Mathcad нужно ввести данные температуры и энергопотребления, а затем с помощью функции «scatter plot» отобразить их на графике. Построенная линия регрессии покажет зависимость между этими двумя величинами и даст возможность оценить, как изменение температуры влияет на энергопотребление.

Использование таких графиков значительно повышает эффективность статистического анализа, улучшая восприятие и интерпретацию данных, что особенно важно при принятии решений в условиях неопределенности.

Вопрос-ответ:

Какие существуют виды графических зависимостей в Mathcad?

В Mathcad можно выделить несколько типов графических зависимостей: линейные, нелинейные, экспоненциальные, тригонометрические и многие другие. Каждый тип используется в зависимости от типа задачи и формы представления данных. Линейные зависимости могут быть использованы для отображения простых соотношений, например, для анализа прямолинейных зависимостей между величинами. Нелинейные графики чаще всего используются для моделирования сложных процессов, например, в физике или инженерных расчетах. Экспоненциальные и тригонометрические зависимости, в свою очередь, отображают более сложные, но распространенные в науке и технике закономерности, такие как рост или колебания.

Как в Mathcad строится график зависимости между переменными?

Для построения графика зависимости в Mathcad нужно сначала ввести математическое выражение для функции, затем указать диапазон значений переменной. Далее в программе можно выбрать команду для построения графика, который автоматически отобразится в окне рабочего пространства. В Mathcad есть возможность изменять тип графика, добавлять сетку, оси и метки. Для анализа различных зависимостей также предусмотрены инструменты для изменения масштаба графика и добавления различных элементов, что позволяет адаптировать графическое представление под нужды пользователя.

В чем отличие линейных и нелинейных графиков зависимостей в Mathcad?

Линейные графики в Mathcad отображают зависимости, которые следуют прямой линии, что характерно для постоянных или пропорциональных соотношений между переменными. Такие графики проще анализировать и они хорошо подходят для задач с простыми математическими зависимостями. Нелинейные графики, в свою очередь, отображают более сложные зависимости, такие как квадратичные, экспоненциальные или логарифмические, где изменения в одной переменной приводят к более сложным изменениям в другой. Нелинейные зависимости часто используются в моделировании естественных процессов, таких как рост населения или изменение температуры в зависимости от времени.

Можно ли в Mathcad создавать несколько графиков для сравнения различных зависимостей?

Да, в Mathcad можно создавать несколько графиков на одном рабочем пространстве для сравнения различных зависимостей. Для этого достаточно использовать функцию «Множественный график», где можно добавить несколько выражений или функций, которые будут отображаться на одной или нескольких осях. Это позволяет наглядно сравнивать изменения различных переменных, например, для анализа их взаимосвязи или для сопоставления различных моделей. Также можно настроить легенду, цвет и стиль линий, чтобы графики были более читаемыми и понятными.