Система компьютерной алгебры Maple предоставляет широкий набор инструментов для аналитического и численного решения дифференциальных уравнений. Основная команда для работы – dsolve, которая поддерживает как обыкновенные, так и дифференциальные уравнения в частных производных. Формат записи: dsolve(уравнение, переменная) или dsolve({уравнение, начальные условия}, переменная).
Для точного управления видом решения используется параметр numeric, позволяющий получать численные приближённые решения с помощью встроенного метода Рунге-Кутты 4-го порядка. В этом режиме результатом будет процедура, которую можно вызывать для получения значения функции в конкретной точке: sol(1.5).
При работе с системами дифференциальных уравнений переменные указываются в виде списка. Например, dsolve({уравнение1, уравнение2, начальные условия}, {y(t), z(t)}, numeric). Для построения графика траектории используется команда plots[odeplot].
Если уравнение не поддаётся аналитическому решению, Maple возвращает выражение с пометкой unable to find explicit solution. В таких случаях рекомендуется либо перейти к численному методу, либо попробовать преобразовать уравнение с помощью simplify или convert.
Для дифференциальных уравнений в частных производных применяется команда pdsolve, синтаксис которой аналогичен dsolve. Однако аналитические решения PDE доступны лишь для ограниченного класса уравнений, поэтому чаще используются численные методы, включая пакет PDETools.
Задание начальных условий при решении ОДУ через dsolve
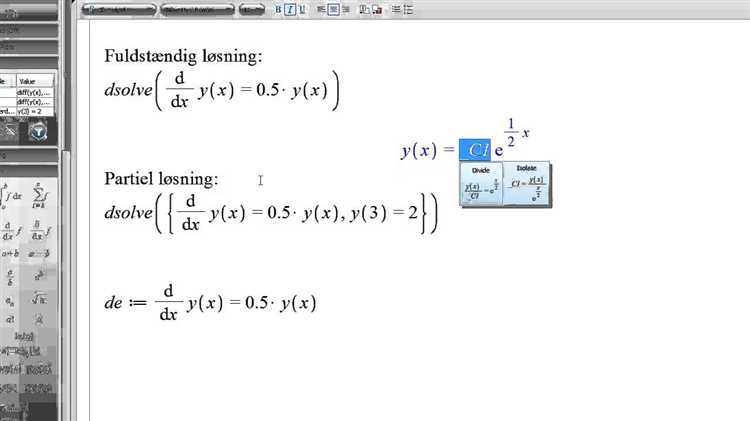
Для задания начальных условий в Maple используется аргумент initial conditions внутри вызова dsolve. Уравнение и условия передаются в виде системы.
- Синтаксис:
dsolve({уравнение, начальные условия}, функция) - Начальные условия указываются явно, например:
y(0)=1,D(y)(0)=2
Пример:
ode := diff(y(x), x, x) + 3*diff(y(x), x) + 2*y(x) = 0;
ics := y(0) = 5, D(y)(0) = -1;
sol := dsolve({ode, ics}, y(x));Если используются производные выше первого порядка, необходимо явно указывать их через D:
D(y)(0)– первая производнаяD@@2(y)(0)– вторая производная
Для систем уравнений начальные условия задаются по аналогии, включая условия для всех функций:
ode1 := diff(x(t), t) = y(t);
ode2 := diff(y(t), t) = -x(t);
ics := x(0) = 1, y(0) = 0;
sol := dsolve({ode1, ode2, ics}, {x(t), y(t)});Если требуется получить численное решение, начальные условия обязательно должны быть заданы. Используется параметр numeric:
dsolve({ode, ics}, y(x), numeric);Для передачи условий в функциональном виде удобно использовать списки:
ics := [y(0) = 2, D(y)(0) = 0];
dsolve([ode, op(ics)], y(x));Нельзя задавать противоречивые или неполные условия – Maple выдаст ошибку или вернёт неопределённый ответ.
Использование команды dsolve для получения аналитического решения
Команда dsolve в Maple применяется для нахождения аналитических решений дифференциальных уравнений. Синтаксис:
dsolve(уравнение, переменная)
Для решения обычного дифференциального уравнения первого порядка:
dsolve(diff(y(x), x) = y(x) + x, y(x))
Результат:
y(x) = -x - 1 + _C1·exp(x)
Для задания начальных условий:
dsolve({diff(y(x), x) = y(x) + x, y(0) = 1}, y(x))
Результат:
y(x) = -x - 1 + 2·exp(x)
При работе с системами уравнений:
dsolve({diff(x(t), t) = y(t), diff(y(t), t) = -x(t)}, {x(t), y(t)})
Maple возвращает общее решение с параметрами _C1, _C2.
Для получения решения в виде выражения без параметров интегрирования, требуется задать начальные условия. Например:
dsolve({diff(x(t), t) = y(t), diff(y(t), t) = -x(t), x(0) = 1, y(0) = 0}, {x(t), y(t)})
Результат:
x(t) = cos(t), y(t) = -sin(t)
dsolve(..., output = list) – список уравнений,
dsolve(..., output = operator) – функциональное представление.
Для явного получения решения в виде функции:
sol := dsolve(..., y(x));
evalf(subs(x = 2, rhs(sol)))
При невозможности аналитического решения Maple возвращает уравнение с флагом unable. В этом случае переходят к dsolve(..., numeric).
Численное решение ОДУ с использованием параметра numeric
Для численного решения обыкновенных дифференциальных уравнений в Maple применяется параметр numeric в команде dsolve. Этот параметр указывает системе использовать численные методы интегрирования, такие как метод Рунге-Кутты или адаптивные методы, реализованные во встроенном решателе.
Пример: пусть задано уравнение diff(y(x), x) = -2*y(x) + exp(-x) с начальным условием y(0) = 1. В Maple решение записывается следующим образом:
sol := dsolve({diff(y(x), x) = -2*y(x) + exp(-x), y(0) = 1}, y(x), numeric);
Для получения значения решения в точке используется вызов функции-объекта:
sol(1.0);
Результат содержит численные значения x и y(x) в указанной точке. Для построения графика применяется команда plots[odeplot]:
plots[odeplot](sol, [x, y(x)], 0 .. 5);
Для изменения метода решения используется параметр method=... внутри вызова dsolve. Например, для использования метода Эйлера: method = rkf45 или method = euler.
Контроль точности производится через параметры abserr и relerr. Пример с заданием относительной и абсолютной погрешности:
dsolve(..., numeric, abserr = 1e-6, relerr = 1e-6);
Если требуется решение системы ОДУ, уравнения и начальные условия указываются в виде множества. Например:
sys := {diff(x(t), t) = x(t) - y(t), diff(y(t), t) = x(t) + y(t), x(0) = 1, y(0) = 0};
sol := dsolve(sys, {x(t), y(t)}, numeric);
После этого sol(t) возвращает значения x(t) и y(t) в численной форме.
Построение графика решения ОДУ по численным данным
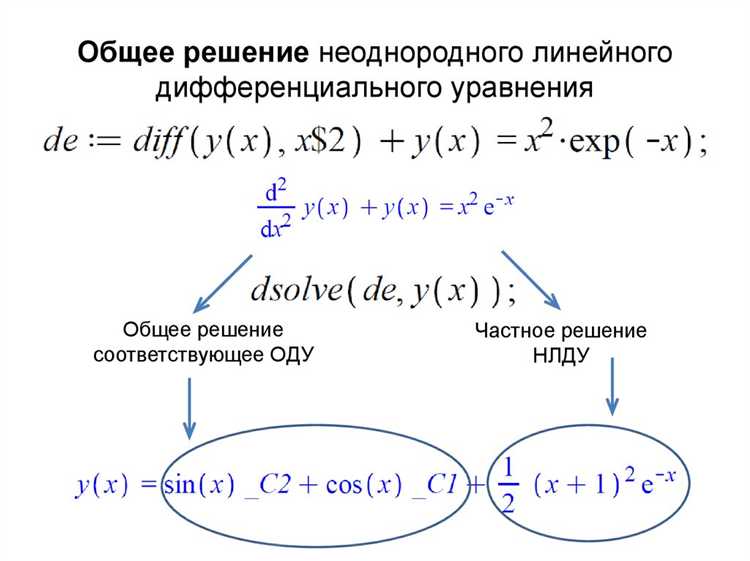
- Задается уравнение, начальные условия и интервал интегрирования:
de := diff(y(x), x) = -2*y(x) + sin(x): ic := y(0) = 1: sol := dsolve({de, ic}, y(x), numeric, output = listprocedure): - Вызывается
odeplot:with(plots): odeplot(sol, [x, y(x)], 0 .. 10);
Если требуется построить график нескольких компонент (например, векторной функции), указывается список переменных:
sys := {diff(x(t), t) = y(t), diff(y(t), t) = -x(t)}:
ics := {x(0) = 1, y(0) = 0}:
sol := dsolve(sys union ics, {x(t), y(t)}, numeric, output = listprocedure):
odeplot(sol, [x(t), y(t)], 0 .. 10);
- Для увеличения плотности точек – параметр
numpoints=N: - Для построения решения по заданному списку значений –
output = arrayиplots[pointplot]:
sol := dsolve({de, ic}, y(x), numeric, output = array([seq(i/10, i = 0 .. 100)])):
plots[pointplot]([seq([i/10, rhs(sol[i+1][2])], i = 0 .. 100)], connect=true);
При анализе жестких систем рекомендуется использовать метод Розенброка:
dsolve({de, ic}, y(x), numeric, method=rosenbrock);
Для настройки вида графика:
color– цвет линииthickness– толщинаtitle,labels,legend– аннотации
Пример:
odeplot(sol, [x, y(x)], 0 .. 10, color=red, thickness=2, title="Численное решение", labels=["x", "y"]);
Решение систем дифференциальных уравнений в Maple

Для решения систем обыкновенных дифференциальных уравнений в Maple используется команда dsolve с аргументом-списком уравнений и переменных. Формат вызова: dsolve({уравнения}, {неизвестные функции}).
Пример: система уравнений diff(x(t), t) = x(t) + y(t), diff(y(t), t) = x(t) - y(t). Команда будет выглядеть так:
sys := {diff(x(t), t) = x(t) + y(t), diff(y(t), t) = x(t) - y(t)}:
dsolve(sys, {x(t), y(t)});
Для получения численного решения добавляется параметр numeric:
dsolve(sys union {x(0) = 1, y(0) = 0}, numeric);
Результатом является процедура, которую можно вызывать, передавая значение аргумента t. Например: sol := dsolve(...); sol(1.5);
Для визуализации траектории используется odeplot из пакета plots:
with(plots):
odeplot(sol, [x(t), y(t)], t = 0..5);
Если система жёсткая, можно задать метод решения явно, например method = rosenbrock. Для получения списка доступных методов: dsolve,help.
Системы с параметрами удобно решать с помощью parameters. Например:
sys := {diff(x(t), t) = a*x(t) + b*y(t), diff(y(t), t) = c*x(t) + d*y(t)}:
dsolve(sys, {x(t), y(t)}, parameters = [a, b, c, d]);
Для уравнений с задержкой или уравнений в частных производных необходимо использовать специализированные функции, например dsolve/numeric/delay или pdsolve.
Применение условий приращения для моделирования задач Коши
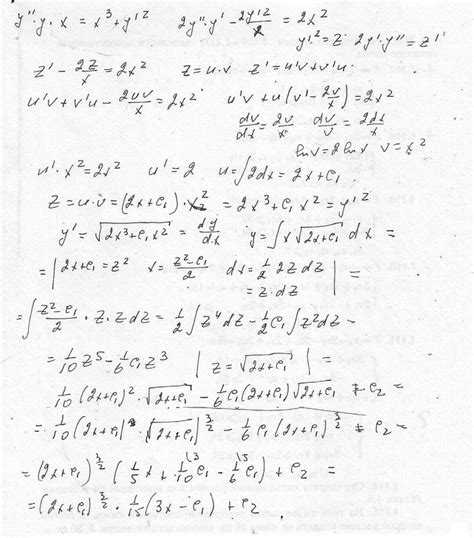
Условия приращения в Maple позволяют точно задать поведение решений дифференциальных уравнений в окрестности начальной точки, что важно при решении задач Коши. Вместо стандартных начальных условий можно использовать разностные выражения, задавая изменение функции или её производных на малом интервале.
Для моделирования задачи Коши с условиями приращения в Maple применяется команда dsolve с опцией initcond, где приращение указывается как разница значений функции в соседних точках. Например, если известен шаг h и приращение Δy, можно задать условие y(h)-y(0)=Δy. Это удобно при численном моделировании, когда данные измерений или физические параметры определяют изменение величины за фиксированный интервал.
При использовании условий приращения следует учитывать масштаб шага и точность вычислений. Слишком большой шаг может исказить модель, а слишком малый – привести к потере устойчивости. Рекомендуется выполнять предварительный анализ чувствительности решения к величине шага и сравнивать результаты с классическими начальными условиями.
Практическая рекомендация – для постановки задачи Коши с условиями приращения использовать параметризацию приращений через функции Maple, что позволяет гибко менять начальные данные без пересчёта всей модели. Это особенно актуально при исследовании динамических систем и механических колебаний, где приращения отражают реальные изменения состояния.
Использование условий приращения повышает точность и адаптивность моделирования, особенно в задачах, где невозможно задать значения функции напрямую, а известны только изменения за малые промежутки времени или пространства.
Вопрос-ответ:
Как в Maple решить обычное дифференциальное уравнение первого порядка?
Для решения уравнения первого порядка в Maple используется команда dsolve. Нужно задать уравнение в виде, например, diff(y(x), x) = f(x, y(x)), а затем вызвать dsolve с этим уравнением. Maple попробует найти общее решение, а при необходимости можно добавить начальные условия. Если уравнение решается аналитически, Maple вернёт формулу решения.
Можно ли в Maple решать системы дифференциальных уравнений? Как это сделать?
Да, Maple позволяет решать системы дифференциальных уравнений. Для этого нужно записать все уравнения системы как список или набор уравнений, например, [diff(x(t), t) = f1(t, x(t), y(t)), diff(y(t), t) = f2(t, x(t), y(t))], и передать этот список функции dsolve. При необходимости можно указать начальные условия для всех переменных. Maple вернёт решение системы в виде функций переменных от независимой переменной.
Как в Maple получить численное решение дифференциального уравнения, если аналитическое найти не удаётся?
Если аналитическое решение невозможно, dsolve в Maple позволяет получить численное приближение. Для этого нужно добавить опцию numeric к функции dsolve, например, dsolve(уравнение, numeric). При этом можно указать начальные условия, необходимые для численного метода. Maple использует встроенные численные алгоритмы, которые позволяют получить значения решения в заданном интервале с определённой точностью.
Какие типы дифференциальных уравнений Maple умеет решать автоматически?
Maple справляется с большим спектром дифференциальных уравнений: линейные уравнения с постоянными или переменными коэффициентами, уравнения с разделяющимися переменными, однородные и некоторые нелинейные уравнения, системы линейных уравнений, а также уравнения с начальными и граничными условиями. Однако есть классы уравнений, для которых аналитическое решение может отсутствовать, и тогда Maple предложит численные методы.
Как задать начальные условия для дифференциального уравнения в Maple?
Начальные условия задаются как дополнительные уравнения, в которых переменная и её производные принимают конкретные значения в некоторой точке. Например, для y(x) с условием y(0) = 1 и y'(0) = 0, нужно передать в dsolve список уравнений: [diff(y(x), x) = уравнение, y(0) = 1, D(y)(0) = 0]. Maple учтёт эти условия при поиске конкретного решения.
Как в Maple решить дифференциальное уравнение первого порядка с начальным условием?
Для решения такого уравнения в Maple используется команда `dsolve`. Если уравнение задано, например, как \(\frac{dy}{dx} = f(x,y)\), а начальное условие — \(y(x_0) = y_0\), то синтаксис будет примерно таким: `dsolve({diff(y(x), x) = f(x,y(x)), y(x0) = y0}, y(x))`. Maple автоматически найдет решение с учетом начального условия. Если уравнение аналитически решается сложно, Maple может выдать численное решение, используя опцию `numeric`. Это удобно, когда хочется получить приближенный график решения.