Как работает функция maximize в mathcad

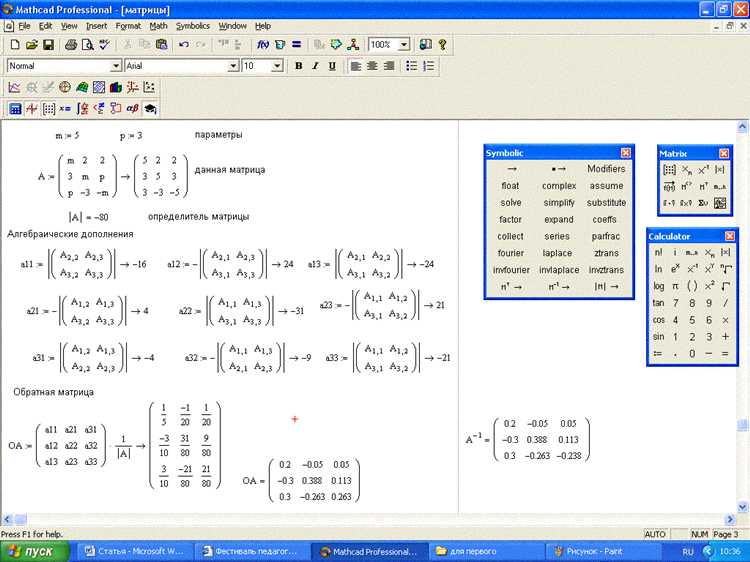
Функция maximize в Mathcad предназначена для поиска максимального значения заданной функции на заданном интервале или множестве условий. В основе её работы лежит численный метод оптимизации, который последовательно оценивает значения функции, изменяя аргументы в рамках ограничений, заданных пользователем.

Для корректного использования maximize требуется четкое определение области поиска – диапазона переменных и ограничений. Функция автоматически применяет алгоритмы градиентного подъема, обеспечивая быстрое и точное нахождение локальных максимумов. При этом важна предварительная оценка гладкости и выпуклости целевой функции, чтобы избежать сходимости к нежелательным экстремумам.

Практические рекомендации включают: тщательную подготовку модели с корректной постановкой ограничений, выбор адекватных начальных приближений и анализ полученного решения на предмет глобальности. Оптимизация с помощью maximize значительно упрощает сложные вычисления, позволяя концентрироваться на интерпретации результатов, а не на реализации алгоритмов.

Как задать целевую функцию для maximize в Mathcad

Для корректной работы функции maximize в Mathcad необходимо чётко определить целевую функцию – выражение, которое требуется максимизировать. Следуйте следующим рекомендациям:

1. Формат записи функции: целевая функция должна быть скалярным выражением, зависящим от одной или нескольких переменных. Например, f(x, y) := 3*x^2 + 2*y.

2. Использование именованных функций: лучше определить функцию отдельно через оператор присваивания :=. Это повышает читаемость и облегчает отладку.

3. Обязательное определение всех переменных: перед вызовом maximize задайте начальные значения или диапазоны переменных, участвующих в функции. Например, x := 1 или x ∈ [0,10].

4. Передача функции в maximize: в качестве первого аргумента передайте имя функции или непосредственно выражение. Например, maximize(f(x, y), x, y) или maximize(3*x^2 + 2*y, x, y).

5. Избегайте логических и векторных выражений: целевая функция должна возвращать числовое значение. Векторные, логические или матричные выражения вызовут ошибку.

6. Оптимизация сложных функций: при сложных вычислениях рекомендуется разбивать функцию на части и проверять результат каждой, чтобы убедиться, что целевая функция корректно вычисляется для любых допустимых значений переменных.

Правильно заданная целевая функция – основа для успешного применения maximize в Mathcad и получения точных результатов оптимизации.

Настройка ограничений при использовании maximize

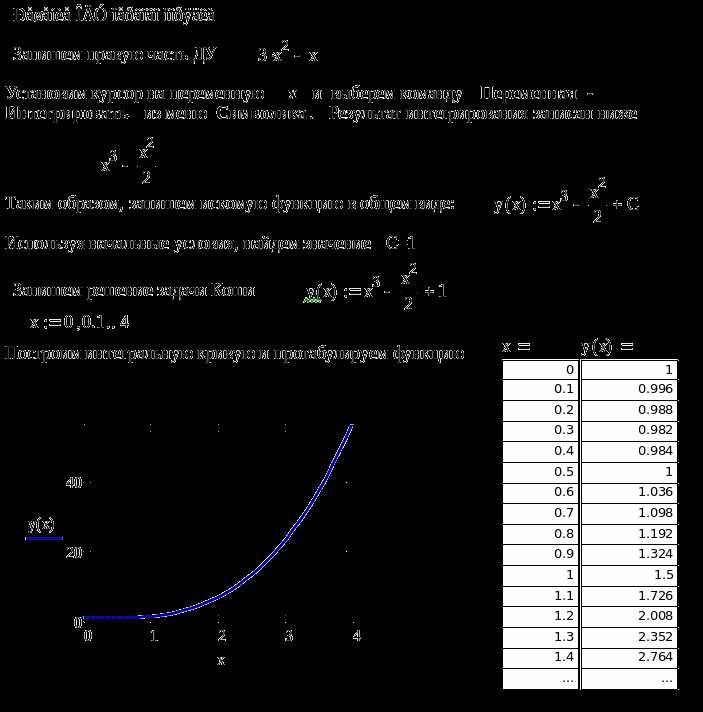
Функция maximize в Mathcad решает задачи оптимизации с ограничениями, которые задаются в виде уравнений или неравенств. Для корректной работы необходимо четко определить типы и форматы ограничений.

• Типы ограничений:
  • Жёсткие ограничения (равенства) – задаются через выражения вида g(x) = 0. Их необходимо формулировать в явной форме, без двойных знаков равенства.
  • Нежёсткие ограничения (неравенства) – задаются через g(x) ≤ 0 или g(x) ≥ 0. Mathcad поддерживает только односторонние неравенства, поэтому важно перевести все ограничения к одному виду.
• Формат задания:
  • Ограничения вводятся списком в виде массива функций, например, {g1(x), g2(x), …}.
  • Каждое ограничение должно быть функцией, возвращающей числовое значение.
• Рекомендации по оформлению ограничений:
  1. Используйте однородные переменные для всех ограничений, чтобы избежать конфликтов при вычислении.
  2. Избегайте сложных вложенных функций внутри ограничений – это снижает точность и скорость сходимости.
  3. Проверяйте корректность знаков неравенств, так как Mathcad не интерпретирует обратные знаки автоматически.
  4. Минимизируйте количество ограничений без необходимости – избыточные ограничения увеличивают вычислительную нагрузку.
• Проверка ограничений:
  • Перед вызовом maximize протестируйте каждое ограничение на допустимость, подставляя начальные значения переменных.
  • Ошибки в ограничениях приводят к невозможности нахождения решения или к выходу за границы допустимой области.

Типы переменных, поддерживаемые функцией maximize

Функция maximize в Mathcad работает с числовыми переменными, которые могут быть как скалярами, так и векторами или матрицами. Для оптимизации допустимы только вещественные числа с плавающей точкой; целочисленные переменные автоматически приводятся к типу с плавающей точкой.

Булевы значения и символьные переменные не поддерживаются в качестве оптимизируемых аргументов. Если такие типы включены в область поиска, это вызовет ошибку вычисления.

Переменные должны иметь фиксированную размерность на момент вызова maximize. Изменяемая или неопределённая размерность массива приведёт к сбою алгоритма. Рекомендуется использовать векторы или матрицы с четко заданной структурой данных.

Функция поддерживает оптимизацию по нескольким переменным одновременно, если они объединены в один вектор или матрицу. Разделение на отдельные переменные следует избегать, чтобы обеспечить корректную обработку.

Параметры с ограничениями (например, неотрицательность) должны быть заранее обработаны в пределах самой функции целевой, так как maximize не поддерживает явное задание ограничений на типы переменных.

Алгоритмы решения задач максимизации в Mathcad

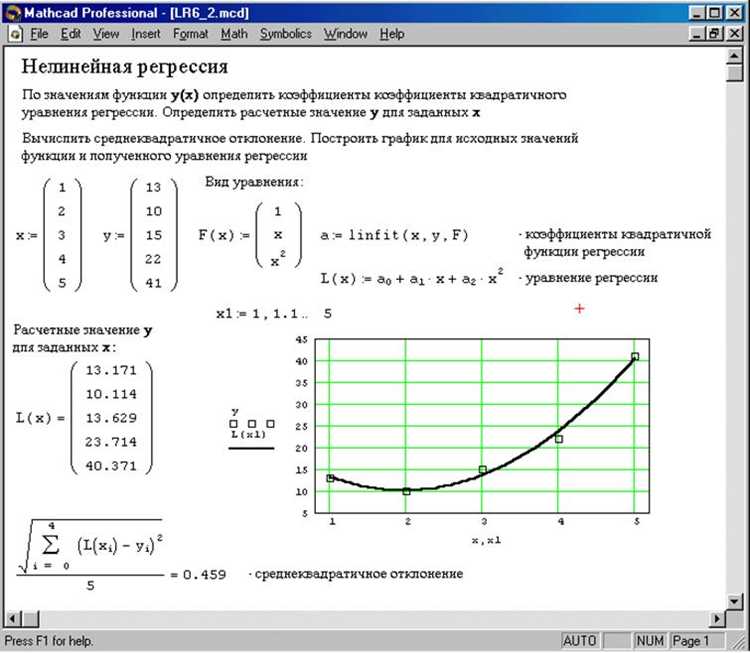
Mathcad применяет численные методы оптимизации, ориентированные на эффективный поиск глобального или локального максимума функции. Основной инструмент – функция maximize, которая использует модифицированные версии градиентных и эволюционных алгоритмов.

При максимизации в Mathcad важна точная постановка задачи: функция должна быть непрерывной и дифференцируемой для использования градиентных методов. Mathcad автоматически вычисляет градиенты, что ускоряет сходимость. Для задач с ограничениями применяется метод проекций, который удерживает решение внутри допустимой области.

Если функция имеет много локальных максимумов или не дифференцируема, Mathcad переключается на алгоритмы, основанные на методах случайного поиска и генетических алгоритмах. Эти алгоритмы менее чувствительны к гладкости и позволяют находить приближенный глобальный максимум.

Рекомендуется задавать начальные приближения максимально близко к предполагаемому решению – это ускоряет работу градиентных методов и повышает точность. При наличии ограничений следует явно формулировать их в параметрах функции maximize для корректного учета.

При работе с большими системами оптимизации полезно использовать параметр настройки точности и ограничения по числу итераций, что предотвращает излишние вычисления и снижает время обработки.

Таким образом, Mathcad предлагает гибкую комбинацию алгоритмов, которые автоматически адаптируются под структуру задачи и требования пользователя, обеспечивая баланс между скоростью и качеством решения.

Обработка ошибок и некорректных данных в maximize

Функция maximize в Mathcad требует строго заданных входных данных для корректного вычисления. Основные ошибки связаны с неверным форматом целевой функции, ограничений или начальных значений.

При передаче функции, не являющейся скалярной или возвращающей комплексные значения, maximize возвращает ошибку вычисления. Для предотвращения этого необходимо обеспечить, чтобы функция была вещественной и однозначно определённой в диапазоне оптимизации.

Некорректные или противоречивые ограничения приводят к невозможности поиска решения. Если границы не задают допустимую область (например, верхняя граница меньше нижней), maximize выдаст ошибку отсутствия решения. Рекомендуется проверять диапазоны до вызова функции и корректировать их вручную.

Отсутствие или неверное задание начальной точки оптимизации снижает устойчивость алгоритма и может привести к локальным экстремумам или ошибкам сходимости. Начальное значение должно находиться внутри допустимой области, иначе optimize автоматически не исправит его, а вызовет ошибку.

Ошибки в синтаксисе аргументов функции проявляются как сообщения компилятора Mathcad. Чтобы избежать, важно соблюдать формат вызова maximize, чётко указывая функцию, переменные и ограничения, без лишних символов или пробелов.

Рекомендация: включать проверку входных данных через встроенные условия и функции логического контроля, чтобы заблаговременно выявлять ошибки и корректировать параметры перед запуском maximize.

В случае нестандартных ошибок стоит обращаться к журналу вычислений Mathcad, который содержит подробные сведения о причинах сбоя и помогает диагностировать проблему на уровне модели.

Оптимизация параметров запуска maximize для повышения точности

Для повышения точности функции maximize в Mathcad критично настроить параметры запуска, отвечающие за начальные условия и ограничения. Первое, на что нужно обратить внимание – выбор начального приближения. Оптимальное значение начального вектора влияет на скорость сходимости и результат: рекомендуется задавать стартовые точки, максимально приближенные к предполагаемому экстремуму, особенно в задачах с несколькими локальными максимумами.

Параметр точности (Tolerance) задает допустимую погрешность при вычислениях. Для повышения точности следует уменьшить значение Tolerance, например, с 10⁻⁴ до 10⁻⁶, что приведет к более детальной проверке условий сходимости, но увеличит время вычислений. Важно балансировать точность и производительность в зависимости от требований задачи.

Параметры ограничений (Constraints) должны быть заданы с максимально возможной точностью. Нечеткие или слишком общие ограничения приводят к ошибкам в вычислениях и неоптимальным результатам. Используйте равенства и неравенства, которые точно отражают физическую или математическую природу задачи.

Режим решения (Solver mode) можно переключать между стандартным и расширенным. Расширенный режим активирует более сложные алгоритмы поиска экстремума, что полезно для функций с сильной нелинейностью и несколькими переменными. Для таких задач рекомендуется включать расширенный режим, несмотря на возросшую нагрузку на систему.

Использование градиентных методов в настройках maximize требует точного вычисления производных. При отсутствии аналитических формул желательно задать численное приближение с минимальным шагом, чтобы снизить погрешность градиента.

Также имеет значение установка максимального числа итераций. Слишком малое значение приводит к преждевременному завершению работы, а избыточное – к неоправданному расходу времени. Рекомендуется анализировать поведение функции на тренировочных данных, чтобы подобрать оптимальное значение итераций.

Примеры применения maximize в инженерных расчетах

В инженерии функция maximize в Mathcad применяется для решения задач оптимизации с целью определения максимального значения целевой функции при заданных ограничениях. Например, при проектировании балки под нагрузкой maximize позволяет найти максимальную нагрузку, которую может выдержать конструкция, учитывая прочностные характеристики материала и геометрию сечения.

В термодинамике с помощью maximize вычисляют максимальную эффективность теплового двигателя, оптимизируя параметры рабочего цикла при фиксированных граничных условиях. Это позволяет определить наилучшее соотношение давления и температуры для достижения максимальной полезной работы.

При расчете электроцепей maximize применяется для определения максимальной мощности, которую может отдавать источник питания без выхода из режимов безопасности. В этом случае учитываются параметры элементов цепи, такие как сопротивление и допустимая нагрузка.

В задачах аэродинамики функция maximize помогает найти максимальное значение подъемной силы при заданных углах атаки и скоростях потока, что важно для оптимизации профиля крыла и повышения летных характеристик самолета.

Для инженерных систем автоматизации maximize позволяет оптимизировать производительность процесса, например, максимизировать скорость подачи материала на конвейере при ограничениях по мощности двигателя и безопасности эксплуатации оборудования.

Вопрос-ответ:

Что именно делает функция maximize в Mathcad?

Функция maximize ищет максимальное значение заданной функции, изменяя переменные в пределах установленных ограничений. Она автоматически перебирает варианты и возвращает наибольший результат, который можно получить при данных условиях.

Какие типы задач можно решать с помощью maximize в Mathcad?

Функция применяется для оптимизации, то есть для поиска наибольшего значения целевой функции. Это полезно в экономике, инженерии и науках, где необходимо определить максимальную прибыль, производительность или другие показатели при заданных ограничениях.

Как задать ограничения при использовании maximize?

Ограничения указываются в виде уравнений или неравенств, которые задаются вместе с функцией. Mathcad учитывает эти условия при поиске максимума, исключая значения переменных, не удовлетворяющие ограничениям.

Можно ли использовать функцию maximize с несколькими переменными? Как это делается?

Да, maximize поддерживает работу с несколькими переменными. Для этого переменные объявляются в виде вектора или списка, а сама целевая функция зависит от всех этих переменных. Mathcad затем ищет максимум по всем параметрам одновременно.

Какие ошибки наиболее часто возникают при работе с maximize, и как их избежать?

Типичные проблемы — неправильно заданные ограничения, несоответствие типов данных или отсутствие начального приближения для поиска. Чтобы минимизировать ошибки, важно тщательно проверить формулы и задать начальные значения, особенно при сложных системах уравнений.