Ряд Тейлора позволяет представить функцию в виде бесконечной суммы её производных, вычисленных в одной точке, что упрощает анализ и приближённые вычисления. В Mathcad процесс разложения автоматизирован, однако понимание каждого этапа важно для точного контроля результата.
Для начала необходимо задать функцию и определить точку разложения, обычно обозначаемую как x₀. Далее вычисляются производные функции нужного порядка, которые Mathcad вычисляет с помощью встроенных операторов. Ключевой момент – правильное использование переменных и операторов, чтобы избежать ошибок в вычислениях.
Mathcad позволяет не только получить разложение в виде формулы, но и визуализировать степень приближения ряда к исходной функции на выбранном интервале. Рекомендуется выполнять проверку с помощью построения графиков функции и её ряда, а также контролировать погрешность, чтобы оценить качество аппроксимации.
Как задать функцию в Mathcad для последующего разложения
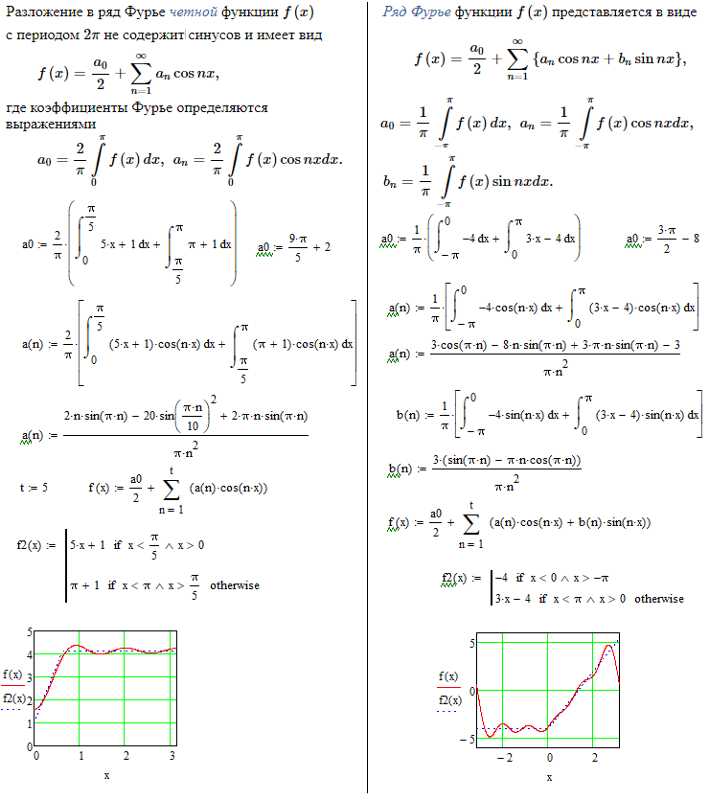
Для точного разложения функции в ряд Тейлора в Mathcad необходимо корректно определить функцию. Ввод осуществляется через объявление переменной с использованием оператора присваивания «:=». Например, для функции f(x) = sin(x) + x^2 следует ввести f(x) := sin(x) + x^2. При этом важно, чтобы переменная x была свободной переменной, не имевшей предварительного значения.
Используйте встроенные математические операторы и функции Mathcad, учитывая регистр символов: sin, cos, exp и др. Для степеней применяйте символ «^», например, x^3. Обязательно проверяйте корректность синтаксиса: отсутствуют лишние пробелы в выражениях, закрыты скобки.
Если функция зависит от нескольких переменных, определите её с явно заданными аргументами, например, g(x, y) := x^2 + y^2. Однако для разложения в ряд Тейлора по одной переменной выделите соответствующую переменную.
Перед разложением убедитесь, что функция вычисляется без ошибок, выполнив проверочный расчет для конкретного значения аргумента, например, f(0). В случае ошибки исправьте синтаксис или определение переменных.
Для последующего применения инструмента разложения в Mathcad функция должна быть введена именно в форме присваивания с параметрами, а не в виде числового массива или графика.
Настройка точки разложения и выбор порядка ряда Тейлора
В Mathcad для разложения функции в ряд Тейлора необходимо задать точку разложения – значение переменной, вокруг которого строится ряд. Обычно это фиксируется параметром, например, x0. Выбор x0 влияет на точность аппроксимации: чем ближе аргумент функции к x0, тем точнее приближение. В интерфейсе Mathcad точку разложения задают непосредственно в команде построения ряда, указывая числовое значение.
Порядок ряда определяет количество учитываемых членов разложения. В Mathcad задается числом n, которое указывает максимальную степень производной в ряде. При выборе порядка учитывайте гладкость функции и требуемую точность: низкий порядок (2–4) подходит для локальных приближений в небольшой окрестности, высокий (6 и более) – для более широких интервалов, но при этом растет вычислительная нагрузка и возможны численные ошибки.
Для оценки оптимального порядка полезно сравнить значения функции и ряда в нескольких точках, а также вычислить остаточный член (если доступно). В Mathcad остаток ряда можно получить через встроенные функции дифференцирования и интегрирования, что помогает контролировать погрешность.
Рекомендуется начинать с порядка 3–5 и постепенно увеличивать, отслеживая сходимость ряда. Точку разложения выбирают так, чтобы она совпадала с областью интереса или с точками, где функция имеет важные особенности (например, экстремумы). В случаях с переменными точками лучше использовать параметры Mathcad для динамического изменения x0 и n, что облегчает анализ поведения аппроксимации.
Использование встроенной функции Taylor в Mathcad

В Mathcad функция Taylor автоматически строит разложение заданной функции в ряд Тейлора вокруг выбранной точки с указанием порядка разложения. Формат вызова: Taylor(функция, переменная, точка, порядок). Аргумент функция задаётся в виде выражения с переменной, переменная – символ, по которому выполняется разложение, точка – значение, около которого строится ряд, порядок – количество учитываемых членов.
Для корректной работы Taylor переменная должна быть определена в виде символической переменной Mathcad. Точка разложения может быть как числом, так и переменной с конкретным значением. При использовании нулевой точки (разложение в 0) упрощается вычисление коэффициентов, что полезно при анализе около начала координат.
Результатом работы функции является символьное выражение, представляющее сумму членов ряда с точностью до заданного порядка. Для дальнейших вычислений или построения графиков рекомендуется использовать преобразование результата в функцию с помощью expand или simplify, что облегчает восприятие и минимизирует возможные ошибки округления.
Для повышения точности рекомендуется задавать порядок разложения не ниже 4, особенно при исследовании сложных функций с высокой степенью нелинейности. Если функция содержит параметрические выражения, перед вызовом Taylor следует подставить конкретные значения параметров, чтобы избежать неопределённостей в разложении.
Для проверки корректности результата можно сравнить значение исходной функции и разложения в точках, близких к точке разложения, используя встроенные средства вычислений Mathcad. При расхождении лучше увеличить порядок или изменить точку разложения.
Проверка и интерпретация результата разложения

После выполнения разложения функции в ряд Тейлора в Mathcad необходимо проверить корректность результата. Сравните исходное выражение с суммой ряда, вычисленной для нескольких значений переменной в окрестности точки разложения. Ошибки обычно возникают из-за неверного выбора порядка разложения или неправильной точки разложения.
Для оценки точности используйте функцию вычисления остаточного члена ряда или сравните значение разложенной суммы с исходной функцией при нескольких значениях аргумента. Если разница превышает допустимый уровень, увеличьте степень ряда или уточните область применения разложения.
Интерпретируйте коэффициенты ряда: первый член – значение функции в точке разложения, следующий – производные соответствующих порядков, делённые на факториал. Проверка соответствия этих коэффициентов аналитически помогает выявить ошибки ввода функции или параметров разложения.
Mathcad позволяет построить графики исходной функции и её аппроксимации рядом Тейлора. Визуальное сопоставление кривых на интервале разложения позволяет увидеть пределы применимости и характер погрешности. Если графики существенно расходятся даже близко к точке разложения, необходимо пересмотреть параметры ряда.
Внимательно следите за точкой разложения: смещение от неё увеличивает ошибку аппроксимации, особенно при малой степени ряда. Практика показывает, что для функций с быстрыми изменениями требуется более высокий порядок разложения.
Визуализация функции и её разложения на графике в Mathcad

Для наглядного сравнения исходной функции и её разложения в ряд Тейлора в Mathcad создайте график с двумя кривыми: одна – оригинальная функция, вторая – частичная сумма ряда. Введите функцию, например, f(x) := sin(x), и определите частичную сумму ряда Тейлора с нужным числом членов. Например, для 5 членов:
T5(x) := x - x^3/3! + x^5/5! - x^7/7! + x^9/9!
Затем выберите диапазон отображения, например, от -2π до 2π. Для построения графика создайте объект графика XY и задайте для оси X нужный интервал с шагом, например, 0.1. В поле функции введите два выражения, разделённые запятой: f(x), T5(x).
Mathcad отобразит две кривые разными цветами. Для точного сопоставления используйте легенду, которую можно добавить через контекстное меню графика, указав подписи “Исходная функция” и “Ряд Тейлора”.
Если требуется проанализировать точность аппроксимации, добавьте на график третью кривую – абсолютную разницу между функцией и рядом: Abs(f(x) - T5(x)). Для визуального удобства лучше использовать отдельный график с вертикальной осью в логарифмическом масштабе, чтобы выявить даже малые отклонения.
Для динамического исследования влияния числа членов ряда используйте слайдер (ползунок), связывая количество членов с вычислением частичной суммы. Это позволяет мгновенно увидеть изменение точности аппроксимации при увеличении или уменьшении членов ряда.
Исправление ошибок при вычислении ряда Тейлора
При работе с рядом Тейлора в Mathcad часто возникают ошибки, связанные с неправильной постановкой задачи или особенностями численных методов. Для устранения проблем важно последовательно проверить ключевые этапы вычисления.
- Проверка исходной функции и точки разложения:
- Убедитесь, что функция задана корректно, без синтаксических и логических ошибок.
- Точка разложения должна находиться в области определения функции.
- Проверьте, не является ли точка особой (например, точкой разрыва или неопределённости).
- Правильное вычисление производных:
- Используйте встроенные операторы Mathcad для дифференцирования, избегая ручного ввода производных.
- Проверьте значения производных в точке разложения на предмет конечности и корректности.
- Если производные вычисляются численно, увеличьте точность расчетов.
- Корректное построение ряда:
- Убедитесь, что формула для члена ряда реализована согласно теории: (f^(n)(a)/n!) * (x — a)^n.
- Обратите внимание на индексацию – в Mathcad счёт может начинаться с 0 или 1, учитывайте это при построении цикла.
- Используйте функцию factorial(n) для вычисления факториала, чтобы избежать ошибок в знаменателе.
- Проверка области сходимости:
- Рассчитайте радиус сходимости ряда, если это возможно.
- Не вычисляйте значения ряда за пределами радиуса сходимости, чтобы избежать больших отклонений.
- Анализ погрешностей:
- Сравните результаты ряда с точным значением функции в контрольных точках.
- Увеличьте количество членов ряда для повышения точности.
- Обратите внимание на округления и числовые ошибки, применяя дополнительные знаки после запятой.
Соблюдение этих рекомендаций в Mathcad позволяет минимизировать ошибки и повысить точность разложения функции в ряд Тейлора.
Примеры практического применения ряда Тейлора в Mathcad
Ряд Тейлора в Mathcad эффективно применяется для приближённого вычисления значений сложных функций, когда аналитическое решение затруднено или отсутствует. Например, аппроксимация экспоненты exp(x) в окрестности нуля позволяет быстро получить числовые значения с заданной точностью без вызова встроенных функций.
В инженерных расчетах ряд Тейлора используется для упрощения выражений, содержащих тригонометрические функции, такие как sin(x) и cos(x). Разложение в Mathcad помогает выявить ведущие члены и оценить погрешность, что критично при проектировании систем с малыми колебаниями.
Для решения дифференциальных уравнений методом численного интегрирования в Mathcad разложение в ряд Тейлора позволяет создавать локальные приближения решений на малых интервалах, обеспечивая контроль точности за счёт количества учитываемых членов ряда.
При анализе поведения функций вблизи особых точек (например, при x → 0) Mathcad позволяет быстро получить асимптотические выражения, что облегчает понимание свойств функции и построение графиков без искажения из-за численных ошибок.
Ряд Тейлора применим и в экономическом моделировании, когда необходимо аппроксимировать функции спроса или предложения с помощью полиномов для последующей оптимизации и анализа чувствительности.
Для практического применения рекомендуется в Mathcad:
– использовать встроенную функцию series() с указанием точки разложения и порядка ряда;
– проверять сходимость ряда и оценивать остаточный член для гарантии необходимой точности;
– сравнивать результаты приближения с исходными значениями функции для контроля ошибок.
Вопрос-ответ:
Как в Mathcad задать функцию для разложения в ряд Тейлора?
Для начала нужно определить функцию с помощью стандартного синтаксиса Mathcad, например, записав f(x):= выражение. После этого можно воспользоваться встроенной командой для разложения в ряд, указав точку разложения и количество членов ряда. Важно, чтобы функция была корректно введена и определена в области интереса.
Какие параметры необходимо указать при построении ряда Тейлора в Mathcad?
При разложении функции нужно задать точку, вокруг которой выполняется разложение (обычно это значение переменной, например, x=0 или другое), а также количество членов ряда, которое определяет точность приближения. В Mathcad эти параметры вводятся в соответствующие поля команды разложения, либо задаются вручную в формуле, если используется символьный редактор.
Можно ли получить численное приближение ряда Тейлора в Mathcad, и как это сделать?
Да, Mathcad позволяет вычислить численное значение ряда Тейлора, подставив конкретное значение переменной. Для этого после получения выражения ряда нужно заменить переменную на нужное число и выполнить вычисление. Если используется символическое разложение, иногда требуется переключиться на численные вычисления с помощью встроенных функций округления или преобразования.
Как проверить корректность разложения функции в ряд Тейлора в Mathcad?
Проверка может быть выполнена сравнением графиков исходной функции и суммы первых членов ряда на выбранном интервале. Кроме того, можно вычислить значения функции и ряда в нескольких точках и сравнить результаты. Если они близки, значит разложение выполнено правильно и приближение адекватно.
Какие ошибки часто встречаются при работе с рядом Тейлора в Mathcad и как их избежать?
Типичные ошибки связаны с неверным заданием функции (например, синтаксические ошибки или неправильные обозначения), выбором неподходящей точки разложения, а также с недостаточным числом членов ряда, из-за чего приближение может быть плохим. Чтобы избежать проблем, следует внимательно проверять ввод, понимать особенности функции и корректно выбирать параметры разложения.