Как решать системы дифференциальных уравнений в mathcad

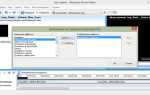
Mathcad предоставляет мощный инструмент ОDEsolve для численного решения систем обыкновенных дифференциальных уравнений (ОДУ). Поддержка как начальных условий, так и параметров позволяет моделировать сложные динамические процессы без необходимости программирования. Операторы решения интегрированы в среду с визуальным оформлением, что делает процесс максимально наглядным.

При задании системы уравнений переменные обозначаются как вектор-функции. Например, для системы второго порядка удобно использовать вектор y, содержащий функции y₁(t), y₂(t), где каждая функция описывает отдельное дифференциальное уравнение. Форма записи соответствует синтаксису: y′(t) = f(t, y), где производные представляются в виде вектора. Ввод начальных условий осуществляется через отдельный вектор y₀.

Для корректной работы функции Odesolve важно предварительно определить все переменные и задать диапазон изменения аргумента. Рекомендуется использовать именованные диапазоны времени t := 0, 0.01 .. 10 и задавать сетку интегрирования с достаточной плотностью, чтобы избежать численных артефактов. Mathcad автоматически использует адаптивный шаг, но чрезмерная разреженность узлов приводит к снижению точности.

Для анализа результатов удобно строить графики компонент решения напрямую, ссылаясь на элементы вектора y(t). Это позволяет быстро выявить особенности поведения системы, такие как устойчивость, колебательность или выход на стационарное состояние. Дополнительно рекомендуется использовать встроенные функции rkfixed и bulstoer для сравнения точности решений различными методами.

Пошаговое задание системы дифференциальных уравнений в Mathcad

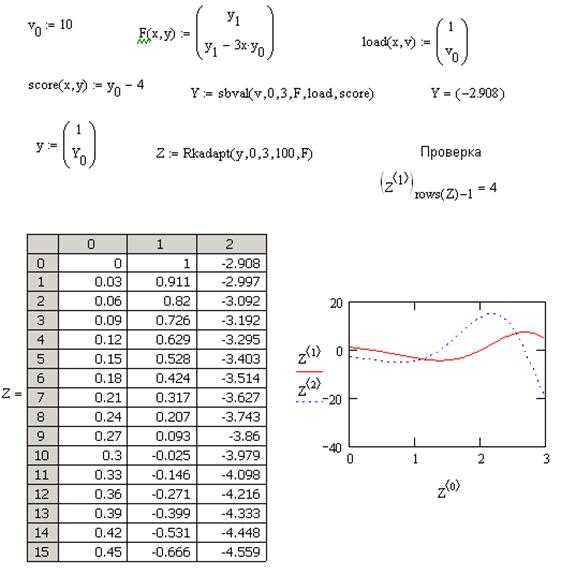
Для задания системы дифференциальных уравнений в Mathcad необходимо использовать блок Given-Find или оператор odesolve в сочетании с функцией начальных условий. Ниже представлен пошаговый алгоритм работы.

1. Определите переменные:
   • Задайте независимую переменную, например: t :=
   • Определите неизвестные функции, например: y(t), z(t)
2. Запишите производные:
   • Используйте обозначение y'(t) или y′, вводя апостроф с клавиатуры.
   • Для второй производной – два апострофа: y''(t).
3. Сформулируйте уравнения системы:
   • Например: y'(t) = z(t), z'(t) = -y(t)
4. Задайте начальные условия:
   • Присвойте значения: y(0) := 1, z(0) := 0
5. Создайте оператор Given:
   • Вставьте его с панели «Math» или клавишей Ctrl + G
   • Внутри него введите уравнения без символа равенства (используйте символ ≡ – эквивалентность)
6. Используйте функцию oDesolve:
   • Пример: sol := odesolve(t, y, z)

Если используется solve block (Given-Find), то вместо odesolve применяют Find(y, z) и обязательно указывают дифференциальные уравнения в форме y'(t) ≡ z(t) и z'(t) ≡ -y(t).

Для численного решения и графического отображения решений предпочтительно использовать встроенные графики: выбирайте ось X как t, а ось Y – как значения sol[0] и sol[1]] для функций y(t) и z(t) соответственно.

Использование оператора ODEsolve для численного решения

В Mathcad оператор odeSolve применяется для численного интегрирования систем обыкновенных дифференциальных уравнений первого порядка. Он используется совместно с блоком Given, где задаются начальные условия и уравнения системы.

Формат вызова: Y := Odesolve(t, Y0, tf), где t – независимая переменная, Y0 – вектор начальных условий, tf – конечное значение интервала интегрирования. Оператор возвращает функцию, которую можно вызывать для получения численного значения решения при заданных значениях t.

Перед использованием необходимо определить векторную функцию производных. Например, при решении системы из двух уравнений y₁'(t) = f₁(t, y₁, y₂), y₂'(t) = f₂(t, y₁, y₂), объявляется вектор F(t, Y) := [f₁(t, Y[0], Y[1]), f₂(t, Y[0], Y[1])], где Y – вектор неизвестных функций.

Начальные условия задаются в виде Y0 := [y₁₀, y₂₀], где y₁₀, y₂₀ – значения функций в начальный момент времени. После вызова Y := Odesolve(t, Y0, tf), полученная функция Y(t) возвращает вектор решений при любом значении t на интервале интегрирования.

Для повышения точности решения можно явно задать метод интегрирования, добавив параметр, например "Radau" или "BDF". Пример: Odesolve(t, Y0, tf, "BDF"). Метод "Adams" предпочтителен при гладких решениях, "BDF" – при жёстких системах.

Следует избегать повторного определения переменных внутри блока Given – это приводит к ошибкам решения. Убедитесь, что функции правых частей системы непрерывны и дифференцируемы в рабочем интервале.

Для визуализации результатов рекомендуется строить графики по компонентам возвращаемого вектора: plot(Y(t)[0], Y(t)[1]). Это упрощает анализ поведения системы без необходимости ручного преобразования данных.

Настройка начальных условий и диапазона переменной

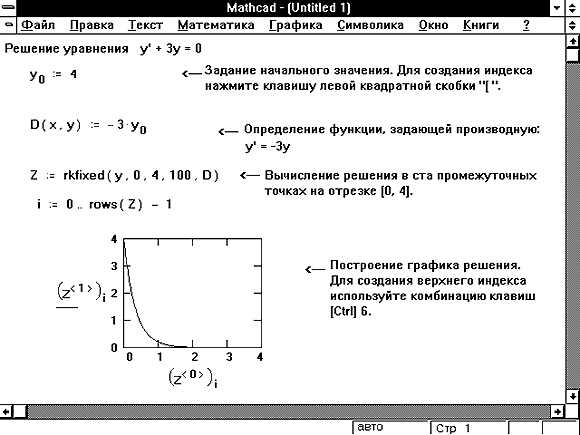
Для корректного решения системы дифференциальных уравнений в Mathcad необходимо задать вектор начальных условий и определить диапазон независимой переменной. Начальные условия задаются в виде вектора, содержащего значения всех искомых функций при заданном начальном значении аргумента. Например, для системы из двух уравнений при x = 0, начальные условия задаются так: Y₀ := [1, 0].

Диапазон переменной задается с использованием оператора диапазона. Пример: x := 0, 0.1 .. 10 устанавливает шаг 0.1 от 0 до 10. Этот шаг влияет на точность численного решения и плотность отображения графиков. Для жестких систем желательно использовать меньший шаг, чтобы избежать потери устойчивости.

Вызов функции rkfixed или odesolve требует согласованности между длиной вектора начальных условий и количеством уравнений в системе. Несоответствие приводит к ошибке вычислений. Также необходимо удостовериться, что начальное значение переменной совпадает с точкой, на которой заданы начальные условия.

Для систем, чувствительных к начальному значению, полезно использовать параметризацию: начальные условия задаются через переменные, которым можно оперативно назначать различные значения. Это облегчает анализ влияния начальных условий на поведение системы.

Избегайте излишне широких диапазонов переменной при первом запуске модели. Сначала используйте ограниченный интервал, чтобы проверить устойчивость и поведение системы, после чего при необходимости расширяйте его. Это минимизирует время вычислений и упрощает отладку.

Отображение результатов в виде графиков и таблиц

Для анализа решений систем дифференциальных уравнений в Mathcad критически важно визуализировать поведение переменных во времени. Используйте встроенный компонент 2D-графика: в качестве аргумента по оси X указывайте независимую переменную (например, t), а по оси Y – компоненты вектора решения.

Чтобы построить график всех компонент системы, определите матрицу результатов как функцию от времени: например, Y(t) := rkfixed(...), где rkfixed – метод Рунге-Кутты. Далее примените вызов plot(Y[0, t), Y[1, t), ..., Y[n, t)). Mathcad позволяет задавать разные цвета и стили линий через свойства графика без необходимости скриптов или программирования.

Для точечного анализа значений используйте текстовые матрицы. Преобразуйте массив решения в вид stack(t, Y[0, t), Y[1, t), ...) с последующим отображением с помощью команды Table. Включите форматирование чисел до необходимого количества знаков после запятой через локальные настройки отображения, чтобы избежать визуального шума.

Не размещайте график и таблицу рядом: Mathcad не оптимизирован для плотного размещения элементов. Сначала анализируйте график, затем переходите к таблице для уточнений и проверки точных значений.

Обработка ошибок при решении систем уравнений

Mathcad не всегда может корректно решить систему дифференциальных уравнений из-за ошибок, связанных с форматом ввода, типом переменных или некорректной инициализацией. При использовании встроенной функции Odesolve критично соблюдать правильный синтаксис: уравнения должны быть заданы в виде выражений с производными через символ апострофа ('), а не как уравнения с равенством.

Распространённая ошибка – использование числового значения вместо символического в граничных условиях. Например, при попытке задать условие вида x(0) = 1 в блоке определения уравнений может возникнуть конфликт типов, если переменная x не была предварительно обозначена как функция.

Нельзя использовать глобальные переменные, определённые вне блока Given, если они могут быть переопределены внутри него. Это приводит к неоднозначности решения. Все параметры системы должны быть локализованы и инициализированы внутри одного вычислительного блока.

При наличии ошибок Mathcad может выдавать сообщения вроде “This value must be a scalar” или “Too few initial conditions”. В первом случае это указывает на попытку подстановки векторного выражения вместо скалярного; во втором – на недостаточное количество начальных условий. Для системы из n уравнений требуется ровно n независимых начальных условий.

Рекомендуется перед решением визуализировать функции с помощью plot для оценки адекватности решения и быстрого выявления численных выбросов или неустойчивостей. Также важно контролировать шаг интегрирования: уменьшение шага может устранить ошибку сходимости, но при слишком малом шаге возможно накопление вычислительной погрешности.

Оптимальный подход – пошаговая отладка: начните с простой системы, постепенно добавляя уравнения. При каждом этапе проверяйте корректность и поведение решения. Это позволяет локализовать источник ошибки без необходимости полной переработки модели.

Сравнение различных методов интегрирования в Mathcad

Mathcad предоставляет несколько численных методов интегрирования систем дифференциальных уравнений: RKFixed, Rkadapt, Radau и Adams. Каждый из них имеет свои особенности и подходит для различных типов задач.

RKFixed – метод Рунге-Кутты с фиксированным шагом. Он эффективен при гладких решениях и известной длине шага. Однако при наличии жёстких участков интегрирование становится неустойчивым, а уменьшение шага резко увеличивает время расчёта.

Rkadapt использует адаптивный шаг, автоматически регулируя точность. При решении задач с резкими изменениями функции обеспечивает высокую точность при разумном времени расчёта. Этот метод предпочтителен для большинства инженерных задач, не содержащих жёстких уравнений.

Radau – имплицитный метод, подходящий для жёстких систем. Он требует больше вычислительных ресурсов на каждом шаге, но позволяет использовать большие интервалы при стабильном решении. Особенно эффективен при моделировании химических реакций и электрических цепей с сильно различающимися постоянными времени.

Adams – многошаговый метод, хорошо работающий при плавных решениях. Начальная фаза требует предварительного расчёта с использованием метода Рунге-Кутты. Метод чувствителен к нестабильностям и менее устойчив при резких изменениях решения.

Рекомендации по выбору:

• Используйте RKFixed, если известен оптимальный шаг и решение гладкое.
• Выбирайте Rkadapt для большинства стандартных задач.
• Применяйте Radau при жёстких системах.
• Adams – для длительного моделирования с постоянными параметрами.

Для сравнения методов на практике рекомендуется провести интегрирование одного и того же уравнения с каждым методом, измерив точность и время расчёта. Это позволит подобрать оптимальный метод для конкретной задачи с учётом доступных вычислительных ресурсов.

Вопрос-ответ: