Как решать уравнения в maple

Maple – мощная система компьютерной алгебры, оптимизированная для точного и символического решения уравнений различных типов. В работе с ней важно чётко понимать структуру уравнения и специфику используемых команд. Для начала необходимо определить вид уравнения: линейное, квадратное, дифференциальное или алгебраическое, так как в Maple применяются разные функции и методы для каждого из них.

Правильная постановка уравнения в Maple требует точного синтаксиса, например, использование символа двоеточия для присваивания и запятых для разделения аргументов. Для систем уравнений solve принимает список уравнений в фигурных скобках и список неизвестных. При работе с дифференциальными уравнениями используются специализированные пакеты, такие как DEtools, которые расширяют возможности стандартных команд и позволяют решать задачи с начальными условиями.

Как решать уравнения в Maple: пошаговая инструкция

Для решения уравнений в Maple используйте встроенную функцию solve. Ниже приведён подробный порядок действий.

1. Запустите Maple и откройте новый документ.
2. Определите уравнение в формате Maple. Например, для уравнения 2*x + 3 = 7 введите:

   eq := 2*x + 3 = 7;

3. Вызовите функцию решения:

   solve(eq, x);

   Здесь eq – уравнение, x – переменная, которую нужно найти.

4. Для решения систем уравнений задайте их как список или множество:

   sys := {x + y = 5, x - y = 1};

   Затем вызовите

   solve(sys, {x, y});

5. Если нужно получить решения в численном виде, используйте функцию fsolve:

   fsolve(eq, x);

6. Для уравнений с параметрами указывайте переменные и параметры явно:

   solve(a*x^2 + b*x + c = 0, x);

7. Для получения всех корней (в том числе комплексных) добавьте опцию complex:

   solve(eq, x, complex);

8. При работе с тригонометрическими или другими уравнениями с множеством решений используйте параметрическое решение:

   solve(sin(x) = 0, x, explicit);

9. Для упрощения результата применяйте функцию simplify:

   simplify(solve(eq, x));

Эти шаги обеспечивают точное и быстрое получение решений в Maple без лишних действий.

Запуск Maple и создание нового документа для решения уравнений

Для начала работы откройте программу Maple через меню Пуск или ярлык на рабочем столе. После запуска появится окно приветствия. Чтобы создать новый документ, выберите в главном меню пункт File → New Worksheet. Это откроет пустой рабочий лист, готовый к вводу математических выражений.

Для удобства рекомендуется сразу задать тип документа – рабочий лист (worksheet), а не документ с текстом (document mode), так как первый оптимален для вычислений и пошагового решения уравнений. В панели инструментов убедитесь, что выбран режим «Math», который обеспечивает корректный ввод математических формул.

Для удобства сохраните файл через File → Save As в нужной папке с расширением *.mw. Это позволит сохранить промежуточные результаты и при необходимости вернуться к работе позже.

Ввод и форматирование уравнений в Maple

Для корректного ввода уравнений в Maple используйте оператор присваивания := только при необходимости создания переменных. Уравнения задаются через знак равенства =, например: eq := x^2 + 3*x - 4 = 0;. Для степеней применяйте символ ^, а не повторение символов или другие альтернативы.

Для группировки выражений используйте круглые скобки (), что предотвращает ошибки при приоритетах операций. Например, в выражении (x + 1)^2 скобки обязательны.

Обратите внимание на тип символов: переменные и функции вводятся без пробелов, а операторы должны отделяться пробелами для читаемости, например: sin(x) + 2*x = 5. Встроенные функции Maple чувствительны к регистру – sin и Sin – разные объекты.

Используйте двоеточие с запятой ; для завершения команд. Для ввода нескольких уравнений в систему применяйте запятую внутри фигурных скобок, например: {x + y = 2, x - y = 0}. Это упростит последующую передачу системы в решатели.

Чтобы избежать неявных ошибок, всегда проверяйте корректность ввода через команду is(equation) – она возвращает true, если выражение действительно уравнение.

При вводе рациональных чисел используйте дроби в формате 1/2 вместо десятичных дробей, так Maple сохраняет точность и упрощает вычисления.

Использование команды solve для поиска корней уравнений

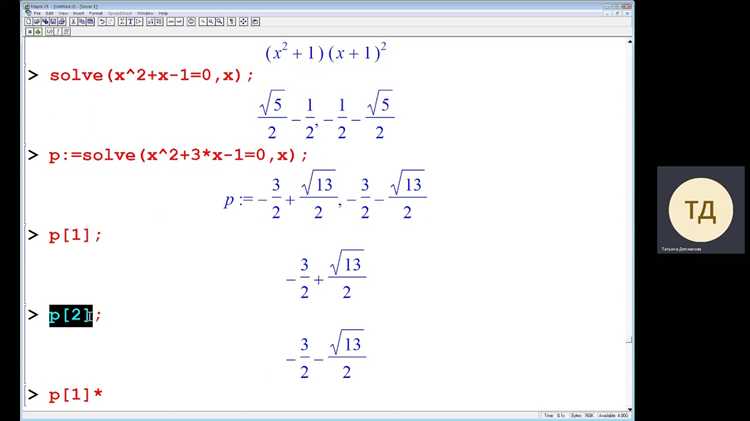
Команда solve в Maple предназначена для точного или аналитического поиска корней уравнений. Синтаксис базового вызова выглядит так: solve(уравнение, переменная). Важно указывать переменную явно, чтобы Maple понимал, по какой неизвестной производить поиск.

Для линейных и алгебраических уравнений команда возвращает все корни в виде списка или множества. Если уравнение многозначное, результатом будет множество решений. В случае систем уравнений используется форма solve({уравнение1, уравнение2, ...}, {переменная1, переменная2, ...}).

При работе с уравнениями, содержащими параметры, можно задать условия для них с помощью дополнительных ограничений в составе системы или использовать опцию assume для уточнения области значений параметров. Без этого Maple выдаст общее решение в символической форме.

Для уравнений, не имеющих аналитического решения, команда solve вернёт выражение без численных значений. В таких случаях рекомендуется применять fsolve для численного приближения корней.

Если требуется получить решения в определённом интервале, solve не поддерживает такие ограничения напрямую. Лучше сначала преобразовать уравнение, ограничив переменную через дополнительное условие или использовать fsolve с указанием диапазона.

При использовании solve с тригонометрическими уравнениями важно помнить, что результат может содержать общее решение с параметрами. Для конкретных решений следует задавать условия на параметры или использовать численные методы.

Пример поиска корней квадратного уравнения: solve(x^2 - 5*x + 6 = 0, x) вернёт два корня: x=2 и x=3.

При решении уравнений с комплексными корнями можно получить решения в комплексной форме, если явно не ограничить область значений переменной. Для работы только с вещественными корнями добавьте условие assume(x, real) или используйте фильтрацию результата.

Решение систем уравнений с помощью Maple

Для решения систем уравнений в Maple используется функция solve. В качестве аргумента необходимо передать список или множество уравнений и список переменных, по которым нужно найти решения.

Пример решения системы из двух уравнений с двумя переменными:

solve({x + y = 5, x - y = 1}, {x, y});

Результат будет представлен в виде списка пар значений переменных. Если требуется получить численное приближение, применяется функция fsolve с теми же аргументами.

Для систем с нелинейными уравнениями допустимо использование тех же функций. Maple автоматически анализирует уравнения и выдает все найденные решения или указывает отсутствие решений.

Если система слишком сложная, можно использовать параметр explicit = true в solve, чтобы получить выражения переменных через свободные параметры, что упрощает анализ решения.

Для проверки решения рекомендуется подставить полученные значения обратно в исходные уравнения через оператор eval или функцию subs.

Если система содержит уравнения с параметрами, можно определить условия существования решений, используя пакет Student[LinearAlgebra] и функцию LinearSolve для линейных систем с параметрами.

Для работы с большими системами и получения всех решений рекомендуется предварительно упростить уравнения с помощью simplify или expand перед вызовом solve.

Анализ и проверка полученных решений в Maple

После получения решений уравнения в Maple важно выполнить их проверку на корректность и полноту. Для этого используйте команду subs, подставляя найденные корни обратно в исходное уравнение. Если результат равен нулю или упрощается до тождества, решение верно.

Команда simplify помогает упростить выражения и выявить скрытые ошибки, особенно если корни представлены в сложной форме. Рекомендуется применять simplify к обеим частям уравнения с подстановкой корней для подтверждения равенства.

Для систем уравнений используйте функцию isolate для выделения переменных и облегчения проверки каждой составляющей. Это особенно эффективно при работе с параметрическими решениями.

Для численных решений применяется команда evalf, позволяющая оценить точность корней и выявить возможные приближённые значения, что особенно важно при работе с уравнениями, не имеющими точных аналитических решений.

Если уравнение содержит параметры, используйте assume для задания условий, влияющих на корректность решения, и повторно запускайте проверку подставленных значений с учётом этих ограничений.

Для анализа кратности корней полезна команда RootFinding[Isolate], которая позволяет выделить все корни и определить их кратность, обеспечивая полный учёт всех вариантов решений.

Дополнительно можно применять функцию fsolve с различными диапазонами поиска, чтобы удостовериться, что не пропущены корни вне стандартного интервала.

Экспорт результатов решения уравнений из Maple в разные форматы

Maple предоставляет несколько удобных вариантов для экспорта результатов решения уравнений в различные форматы. Эти функции полезны для дальнейшей работы с результатами в других приложениях или для сохранения в нужном виде. Рассмотрим основные способы экспорта.

• Экспорт в текстовый формат (.txt): Для того чтобы экспортировать результат в текстовый файл, необходимо использовать команду fwrite или вручную сохранить результат через интерфейс программы. Для этого:
  • Для сохранения в файл выбирается пункт «File» → «Save As…» и выбирается формат .txt.
• Экспорт в формат LaTeX: Этот формат идеально подходит для математических формул, так как LaTeX используется для их качественного отображения.
  • В Maple используйте команду latex() для преобразования решения в формат LaTeX.
  • Например: latex(решение) сгенерирует код, который можно вставить в LaTeX-документ.
• Экспорт в PDF: Для создания отчетов или публикаций можно экспортировать результат в PDF.
  • Для этого выберите пункт «File» → «Print Preview» или «Export As» и затем выберите формат PDF.
  • Maple сохранит всю рабочую область, включая графику и текст, в PDF-файл.
• Экспорт в формат Excel (.xls, .xlsx): Если результат включает таблицы или числовые данные, экспорт в Excel позволяет удобно работать с ними в дальнейшем.
  • Для этого используйте команду Export[Excel](filename).
  • После выполнения команды результат будет сохранен в файл Excel, который можно открыть в Microsoft Excel или аналогичных приложениях.
• Экспорт в формат Maple Worksheet (.mw): Если нужно сохранить весь рабочий процесс для дальнейшего редактирования в Maple, используйте формат Maple Worksheet.
  • Для этого выберите «File» → «Save As…» и сохраните файл в формате .mw.

Кроме того, Maple позволяет экспортировать графику и математические объекты в форматы .png, .jpg и .bmp, что удобно для визуальных отчетов или презентаций.

Вопрос-ответ:

Как в Maple решить простое линейное уравнение?

Для решения простого линейного уравнения в Maple необходимо воспользоваться командой `solve`. Например, чтобы решить уравнение \(2x + 3 = 7\), нужно ввести команду: `solve(2*x + 3 = 7, x)`. Maple автоматически найдет значение переменной \(x\), которое удовлетворяет уравнению. Ответ будет \(x = 2\).

Что делать, если уравнение в Maple имеет несколько решений?

Когда уравнение имеет несколько решений, Maple выведет все возможные значения переменной. Например, для уравнения \(x^2 — 4 = 0\), команда `solve(x^2 — 4 = 0, x)` даст два решения: \(x = -2\) и \(x = 2\). Если уравнение имеет бесконечное количество решений, Maple также может вывести общий вид решений, например, для линейных уравнений с параметрами.

Как решить систему уравнений в Maple?

Для решения системы уравнений в Maple используется команда `solve` с указанием нескольких уравнений. Например, чтобы решить систему \(x + y = 5\) и \(x — y = 1\), нужно ввести команду: `solve({x + y = 5, x — y = 1}, {x, y})`. Maple автоматически найдет значения для \(x\) и \(y\), в данном случае ответ будет \(x = 3\), \(y = 2\).

Как в Maple решить нелинейное уравнение, например, с тригонометрическими функциями?

Для решения нелинейных уравнений, например, с тригонометрическими функциями, также используется команда `solve`. Например, чтобы решить уравнение \(\sin(x) = 0.5\), введите команду: `solve(sin(x) = 0.5, x)`. Maple предоставит все возможные решения в зависимости от диапазона значений, если это нужно, можно указать дополнительный параметр для ограничения решения в определённом интервале, например, от 0 до \(2\pi\).