Система компьютерной алгебры Maple предоставляет два подхода к вычислению интегралов: использование встроенных команд и пошаговое выполнение операций вручную. Оба метода применимы в учебных и научных целях, но требуют разных стратегий работы с выражениями. Автоматический расчет выполняется через команду int(), которая поддерживает определённые и неопределённые интегралы, а также обрабатывает рациональные, тригонометрические, экспоненциальные и даже специальные функции.
Например, вызов int(sin(x)^2, x) немедленно возвращает результат x/2 — sin(2x)/4. В случае определённого интеграла int(exp(-x^2), x = -infinity..infinity) Maple распознаёт функцию как Гауссову и возвращает точное значение sqrt(Pi). Однако не все интегралы решаются напрямую. При отсутствии замкнутой формы Maple возвращает выражение в виде int(), что сигнализирует о необходимости ручной доработки.
Ручное вычисление реализуется через команду Student[Calculus1], где доступны шаги упрощения, замены переменных, интегрирования по частям. Например, функция Student[Calculus1][Change] позволяет явно задать замену переменной, после чего Maple пошагово отображает преобразование. Это особенно полезно при обучении и проверке логики преобразований.
Как задать неопределённый интеграл вручную в Maple
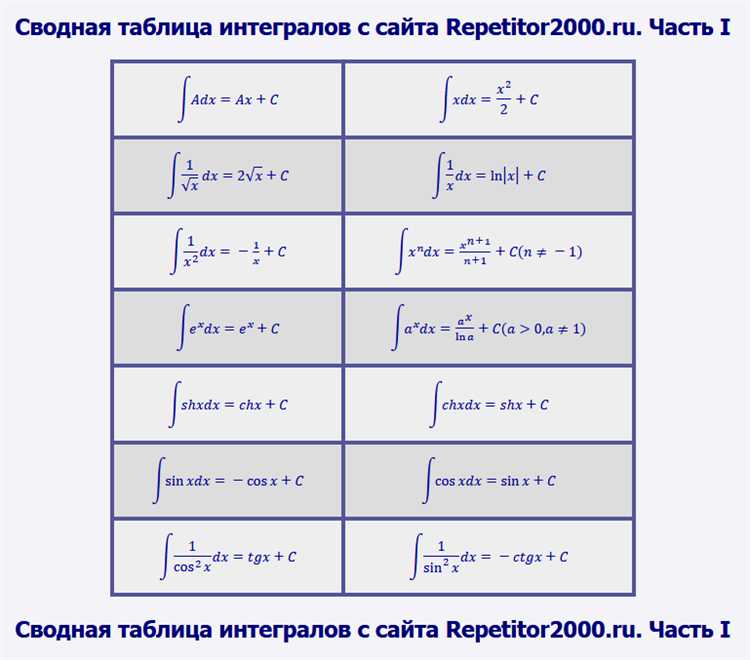
Для вычисления неопределённого интеграла в Maple используется функция int. Синтаксис следующий:
int(выражение, переменная)
Пример: чтобы вычислить интеграл от sin(x) по переменной x, введите:
int(sin(x), x);
Maple автоматически выполнит интегрирование и отобразит результат -cos(x). Чтобы получить только аналитическое выражение без его вычисления, используйте команду Int с заглавной буквы:
Int(sin(x), x);
Для отображения результата в виде математического выражения в двумерной записи используйте интерфейс Math Input или переключитесь на режим 2D Math через меню View → Mathematical Input.
Если переменная интегрирования не указана, Maple вернёт ошибку. Пример неправильного ввода:
int(sin(x));
Для интегралов по составным выражениям, например x*exp(x^2), используйте тот же синтаксис:
int(x*exp(x^2), x);
value(Int(exp(-x^2), x));
При работе с функциями нескольких переменных необходимо чётко указывать переменную интегрирования. Пример:
int(x*y^2, y); даст результат (1/3)*x*y^3.
Для проверки результата используйте команду diff. Пример:
diff(int(sin(x), x), x);
Если результат – исходная подынтегральная функция, интеграл вычислен корректно.
Ввод определённого интеграла с пределами через командную строку
В Maple для вычисления определённого интеграла используется команда int с обязательным указанием функции, переменной интегрирования и пределов. Формат ввода интеграла с пределами:
int(выражение, переменная = нижний_предел..верхний_предел)
Пример ввода определённого интеграла функции sin(x) от 0 до π:
int(sin(x), x=0..Pi);
Ключевые рекомендации при вводе интегралов в командной строке Maple:
- Пределы интегрирования указываются через двойную точку
.., а не через запятую или двоеточие. - Переменная интегрирования после запятой пишется с указанием диапазона в виде
переменная=нижний_предел..верхний_предел, без пробелов. - Константы и специальные значения, например, π, пишутся с большой буквы
Piи без кавычек. - При работе с неопределёнными символами или параметрами их необходимо объявлять заранее или использовать команду
assume. - Если пределы содержат выражения, их нужно вводить как математические формулы, например,
int(x^2, x=1..a+1). - Для вычисления интеграла с несколькими переменными указывайте пределы для каждой переменной отдельно внутри одной команды.
Ввод через командную строку позволяет оперативно задавать интегралы и сразу получать результат или выражение для дальнейших вычислений. Ошибки часто связаны с неправильным синтаксисом пределов или отсутствием точки между ними.
Использование команды int для ручного вычисления интегралов
Команда int в Maple предназначена для вычисления определённых и неопределённых интегралов с точным указанием выражения и переменной интегрирования. Синтаксис базируется на форме int(выражение, переменная) для неопределённого интеграла и int(выражение, переменная = предел_нижний..предел_верхний) для определённого.
Для ручного контроля вычисления необходимо строго задавать переменную интегрирования и, при необходимости, границы интеграла. Важно избегать автоматического упрощения, если требуется пошаговое решение – для этого можно использовать опцию method, указывающую конкретный способ интегрирования.
Пример вычисления неопределённого интеграла вручную: int(sin(x)^2, x); – Maple вернёт точное аналитическое выражение. Для определённого интеграла с границами: int(exp(-x^2), x = 0..1); – команда вычислит значение с помощью встроенных методов численного интегрирования, если аналитическое выражение отсутствует.
В случаях, когда требуется получить результат в более удобном виде, можно использовать дополнительные команды simplify или expand после вычисления интеграла. Для сложных выражений рекомендуется разбивать интеграл на части и вычислять их по отдельности, что повышает точность и контроль над процессом.
Ручное использование int требует чёткого понимания структуры интегрируемого выражения и корректного задания пределов. Для работы с параметрами и сложными функциями следует явно указывать все переменные и параметры, чтобы избежать неоднозначностей в вычислении.
Применение меню Maple для автоматического интегрирования

Maple предоставляет удобный графический интерфейс для быстрого вычисления интегралов с помощью встроенного меню. Для автоматического интегрирования необходимо выделить выражение в рабочей области, после чего выбрать в верхнем меню пункт Calculus, затем Integrate. В открывшемся подменю доступны варианты: неопределённый интеграл, определённый интеграл с вводом границ интегрирования и численное интегрирование.
Для неопределённого интеграла система автоматически предложит результат с учётом константы интегрирования. При вычислении определённого интеграла следует указать пределы интегрирования в появившихся полях. Maple сразу вычислит результат и подставит его в рабочую область без необходимости писать отдельные команды.
Меню позволяет выбрать интегрирование по конкретной переменной, если в выражении присутствуют несколько переменных. Это полезно при работе с многомерными функциями, где требуется интегрировать последовательно по разным переменным.
В случае численного интегрирования меню предлагает опции для задания точности и метода интегрирования, например, метод Симпсона или Квадратурные формулы. Эти параметры изменяются через дополнительное диалоговое окно, которое открывается после выбора численного интеграла.
Использование меню Maple особенно эффективно при необходимости быстрого получения результата без написания кода. Для сложных выражений меню поддерживает интегрирование с параметрами и дополнительными ограничениями, что значительно облегчает анализ задачи.
Решение интегралов с параметрами и переменными
При вычислении интегралов с параметрами и переменными в Maple важно четко задать область определения и тип параметров. Для символического интегрирования следует использовать команду int, указывая переменную интегрирования и параметры как символы без численных значений.
Если параметры присутствуют в интегранде, Maple автоматически учитывает их при вычислении первообразной, возвращая выражение, включающее эти параметры. В случае неопределенных параметров рекомендуется использовать опцию assume для ограничения их области (например, положительность), что влияет на вид результата и упрощает его.
Для численного интегрирования с параметрами применяется функция evalf(Int(...)) или команда evalf(int(...)) с подстановкой конкретных значений параметров через subs. Такой подход обеспечивает гибкость в исследовании зависимости интеграла от параметров.
Особенности работы с параметрами проявляются при вычислении интегралов с переменными верхними и нижними пределами, где интеграл становится функцией параметра. Maple поддерживает дифференцирование таких интегралов по параметру через оператор D или команду diff, что позволяет анализировать их поведение.
При сложных выражениях рекомендуется разбивать интеграл на части и поэтапно вычислять каждый элемент с параметрами. Также полезно применять упрощения через simplify и factor для получения более компактных результатов.
Обработка разрывов и особенностей подынтегральной функции
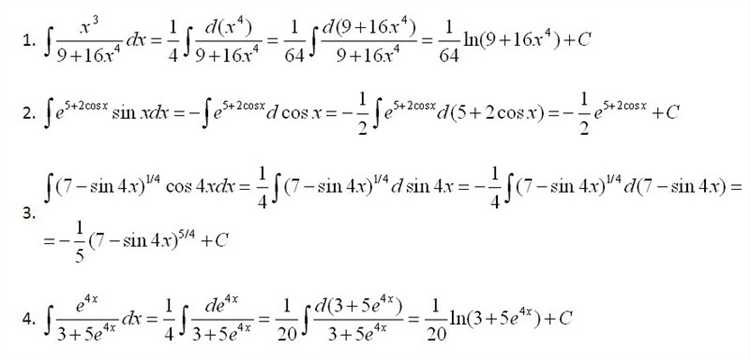
При вычислении интегралов в Maple важна предварительная проверка функции на наличие разрывов и особенностей, таких как точки разрыва второго рода, полюса или точек разветвления. Для этого применяется команда singularities(f(x), x), позволяющая выявить критические значения переменной.
Автоматический интегратор Maple корректно работает с большинством точек особенностей, но в случаях существенных разрывов интеграл может не существовать в классическом смысле. Рекомендуется разделять интеграл по промежуткам, избегая точек разрыва, и использовать понятие несобственного интеграла с ограничением на пределы интегрирования.
Для ручного контроля допускается предварительное вычисление пределов функции около особенностей с помощью limit(f(x), x=a, dir), где a – точка разрыва, а dir – направление предела (справа или слева). Если пределы конечны и совпадают, интегрирование в данной точке можно считать корректным.
В случае обнаружения особенностей, влияющих на интегрируемость, можно использовать разбиение интервала интегрирования и вычислять интеграл по частям, применяя int(f(x), x, a, c) + int(f(x), x, c, b), где c – точка разрыва. Для несобственных интегралов задаётся предел с помощью limit(int(f(x), x, a, t), t->c).
Также Maple поддерживает функцию PrincipalValue для вычисления главного значения интеграла при наличии особенностей, связанных с интегрированием по сингулярным точкам. Использование этого подхода необходимо при интегрировании с полюсами внутри интервала.
Для функций с особым поведением рекомендуется анализировать свойства подынтегрального выражения, например, путем разложения в ряд Тейлора или Лорана в окрестности точек разрыва, что позволяет выявить характер особенностей и подобрать оптимальный метод интегрирования.
Оптимальная практика – комбинировать оба подхода: автоматически получить итоговый результат, а затем вручную проверить ключевые этапы вычисления, используя функционал Maple для разложения и упрощения. Это повышает надёжность решения и помогает выявить скрытые особенности исходного выражения.
Сохранение и экспорт результатов интегрирования в разные форматы
В Maple результаты вычисления интегралов можно сохранить и экспортировать в различных форматах для дальнейшего использования в документах, отчетах или презентациях. Для этого предусмотрены как встроенные команды, так и графический интерфейс.
Основные форматы сохранения результатов интегрирования:
- Maple Worksheet (*.mw) – сохраняет полный рабочий файл с исходным кодом и результатами, поддерживает интерактивность.
- Maple Input (*.mpl) – сохраняет только исходные команды без результатов, удобно для передачи кода.
- MathML и LaTeX – для экспорта математических выражений в форматах, используемых в веб-страницах и научных статьях.
- PDF и HTML – для публикации готовых отчетов и обмена результатами в читаемом виде.
Рекомендуемые команды для экспорта интегралов:
save(filename)– сохраняет весь текущий рабочий лист в формате *.mw.TextTools:-Export(filename, expression)– экспортирует конкретное выражение в текстовый файл.latex(expression)– генерирует LaTeX-код для результата интегрирования.Export(filename, expression, format)– универсальная команда для сохранения в форматах MathML, PDF, HTML.
Для сохранения результата интегрирования в LaTeX, например, используется команда:
latex(Int(f(x), x));
Полученный код можно вставить в научную публикацию без потери форматирования. При экспорте в MathML целесообразно использовать:
Export("result.mathml", Int(f(x), x), "MathML");
Для автоматизации сохранения в PDF или HTML стоит применять команду:
Export("report.pdf", plot(Int(f(x), x)), "PDF");
где можно указать конкретные элементы (текст, графики) для экспорта.
Рекомендации по организации процесса:
- Для сохранения промежуточных результатов используйте функции
saveиreadдля восстановления сеанса. - Экспортируйте только необходимые выражения, избегая сохранения лишних данных, чтобы не перегружать файлы.
- Используйте LaTeX-экспорт для интегралов, включаемых в научные статьи, поскольку формат обеспечивает корректное отображение сложных формул.
- При экспорте в HTML или PDF для презентаций контролируйте форматирование с помощью встроенных настроек Maple.
Вопрос-ответ:
Как в Maple выполнить вычисление интеграла вручную и чем это отличается от автоматического способа?
В Maple есть два основных подхода к вычислению интегралов. Вручную пользователь вводит команды, используя конкретные методы, например, разложение по частям или подстановку, задавая шаги вычисления самостоятельно. Автоматический режим позволяет программе самой выбрать способ интегрирования и вычислить результат без вмешательства. Вручной подход полезен для обучения и понимания процесса, тогда как автоматический значительно экономит время при стандартных задачах.
Можно ли в Maple вычислять интегралы с параметрами и как это делается?
Да, Maple поддерживает интегрирование выражений с параметрами. Для этого достаточно указать параметр в формуле интеграла, и программа обработает его символически. При этом можно получить результат, выраженный через параметры, что удобно для дальнейшего анализа. Иногда Maple может выдать общий вид решения с условием на параметры, либо потребовать дополнительных предположений.
Какие типичные ошибки возникают при вычислении интегралов в Maple и как их избежать?
Часто встречаются ошибки, связанные с неверным вводом выражения, пропуском знаков или неправильным указанием переменной интегрирования. Также иногда Maple не может найти первообразную из-за слишком сложной функции или требует дополнительных предположений. Чтобы избежать проблем, нужно внимательно проверять синтаксис, правильно указывать переменные, а при необходимости использовать вспомогательные команды для упрощения выражения.
Можно ли в Maple получить пошаговое решение интеграла и каким образом это активируется?
В Maple предусмотрена возможность просмотра промежуточных шагов решения интеграла. Для этого применяются специальные пакеты или команды, например, Student[Calculus1]:IntegralStepByStep(). Они показывают отдельные этапы вычисления, такие как разбиение на части, замена переменной, интегрирование каждого слагаемого. Этот режим удобен для изучения и проверки своих действий при решении.
Как Maple справляется с вычислением сложных интегралов, включающих специальные функции или параметры?
Maple обладает мощными алгоритмами для работы с интегралами, в том числе с теми, которые содержат специальные функции (гамма, бета, гипергеометрические и др.). В таких случаях программа может выразить результат через известные специальные функции или предоставить численное приближение. Если аналитическое выражение сложно получить, Maple предложит численные методы интегрирования для точного вычисления значения.
Какие способы вычисления интегралов доступны в Maple и как выбрать между ручным и автоматическим методом?
В Maple интегралы можно вычислять двумя основными способами: вручную, используя команды для пошагового разложения и преобразования, и автоматически — с помощью встроенных функций, которые рассчитывают результат без участия пользователя. Ручной метод подходит, если нужно понять ход решения, проверить промежуточные шаги или использовать специфические приёмы преобразования. Автоматический — удобен для быстрого получения ответа, особенно при сложных выражениях. Выбор зависит от целей: если важна обучающая составляющая, стоит работать вручную, а если нужно лишь итоговое значение — автоматический метод.
Как в Maple можно проверить правильность найденного интеграла и какие ошибки часто встречаются при автоматическом вычислении?
Проверить результат интегрирования в Maple можно, взяв производную от найденного первообразного и сравнив её с подынтегральной функцией. Если они совпадают, ответ корректен. Ошибки при автоматическом вычислении встречаются редко, но могут возникать при наличии разрывов, особенностей или сложных функций, которые Maple интерпретирует не так, как ожидает пользователь. В таких случаях полезно использовать ручное вычисление с пошаговыми командами, чтобы выявить, на каком этапе возникает проблема, или попробовать альтернативные подходы к интегрированию.