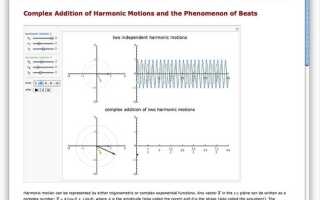
Wolfram Mathematica предлагает встроенную функцию Limit, которая позволяет находить пределы сложных выражений в нескольких кликах. Для быстрого результата важно корректно задавать переменную и точку стремления, используя синтаксис Limit[функция, переменная → точка].
Для пределов, стремящихся к бесконечности, достаточно указать ∞ или -∞, например: Limit[Sin[x]/x, x → ∞]. Если нужно рассчитать односторонний предел, стоит добавить направление с помощью Direction -> 1 или Direction -> -1.
Оптимизация скорости вычислений достигается упрощением выражений перед применением Limit, а также использованием опции Assumptions для уточнения условий переменной. Это уменьшает вероятность ошибок и ускоряет получение точного результата.
Использование функции Limit для вычисления пределов в точке
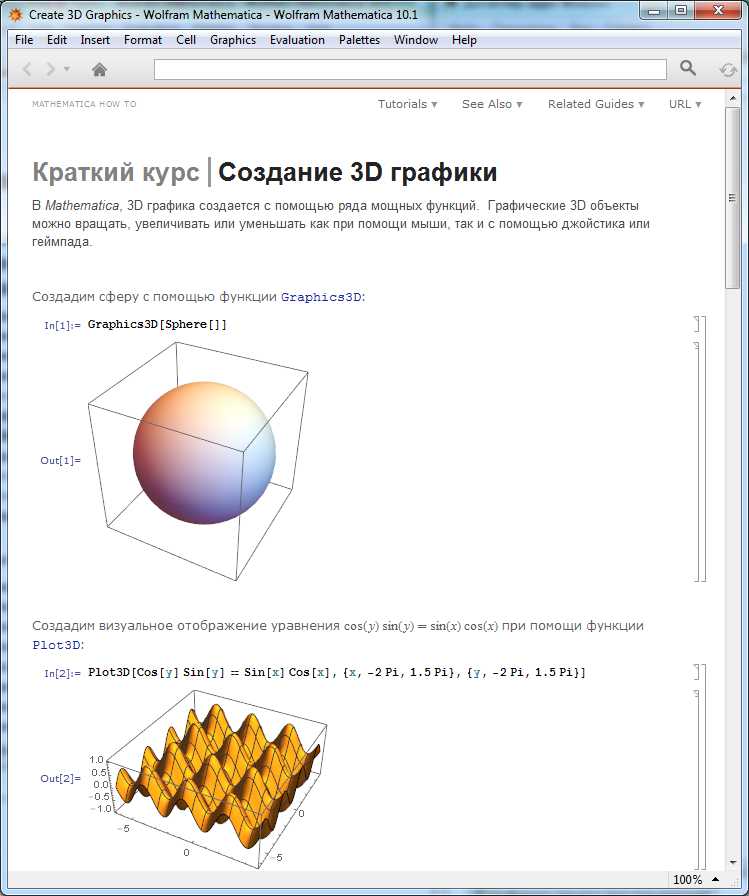
Функция Limit в Wolfram Mathematica предназначена для точного вычисления пределов функции при стремлении переменной к заданному значению. Синтаксис базовой команды выглядит так: Limit[выражение, переменная -> точка]. Например, Limit[Sin[x]/x, x -> 0] вычислит предел выражения Sin(x)/x при x, стремящемся к 0.
Для корректного результата важно задать переменную и значение, к которому она стремится, используя стрелку ->. При необходимости можно указать направление предела: справа или слева, добавив третий аргумент Limit[выражение, x -> a, Direction -> «FromAbove»] или Direction -> «FromBelow». Это полезно при разрывах и односторонних пределах.
Функция поддерживает вычисление пределов с бесконечностью: Limit[1/x, x -> Infinity] вернёт 0, а при стремлении к минус бесконечности аналогично.
Для ускорения вычислений рекомендуется предварительно упростить выражение с помощью Simplify или FullSimplify, что снижает нагрузку на движок пределов и помогает избежать неопределённостей.
Если результат не удаётся получить напрямую, можно использовать Assuming для задания условий, например, о знаке переменной, что часто влияет на односторонние пределы.
Для численных приближений предела существует функция NSolve и FindRoot, но в случае пределов предпочтительнее именно Limit, так как она даёт точный аналитический ответ.
Вычисление односторонних пределов с помощью Mathematica
Для вычисления односторонних пределов в Wolfram Mathematica используется функция Limit с дополнительным параметром Direction. Этот параметр принимает значения 1 для предела справа (x → a⁺) и -1 для предела слева (x → a⁻).
Синтаксис выглядит так: Limit[f[x], x → a, Direction -> 1] для правостороннего предела и Limit[f[x], x → a, Direction -> -1] для левостороннего.
Например, для функции f(x) = 1/(x - 2) при приближении к 2 справа следует написать Limit[1/(x - 2), x -> 2, Direction -> 1], что даст бесконечность, а при подходе слева – Limit[1/(x - 2), x -> 2, Direction -> -1], результат будет минус бесконечность.
Если односторонний предел не существует, Mathematica вернёт выражение с Limit, что означает необходимость перепроверки функции или области определения.
Для ускорения вычислений стоит использовать упрощение функции до вызова предела, например через Simplify или FullSimplify. Это часто уменьшает время и повышает точность результата.
Важно помнить, что Limit учитывает направление только при указании параметра Direction. Без него вычисляется обычный двухсторонний предел, что может привести к ошибкам при разрывах или неоднозначных значениях.
Автоматическое определение пределов бесконечных выражений
Wolfram Mathematica имеет встроенную функцию Limit, способную автоматически вычислять пределы, включая случаи с бесконечными значениями переменных и выражений. Для определения предела при стремлении переменной к бесконечности используется синтаксис:
Limit[выражение, переменная -> Infinity]
Аналогично, пределы при стремлении к минус бесконечности задаются через Limit[выражение, переменная -> -Infinity]. Mathematica анализирует поведение функции, автоматически выбирая методы упрощения и раскрытия неопределенностей, что позволяет получать точный результат без дополнительного вмешательства.
Если выражение содержит неопределённости вида ∞/∞ или 0·∞, рекомендуется использовать опцию Assumptions для уточнения условий переменной. Например:
Limit[выражение, переменная -> Infinity, Assumptions -> переменная > 0]
Для ускорения вычислений при сложных выражениях можно задать параметр GenerateConditions -> False, чтобы исключить проверку условий существования предела. Это полезно, когда важен лишь числовой результат.
Mathematica также автоматически обрабатывает пределы функций с экспонентами, логарифмами и тригонометрическими выражениями, распознавая тип бесконечности и применяя разложение по Тейлору или правило Лопиталя при необходимости.
Для проверки правильности результата стоит использовать численное приближение функции при больших значениях переменной, например, вычисляя значения функции при x = 10^6, 10^7. Если численные значения сходятся к пределу, результат корректен.
Работа с параметрическими пределами и их вычисление
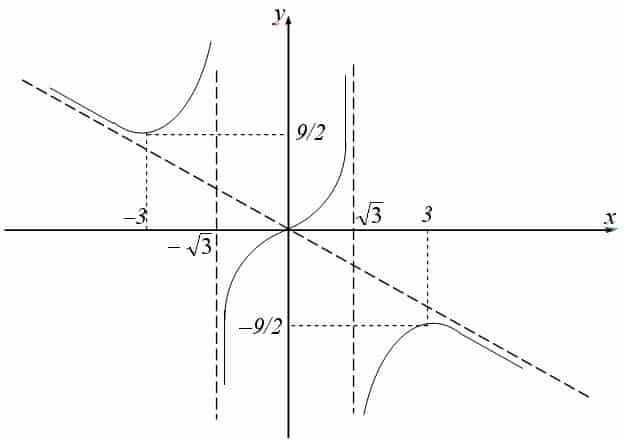
В Wolfram Mathematica вычисление пределов с параметрами удобно реализуется через функцию Limit с использованием синтаксиса Limit[expr, {x -> a, Assumptions -> conditions}]. Это позволяет явно задать ограничения на параметры, влияющие на поведение функции при приближении переменной.
Для анализа пределов, зависящих от параметра, важно использовать опцию Assumptions или условие в вызове функции Simplify вместе с Limit. Например, Limit[f[x, α], x -> 0, Assumptions -> α > 0] даст результат при положительных значениях параметра.
При наличии нескольких параметров можно комбинировать условия, например, Assumptions -> α > 0 && β < 1. Это гарантирует корректность результата при конкретных параметрических ограничениях.
Если предел зависит от параметра, и требуется получить общую формулу, используется Limit без явных условий с последующим упрощением результата через Simplify или FullSimplify с указанными предположениями.
Для вычисления односторонних пределов параметрических функций применяются опции Direction -> 1 (справа) или Direction -> -1 (слева) внутри Limit. Это важно при исследовании разрывов, зависящих от параметров.
Если параметр задает порядок стремления переменной к бесконечности или нулю, следует использовать предельные переходы с помощью Limit[expr, {x -> ∞}] и дополнительно фиксировать диапазон параметров для предотвращения неопределенностей.
В сложных случаях, когда автоматическое вычисление предела невозможно, рекомендуется разложить выражение с помощью Series, затем выделить главный член и вычислить предел от упрощённой формы.
Обработка неопределённостей при вычислении пределов
В Wolfram Mathematica неопределённости типа 0/0, ∞/∞ и другие возникают часто при вычислении пределов. Для их корректной обработки применяют специальные приёмы и функции.
- Использование функции Limit с опцией Assumptions:
Задавая дополнительные условия, можно уточнить поведение функции рядом с точкой, что снижает риск неопределённостей.
- Применение правил Лопиталя:
- Mathematica автоматически применяет правила Лопиталя при вычислении пределов с неопределённостями.
- Если автоматическая обработка не сработала, можно вручную дифференцировать числитель и знаменатель и вычислить предел заново.
- Преобразование выражений:
- Приведение функции к удобному виду (разложение в ряд Тейлора, факторизация) помогает избежать неопределённостей.
- Команда Series позволяет разложить функцию в окрестности точки и проанализировать старшие члены.
- Использование функций Simplify и FullSimplify:
Иногда неопределённости связаны с неявными сокращениями; упрощение выражения перед вычислением предела помогает устранить их.
При возникновении неопределённости рекомендуется последовательно:
- Проверить исходное выражение на возможность упрощения.
- Использовать Series для анализа локального поведения.
- При необходимости вручную применить правило Лопиталя.
- Уточнить условия вычисления через Assumptions в Limit.
Такой подход обеспечивает точность и ускоряет получение результата без лишних вычислительных затрат.
Настройка точности и времени вычислений в Limit
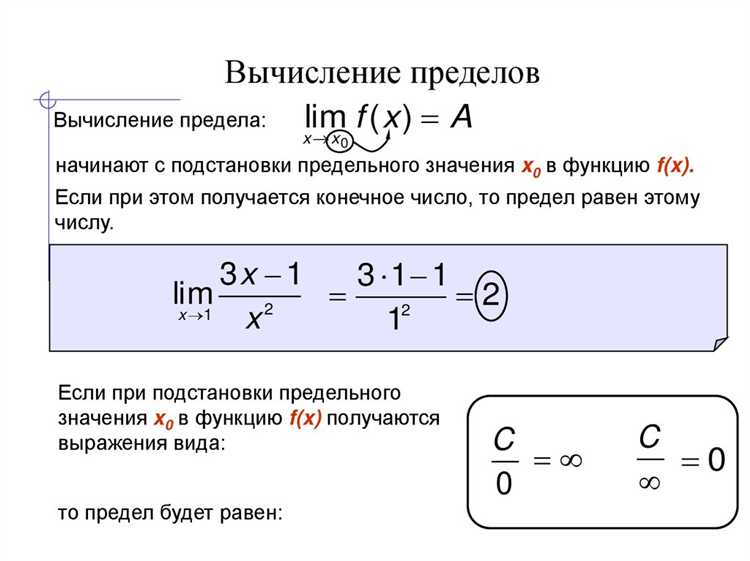
В Wolfram Mathematica функция Limit по умолчанию использует внутренние алгоритмы с автоматической точностью. Для контроля точности можно применять опцию WorkingPrecision, задавая количество знаков после запятой. Например, Limit[f[x], x -> a, WorkingPrecision -> 30] увеличит точность вычислений до 30 знаков, что полезно при работе с выражениями, чувствительными к округлениям.
Если вычисление занимает слишком много времени, стоит ограничить время работы с помощью функции TimeConstrained. Например, TimeConstrained[Limit[f[x], x -> a], 5] прервет вычисление, если оно длится более 5 секунд, что предотвращает зависание при сложных выражениях.
В некоторых случаях помогает настройка опций Method и MaxIterations. Например, Limit[f[x], x -> a, Method -> "Heuristic", MaxIterations -> 100] ограничит количество итераций и выберет приближенный метод для ускорения результата.
Для численных пределов стоит использовать NumericalLimit из пакета NumericalCalculus`, который позволяет гибко управлять точностью и количеством шагов.
Рекомендуется начинать с базовых вызовов Limit и добавлять опции по мере необходимости, учитывая баланс между точностью и временем вычислений.
Вопрос-ответ:
Какие команды в Wolfram Mathematica подходят для вычисления пределов функций?
Для вычисления пределов в Mathematica чаще всего используют функцию Limit. Она позволяет указать выражение, переменную и точку, к которой стремится переменная. Например, Limit[f[x], x -> a] вычисляет предел функции f при x, стремящемся к a. Также можно задавать дополнительные параметры для односторонних пределов.
Как задать односторонний предел в Wolfram Mathematica?
Чтобы вычислить односторонний предел, в функции Limit нужно указать направление предела с помощью третьего аргумента. Например, Limit[f[x], x -> a, Direction -> 1] вычисляет предел при x, стремящемся к a справа, а Direction -> -1 — слева. Это полезно, когда функция ведет себя по-разному с разных сторон точки.
Можно ли в Mathematica быстро получить пределы сложных выражений с параметрами?
Да, Mathematica хорошо справляется с вычислением пределов даже для выражений, содержащих параметры и несколько переменных. Можно использовать Limit с подстановками и упрощениями. В некоторых случаях удобно предварительно упростить выражение через Simplify или FullSimplify, чтобы ускорить вычисление предела.
Как проверить корректность результата предела, вычисленного в Mathematica?
Для проверки можно построить график функции рядом с точкой, где берется предел, и визуально оценить поведение. Также можно подставить значения переменной, близкие к точке, и сравнить численные значения с результатом функции Limit. Такой подход помогает убедиться, что вычисление прошло верно.
Можно ли автоматизировать вычисление пределов для большого количества функций в Mathematica?
Да, можно написать цикл или использовать функции Map и Table, чтобы вычислять пределы для списка выражений. Например, Limit /@ список_функций быстро выдаст пределы по заданной переменной и точке. Это удобно при анализе серии функций без ручного ввода каждого варианта.